Математика/5. Математическое моделирование
Д.ф.-м.н. Джайчибеков
Н.Ж.
Евразийский национальный
университет им.Л.Н.Гумилева, Казахстан
Д.ф.-м.н. Матвеев С.К.
Санкт-Петербургский
государственный университет, Россия
Решение задачи о структуре ударной волны
для конечных чисел Маха
В [1-3] рассмотрено применение в динамике
разреженного газа эвристической модели течения, ранее разработанной для
описания течения газа с твердыми частицами [4]. В этой модели молекулы
подразделяются на 2 множества, каждое
из которых описывается континуально, причем столкновения молекул из одного
множества порождают напряжения и тепловые потоки в этом множестве, а
столкновения молекул разных множеств приводят к переходу частиц из одного
множества в другое. В указанных работах частицы одного из множеств (назовем их s-частицами)
двигались упорядоченно без хаотической составляющей скорости и естественно, что
все столкновения таких частиц с частицами другого множества (t-частицами)
приводили к переходу s-частиц
в множество хаотически движущихся t-частиц.
Достоинством этой модели является ее простота,
поскольку легко подсчитать массу, импульс и энергию, переносимые частицами при
таком переходе, и не требуется никаких характеристик взаимодействия частиц,
кроме частоты столкновений. Применение этой модели к расчету структуры скачка
уплотнения [1] и обтекания сферы разреженным газом [2,3] показало
удовлетворительную точность.
Предположение, что s-частицы движутся
упорядоченно (с пренебрежимо малой хаотической составляющей скорости), ограничивает
применение модели случаем гиперзвукового течения газа. В настоящей работе
дается обобщение описанной модели на случай, когда частицы обоих множеств имеют
хаотическую составляющую скорости, это дает возможность использовать модель при
любых числах Маха.
Как и раньше будем считать молекулы твердыми
абсолютно упругими сферами и по-прежнему будем считать, что при любом
столкновении частиц из разных множеств, происходит переход частицы из одного
множества в другое. В каждом из множеств будем считать распределение частиц по
скоростям близким к максвелловскому и в соответствии с этим определять
напряжения и тепловые потоки. Однако, если раньше было естественно считать, что
упорядоченно движущиеся s-частицы
после столкновений переходят в множество хаотически движущихся t-частиц, то теперь в
случае, когда в обоих множествах есть хаотическое движение, будем считать
вероятным и переход t-частиц
в множество s-частиц. Обозначим ![]() вероятность при
столкновении s-частицы перейти в
множество t-частиц, а вероятность t-частицы перейти в
множество s-частиц, соответственно,
вероятность при
столкновении s-частицы перейти в
множество t-частиц, а вероятность t-частицы перейти в
множество s-частиц, соответственно,
![]() .
.
Вероятность перехода частиц из одного множества
в другое естественно связать с интенсивностью хаотического движения частиц в
соответствующем множестве, причем больше вероятность перехода в то множество, в
котором больше интенсивность хаотического движения. Эту интенсивность можно
характеризовать средним модулем скорости хаотического движения ![]() , где p
– давление,
, где p
– давление, ![]() – плотность i-го
газа (i=s,t),
– плотность i-го
газа (i=s,t), ![]() – показатель
адиабаты, причем
– показатель
адиабаты, причем ![]() = 5/3, если вращение частиц не учитывается, и
= 5/3, если вращение частиц не учитывается, и ![]() = 4/3, если энергия хаотического движения равномерно
распределена по вращательным и поступательным степеням свободы.
= 4/3, если энергия хаотического движения равномерно
распределена по вращательным и поступательным степеням свободы.
Наиболее естественным является предположение,
что ![]() пропорционально
пропорционально ![]() , поскольку
, поскольку ![]() есть некоторый объем
в пространстве скоростей, характеризующий интенсивность хаотического движения
частиц, а
есть некоторый объем
в пространстве скоростей, характеризующий интенсивность хаотического движения
частиц, а ![]() есть вероятность
столкнувшейся частицы оказаться после столкновения в множестве t. Аналогично
есть вероятность
столкнувшейся частицы оказаться после столкновения в множестве t. Аналогично ![]() пропорционально
пропорционально ![]() , откуда следует
, откуда следует ![]() .
.
Рассмотрим теперь на
основе описанной модели структуру скачка уплотнения в газе, следуя [1], где это
сделано для случая гиперзвукового потока перед скачком. Уравнения баланса
массы, импульса и энергии для s- и t-компонентов
потока при континуальном описании имеют вид:
![]() ,
, ![]() , (1)
, (1)
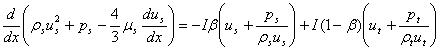 , (2)
, (2)
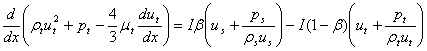 , (3)
, (3)
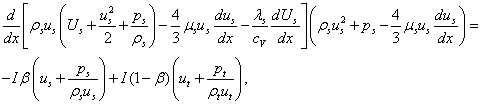 (4)
(4)
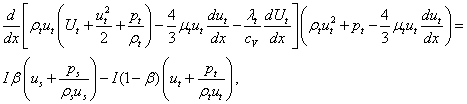 (5)
(5)
где ![]() - плотность и
скорость компонентов (индекс указывает соответствующий компонент),
- плотность и
скорость компонентов (индекс указывает соответствующий компонент), ![]() - кинетическая
энергия хаотического движения молекул,
- кинетическая
энергия хаотического движения молекул, ![]() - удельная
теплоемкость газа при постоянном объеме,
- удельная
теплоемкость газа при постоянном объеме, ![]() - масса молекул
одного множества, столкнувшихся с молекулами другого множества в единичном
объеме в единицу времени. Приближенно будем полагать
- масса молекул
одного множества, столкнувшихся с молекулами другого множества в единичном
объеме в единицу времени. Приближенно будем полагать
![]() . (6)
. (6)
Здесь
m – масса молекул, d – их диаметр; ![]() - вязкость и
теплопроводность компонентов, которые могут быть определены как для газа из
твердых сфер. Для каждого из компонентов считается справедливым уравнение
состояния
- вязкость и
теплопроводность компонентов, которые могут быть определены как для газа из
твердых сфер. Для каждого из компонентов считается справедливым уравнение
состояния
![]() , (7)
, (7)
Для расчета структуры скачка с
помощью приведенных уравнений сформулируем граничные условия:
при ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
и при ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Вследствие
сохранения массы, импульса и энергии потока должны выполняться условия
динамической совместности:
![]() ,
, ![]() ,
,
где
![]() - число Маха потока
перед скачком.
- число Маха потока
перед скачком.
В дальнейшем перейдем к
безразмерным переменным, взяв за масштабы скорости, плотности и длины
соответственно ![]() и сохранив прежние
обозначения.
и сохранив прежние
обозначения.
Сначала будем считать оба
компонента невязкими и нетеплопроводными, положив ![]() и
и ![]() . Тогда уравнения (1) – (5) можно записать в виде
. Тогда уравнения (1) – (5) можно записать в виде
![]() ,
, ![]() ;
(8)
;
(8)
![]() ,
, ![]() ; (9)
; (9)
![]() ,
, ![]() ; (10)
; (10)
где
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Складывая попарно уравнения (8), (9) и
(10), легко получить после интегрирования и определения констант из граничных
условий
![]() ,
, ![]() ,
, ![]() .
.
Из
решения уравнений (8 – 10) можно получить, что ![]() не зависят от x, постоянными также
являются
не зависят от x, постоянными также
являются ![]() и зависящие от них
и зависящие от них ![]() , а изменяются только
плотности компонент
, а изменяются только
плотности компонент ![]() и зависящие от них
и зависящие от них ![]() . Из первого уравнения (8) имеем
. Из первого уравнения (8) имеем ![]() , откуда, выбрав за начало отсчета x точку, где
, откуда, выбрав за начало отсчета x точку, где![]() , имеем
, имеем ![]() , а из второго уравнения (8) получим
, а из второго уравнения (8) получим ![]() . Здесь обозначено
. Здесь обозначено
![]()
![]()
То обстоятельство, что скорости и
внутренние энергии компонент в соответствии с полученным решением не зависят от
x, приводит к тому, что
их вязкость и теплопроводность не существенны и полученное решение справедливо
и для вязкого теплопроводного газа.
Литература:
1.
Матвеев С.К., Кочерыженков Г.В. Структура ударных волн в газах и газовзвесях. //
Сб. Динамические процессы в газах и твердых телах. Л., 1990. С. 28 – 36.
2.
Джайчибеков Н.Ж., Матвеев С.К. Применение трехкомпонентной модели к расчету
обтекания тел газовзвесью и разреженным газом. Журнал ПМТФ. СО АН СССР, Новосибирск, 1991,
№1, – С. 39-42.
3. Матвеев С.К., Джайчибеков Н.Ж. Расчет
обтекания сферы разреженным газом при произвольном числе Кнудсена. // Вестник Санкт-Петербургского университета. Санкт-Петербург.
1992. сер.1, вып.2. (№8) – С. 77-81.
4. Матвеев С.К. Математическое описание
обтекания тел потоком газовзвеси с учетом влияния отраженных частиц. // Сб.
Движение сжимаемых жидкостей и неоднородных сред. Л., 1982. Вып.7. С. 189 –
201.