Сведения об авторах

Рубен Степанович Геворкян − профессор, доктор

физ-мат. наук, ведущий научный сотрудник

института Механики НАН РА.

Тел.:       (37410) 270828,   (37493) 536883

e-mail:   gevorgyanrs@mail.ru

Дом. адрес:            ул. Киевяна 12, кв. 6.

                    0028, Ереван, Армения.

 

 

Aрмине Гамлетовна Саркисян

кандидат физ-мат. наук, старший научный сотрудник

института Механики НАН РА.

Тел.:   (37410) 610423,   (37477) 459033                 

e-mail:  armin.sa@bk.ru

Дом. адрес:         Аван, ул. Дуряна 32, кв. 51.

                   0044, Ереван, Армения.

 

 

 

 

 

 

 

 

 

 

 

УДК 536.21

                                Геворкян Р.С., Саркисян А.Г.

К ЗАДАЧЕ ТЕПЛОПРОВОДНОСТИ АНИЗОТРОПНЫХ В ПЛАНЕ НЕОДНОРОДНЫХ ТОРОИДАЛЬНЫХ ОБОЛОЧЕК   

Aсимптотическим интегрированием уравнений трехмерной задачи теории теплопроводности анизотропного неоднородного тела решены задачи для термически анизотропной в плане неоднородной тонкой тороидальной оболочки при различных граничных условиях. Выведены рекуррентные формулы для амплитуд тепловой волны, проведен анализ.

Тороидальные оболочки имеют широкое применение в технике и строительстве (тоннели, токамаки, ускорители). Определению напряженно-деформированного состояния тороидальных оболочек  посвящено много работ  [1], где задачи рассмотрены  в постановке классической теории оболочек. Учитывая  особенность геометрии тора [2]  (переменность знака  Гауссовой кривизны) и широкое распространение конструкций вида тороидальной оболочки, в работах [3,4] асимптотическим интегрированием уравнений трехмерной задачи теории термоупругости термически анизотропного неоднородного тела решены  несвязанные  статическая [3] и динамическая [4] задачи для тонкой тороидальной оболочки в предположении, что для такой оболочки имеется решение  соответствующей задачи теплопроводности. Для реализации вышеуказанного предположения, в предлагаемой работе решены задачи теплопроводности для анизотропной в плане неоднородной тонкой тороидальной оболочки при различных граничных условиях. Выведены рекуррентные формулы для амплитуд тепловой волны,  проведены примеры вместе с их анализом.        

1. Постановка краевых задач. Имеем  тороидальную оболочку, срединняя поверхность которой получена вращением образующей окружности радиуса  воокруг оси ОZ лежащей в плоскости окружности на расстоянии  от ее центра.

Пусть она в тороидальной системе координат занимает область:         

          На фигуре изображены тороидальная оболочка и ее поперечное сечение, где ось  направлена по внешней нормали к срединной поверхности оболочки, – угол между  и осю ОZ,  – угол поворота образующей окружности,  внешняя и внутренняя поверхности оболочки. Символами ,   обозначены области () и ()  поверхностей , имеющие соответственно  положительную  и  отрицателжную  гауссовые кривизны.

 

 

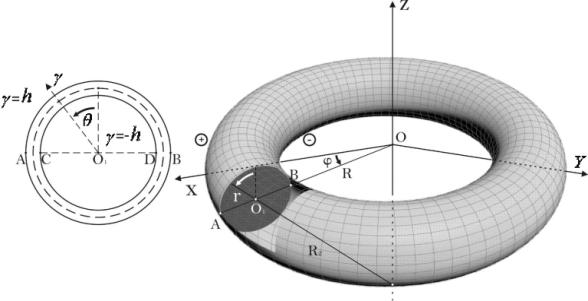
                                                              Фиг.

 

Материал оболочки термически анизотропный (6 коэффициентов тепловой анизотропии) и неоднородный по продольным координатам .

         На внешней и внутренней поверхностях оболочки пусть заданы их температуры (условия первой краевой задачи теплопроводности [5])

                                         (1.1)                                          

или нормальные компоненты плотности вектора потока теплоты

                                             (1.2)                                           Требуется найти температурную функцию и исследовать тепловое поле оболочки

Перепишем уравнения  теплопроводности термически анизотропного тела в криволинейных триортогональных координатах [2,6–8]

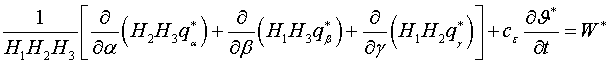
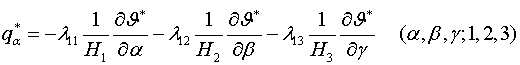                                   (1.3)             

               

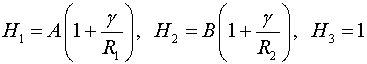
      Здесь – коэффициенты Ламе,  – коэффициенты первой квадратичной формы координатной поверхности, главные радиусы кривизны координатной поверхности, – удельная теплоемкость при постоянной деформации, – коэффициенты теплопроводности, – удельная плотность источника тепла,  компоненты плотности вектора потока теплоты.

  Для рассматриваемой тороидальной оболочки: , а также

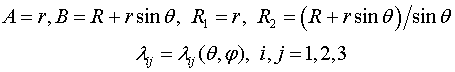                      (1.4)   

         Для решения поставленных краевых задач представим все  заданные в (1.1)–(1.3)   функции в виде

                                                                     (1.5)                                                          

Одновременно искомые функции  представим в виде         (1.6) 

 (условия (1.5),(1.6) вносят некоторые ограничения, которые будут сняты позже).  

Подставив (1.5), (1.6) в (1.1)–(1.4) затем преходим к безразмерным координатам по формулам

                                          (1.7)

и получаем

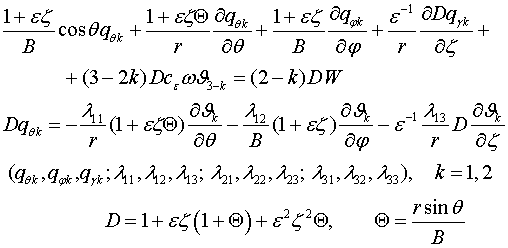         (1.8) 

Уравнения (1.8) сингулярно возмущены геометрическим малым параметром .

 Их  асимптотическое решение складывается из двух решений: внутреннего  (основного) решения, доминирующего внутри области занимаемой тонким телом и решения задачи для пограничного слоя , которое экспоненциально убывает (затухает) по направлению внутренней нормали к поверхности торцов [9–12]. Поверхность рассматриваемой тороидальной оболочки считается непрерывной и замкнутой, поэтому здесь строится только внутреннее решение, которое ищется в виде асимптотического разложения [9,10]

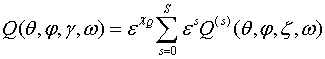                       (1.9)                                        где  – для температурной функции и  – для плотности

потока теплоты.

Одновременно заданную функцию интенсивности источника тепла представим в виде асимптотического разложения

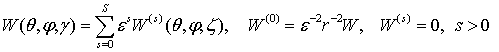                  (1.10)          

Представление (1.10) определяет такой асимптотический порядок источника тепла, который обеспечивает его интенсивное влияние на тепловой режим оболочки начиная с первого шага итерационного процесса.

Подставив (1.9), (1.10) в преобразованную систему (1.8) и приравняв в левых и правых частях уравнений коэффициенты при получаем непротиворечивую систему рекуррентных разрешающих уравнений, которая имеет вид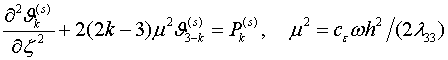            

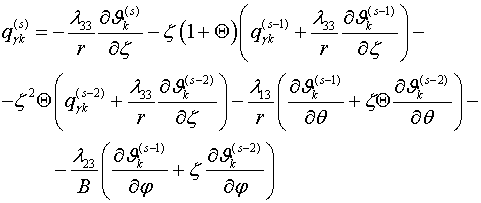                     (1.11)

  Здесь обозначены     

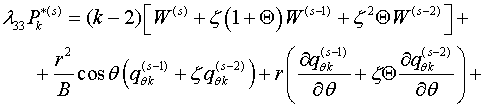
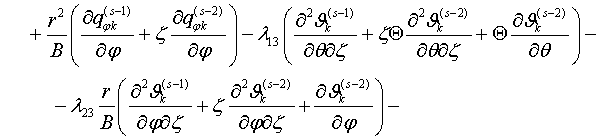    (1.12)                                                                                                        

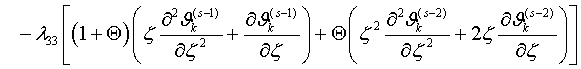
2. Решения краевых задач. Система уравнений (1.10) содержит параметр зависящий  от частот  изменения во времени внешних воздействий. В зависимости асимптотического порядка   изменится асимптотика системы разрешающих уравнений. Рассмотрим два случая:

   а. Если    величина порядка , общее решение системы (1.11) имеет вид 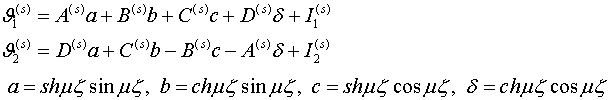(2.1)

где – частное решение системы неоднородных уравнений, которoе определяeтся формулами

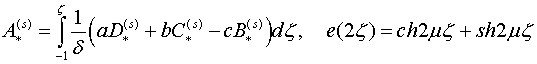
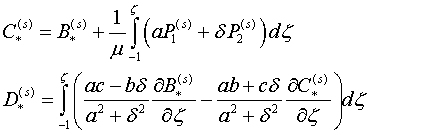                                    (2.2)                                       

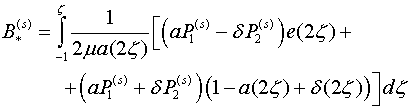
   Общий интеграл системы (2.1) содержит четыре функции интегрирования  ,  которые однозначно  определяются из граничных условий.

         Когда на поверхностях тороидальной оболочки заданы значения температурной функции (граничные условия (1.1)),  функции интегрирования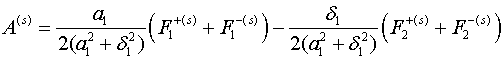       

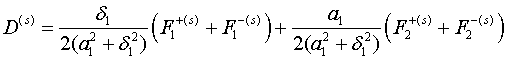
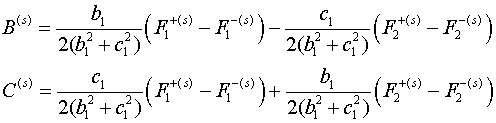             (2.3)         

           

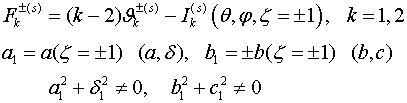
Когда же заданы проекции вектора интенсивности потока теплоты на нормали к поверхностям тороидальной оболочки (граничные условия (1.2)),  функции интегрирования  получают вид

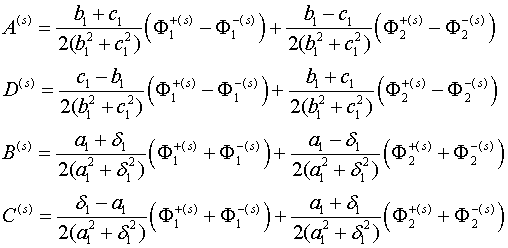           (2.4)

Здесь обозначены

                  

      

 

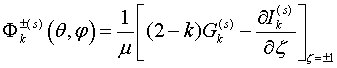
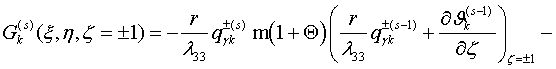
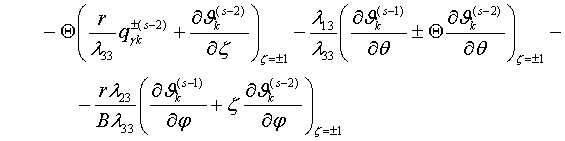      (2.5)

Заметим, что в рассмотренных краевых задачах амплитуды тепловых волн (2.4) не содержат особенности. Это свидетельствует о том, что тепловые волны не подвергаются резонансу.

б. Пусть частота теплового возмущения  малая величина, при которой  имеет асимптотический порядок . Тогда система (1.11) принимает вид

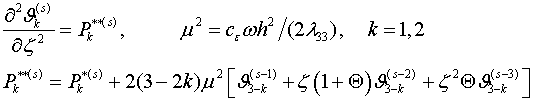               (2.6) 

что соответствует состоянию квазистационарной задачи теплопроводности.  Ее общее решение имеет вид 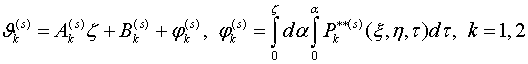                                (2.7)

Удовлетворив граничным условиям (1.1) получаем

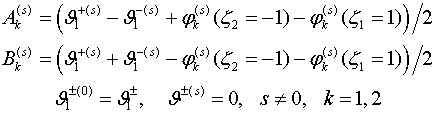                       (2.8)                                    

Заметим, что с точностью первого шага итерации тепловое поле по толщине оболочки меняется линейно, следовательно плотность теплового потока постоянна  с указанной точностью.

в.  Асимптотическое решение краевой задачи стационарной  теплопроводности тороидальной оболочки получится из решения (2.6)–(2.8)  квазистационарной задачи, принимая   и , при учете (1.12).

Выведенные  решения поставленных краевых задач теплопроводности для тороидальных оболочек в виде рекуррентных формул позволяют вычислить температурную функцию и компоненты интенсивности вектора потока теплоты с любой асимптотической точностью , если изменяемости [2]  заданных функций имеют порядок .  Заметим, что порядок применения выведенных рекуррентных формул является готовым алгоритмом компьюторной программы для аналитического (при необходимости) и численного решения поставленных краевых задач.

3. Примеры задач квазистационарной и стационарной теплопроводности. Для иллюстрации применения выведенных рекуррентных формул, рассмотрим конкретные примеры:

a. На внешней и внутренней поверхностях термически однородной и ортотропной тороидальной оболочки заданы температуры условиями (1.1),(1.5), где  малая величина, при которой  имеет асимптотический порядок . Требуется определить температурную функцию оболочки, если отсутствует источник тепла: .

Ограничиваясь первыми тремя шагами итерации, с асимптотической точностью , по рекуррентным формулам решения квазистационарной задачи теплопроводности (2.6)–(2.8) при учете (1.12),  для температурной функции тороидальной оболочки получаем

                                                              

    

 

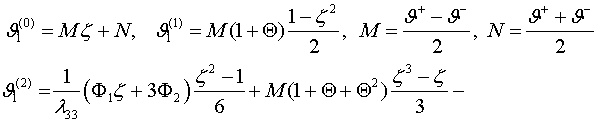
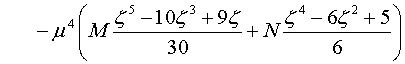                                      (3.1)

                                                 

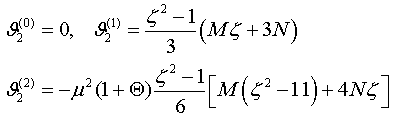
Здесь обозначены

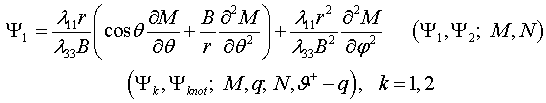         (3.2)

б.  Ha внешней поверхности термически однородной ортотропной тороидальной оболочки заданы неклассические условия:  постоянные во времени температура и  плотность вектора потока теплоты

                  (3.3)

а на внутренней поверхности условия не заданы и отсутствует источник тепла: . Требуется определить температурную функцию тороидальной  оболочки в рамках задачи нестационарной теплопроводности.                         

Taкие задачи иногда называют ,,некорректными по Адамару” [13,14]. В работе [15] доказно  существование решения уравнения Лапласа, которое  на границе полуплоскости одновременно удолетворяет условиям и задачи  Дирихле, и задачи Неймана. Это утверждение обобщено для полупространства [16]. Поскольку дним из методов решения упомянутых  выше “некорректных” задач считается приближенный метод [14]  , учитывая большое прикладное значение таких задач и эффективность асимптотического  метода  для решения краевых задач,  для полосы и пластины решены неклассические задачи соответственно теорий стационарной теплопроводности и упругости [17,18]. Выведенные рекуррентные формулы асимптотического решения краевой задачи стационарной  теплопроводности тороидальной оболочки (2.6)–(2.8) при  и , ,  позволяют решить сформулированную неклассическую задачу. Приводим это решение с точностью первых трех шагов итерации

                      

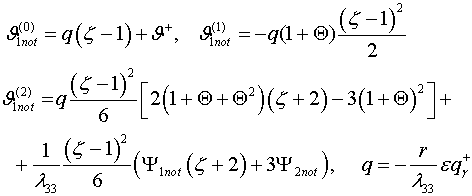             (3.4)

Для установления связи между решениями классической краевой задачи стационарной теплопроводности  (3.1) при условий   и  и неклассической задачи (3.4) определим из последнего (предполагаемую) температуру   на внутренней поверхности тороидальной оболочки (шланга) принимая  в формулах (3.4). Она равна

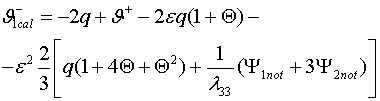                              (3.5)

Подставив  вычисленное значение температуры внутренней поверхности   в решение классической задачи стационарной теплопроводности  при учете (3.4), с точностью первых трех шагов итерации [19] заметим, что они совпадают с точностью  , те.

                                                                                                   (3.6)

Таким образом выведенные рекуррентные формулы позволяют с  любой асимптотической точностью  решить кревые задачи стационарной теплопроводности для тороидальных оболочек как с классическими, так же  с неклассическими граничными условиями , которые совпадают с такой же точностью, при соответствующем подборе функций заданных на поверхностях  оболочки.

 Заметим, что когда R→∞,  тороидальная оболочка превращается в радиуса  цилиндрическую оболочку бесконечной длины. Все сформулированные задачи и их решения остаются в силе для цилиндрической оболочки бесконечной длины при предельном переходе R→∞. При этом следует учесть, что тепловое поле не меняется по длине цилиндра.

Приведенные выше решения получены при функциях (2.1), входящих в граничные условия (1.1),(1.2) и соотношения (1.5),(1.6). Можно рассмотреть более общий случай зависомости от времени, заменив все заданные в (1.1), (1.2), (1.5) функции их образами  преобразования Фурье

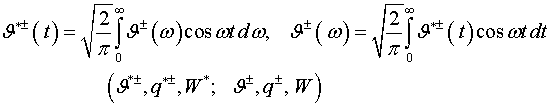      (3. 7)

а неизвестные величины: температурную функцию и  компоненты плотности вектора потока теплоты искать в виде

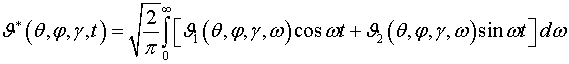        (3.8)

и в аналогичном виде искать соответствующую производную по времени

Такие представления оставляют в силе все выведенные формулы для образов искомых величин. После решения краевых задач возникнет необходимость возвратиться к оригиналам искомых величин, применив обратное преобразование Фурье.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                          Литература

   1. Булгаков В.Н. Статика тороидальых оболочек. Киев:  Изд-во АН УССР,

      1962. 100с.

 2. Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука,1976. 512с.

3. Асратян М.Г., Геворкян Р.С. Cмешанные краевые задачи термоупругости  для анизотропных в плане неоднородных тороидальных оболочек // ПММ АН РФ. 2010.Том. 74. Вып. 3. С.433-440.

4. Àãàëîâÿí Ë.À. Ãåâîðêÿí Ð.Ñ.  Динамические задачи термоупругости для анизотропных неоднородных тороидальных оболочек//В кн.: Проблемы динамики взаимодействия  деформируемых сред.  Ереван: Инс.механики НАН РА, 2008. С.27-35.

 5. Лыков А.В. Теория теплопроводности. М.: ГИТТЛ, 1952. 392с.

6. Nowacki W. Dynamiczne Zagadnienia Termosprezystosci. Warszawa: PWN, 

    1966.= Новацкий В. Динамические задачи термоупругости. М.: Mир, 1970.256с.

7. Коваленко А.Д. Основы термоупругости. Киев: Наук. думка,1970.239 с.

8.  Немировский Ю.П., Янковский А.П. Метод асимптотических разложений решений  задачи стационарной теплопроводности слоистых анизотропных неоднородных  пластин. // ПММ. 2008. Т. 72, Вып. 1. С. 157-175.

9. Агаловян Л. А. Асимптотическая теория анизотропных пластин и

       оболочек. М: Наука-физмат, 1997. 414с.

10. Агаловян Л. А., Геворкян Р. С. Неклассические краевые задачи анизотропных слоистых балок, пластин и оболочек Ереван: Гитутюн, 2005. 468с.

11. Агаловян Л. А.  Упругий пограничный слой для одного класса плоских задач // Меж вуз. сборник н. трудов. Механика. Ереван: Изд-во ЕГУ, 1984. C. 51-58.

12. Геворкян Р. С. Асимптотика пограничного слоя для одного класса краевых задач анизотропных пластин // Изв АН Арм. ССР. Механика. 1984 Т. 37. . №  6. С. 3-15.

13. Лаврентьев М.М., Романов В.Г., Шишатский С.П. Некоторые задачи математической физики и анализа. М.: Наука, 1980. 286 с.

14. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 285с.

 15.  Келдыш М.В. О приближении голоморфных функций целыми функциями// ДАН СССР, 1945. Т.47,  №  4. С. 243-145

16.  Аракелян Н.У. О задачах  Дирихле и Неймана для гармонических функций// Изв.НАН Армении. Математика. 2008. Т.43. № 6. С.21-38.

17. Геворкян Р.С.Об асимптотическом анализе решений  корректных и “некорректных по Адамару” задач  для эллиптических уравнений (теплопроводности) математической физики// В кн. Сб. н. трудов  международной конференции “Актуальные проблемы механики сплошной среды” 4-8 окт. Ереван, 2010. С. 182–166.

18. Lenser A. Aghalovyan, Ruben S. Gevorgyan, Avetik V.Sahakyan. Mathematical Simulation of Collision of Arabian and Euroasian Plates on the Base of GPS Data // Изв.НАН Армении. Механика. 2005. Т.58. №4. С.3-9.

19. Ломов С.А. Введение в общую теорию сингулярных возмущений. М.: Наука, 1981. 398 с.

         Армения.

 

             

 

                                       Сведения об авторах

Рубен Степанович Геворкян − профессор, доктор

физ-мат. наук, ведущий научный сотрудник

института Механики НАН РА.

Тел.:       (37410) 270828,   (37493) 536883

e-mail:   gevorgyanrs@mail.ru

Дом. адрес:            ул. Киевяна 12, кв. 6.

                    0028, Ереван, Армения.

 

 

Aрмине Гамлетовна Саркисян

кандидат физ-мат. наук, старший научный сотрудник

института Механики НАН РА.

Тел.:   (37410) 610423,   (37477) 459033                 

e-mail:  armin.sa@bk.ru

Дом. адрес:         Аван, ул. Дуряна 32, кв. 51.

                   0044, Ереван, Армения.