УТОЧНЕНИЕ ИЗМЕРЯЕМЫХ ДАННЫХ ПО ПРЕДВАРИТЕЛЬНОЙ ИНФОРМАЦИИ О СВЯЗЯХ МЕЖДУ НИМИ

В.В. Митюков

Ульяновское высшее авиационное училище гражданской авиации (институт), Ульяновск, Россия, v.mityukov@gmail.com

Измеряемая информация в различных исследовательских задачах представляется в виде числовых массивов данных, записанных с некоторым шагом дискретизации. Наличие математической модели для исследуемой задачи означает, что между измеряемыми переменными (числовыми рядами) существует априорная избыточность в виде имеющихся между ними связей (уравнений). Эта избыточность может быть использована для уточнения и корректировки измеренных данных, как указывается в работе [1].

В геометрической интерпретации значения измерений должны находиться в некотором подмножестве пространства измеряемых переменных, которое определяется связями между ними. Например, наличие одной связи определяет в трехмерном пространстве такое двумерное подмножество как поверхность, а двум связям удовлетворяет одномерная линия пересечения двух поверхностей. Только этому одномерному подмножеству (линии) должны принадлежать значения трех рядов данных, при наличии двух связей между ними.

Сами связи между переменными чаще всего бывают представлены в виде алгебраических и/или дифференциальных уравнений. Последний вид уравнений требуется напомнить подробнее. Геометрически, общим решением обыкновенного дифференциального уравнения (ОДУ) первого порядка является семейство функций одной переменной. Из этого семейства можно выделить одну из функций y(t) (частное решение), которое определяется как исходящее из некоторой начальной точки {t₀, y₀} (задача Коши), или как удовлетворяющее значениям y_i при различных значениях t_i , чаще концевых (краевая задача). Возможны и другие разновидности связей, например, в виде интегральных и интегро–дифференциальных уравнений.

В частности, модель движения некоторого транспортного средства в рамках модели твердого тела [2], сводится к системе ОДУ первого порядка. В системе координат (СК), фиксированной относительно твердого тела, уравнение движения центра масс под действием суммарного вектора внешних сил F и уравнение вращения вокруг центра масс под воздействием суммарного момента M, для системы из k материальных точек с массами m_k и скоростями V_k на расстояниях Dr_k от центра масс примут следующий вид:

где – вектор количества движения системы точек (тела)

– вектор момента количества движения тела

w – вектор скорости вращения системы точек (твердого тела)

Векторы p и L желательно определить как усредненные для всей совокупности точек объекта. Можно показать, что исходя из понятия центра масс, определяемого как и используя фиксированное положение связанной СК, эти векторы приводятся к интегральному для всей недеформируемой системы точек виду [3]:

( 1 )

где m – общая масса системы материальных точек

V – вектор абсолютной скорости центра масс

I – тензор инерции

Для однозначного определения положения твердого тела, систему динамических уравнений необходимо замкнуть кинематическими уравнениями, связывающими векторы движения V и w этого тела (или связанной с телом СК) с векторами поступательного r и углового j его положения относительно СК, выбранной за инерциальную:

( 2 )

В проекциях на трехмерную СК, 4 полученных векторных уравнения (1), (2) приводятся к системе ОДУ 1-го порядка, состоящей из 12 уравнений. Можно сказать, что 12 дифференциальных связей, наложенных на 13-мерное пространство (12 проекций векторов V, w, r, j и независимая переменная t), определяют в нем одномерное подмножество в виде некоторой линии. При наличии измерений всех 12-ти переменных (12 числовых рядов), алгоритм их согласования с 12-ю уравнениями, то есть принадлежности к задаваемой ими одномерной линии, определялся бы следующим естественным образом:

Систему ОДУ 1-го порядка, приведенную к нормализованному виду , можно записать в интегральном представлении:

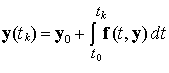( 3 )

где y( t_k ) – значения 12-мерной вектор–функции y(t) в точках t_k

Измеренные значения вектора y_k должны совпадать с y(t_k), полученными путем численного интегрирования выражения (3) (например, воспользовавшись алгоритмом [4]). В общем случае следует проводить интегрирование (3) порциями по m точек от t_k до t_k+m. (k = 0, 1…n).

Задача уточнения корректируемых значений y_k, является прежде всего задачей оптимизации. В качестве критериев близости исправляемых значений вектора y_k к точному решению системы ОДУ – y(t_k), могут служить следующие два, наиболее распространенные в вычислительной практике:

· метод коллокаций, состоящий в точном выполнении равенcтва нулю длины вектора невязки в точках t _k (k = 0, 1, .. n).

· метод наименьших квадратов, вытекающий из условия минимума суммы квадратов всех невязок на заданной системе точек t _k (суммы скалярных произведений векторов невязки):

На практике все гораздо сложнее. В представлениях сил и моментов (их сложность и полнота), включающих в себя как минимум силы и моменты от двигателя и аэродинамического воздействия, изначально заложена неопределенность из-за сложности и громоздкости описания действующих на объект сил и моментов. Построение достаточно полной и адекватной модели сил и моментов – чрезвычайно трудная задача. Из всех полученных векторных уравнений, безупречно точными являются только кинематические (2).

Предлагаемый подход к повышению точности измерямых координат и параметров движения некоторого объекта может найти применение в следующих задачах:

· В задачах инерциальной навигации для уточнения вычисляемых параметров движения объекта в режиме реального времени.

· При расследованиях летных происшествий для восстановления и уточнения записанных параметров движения объекта и предполагаемой траектории.

1. Касьянов В.А. Моделирование полета: Монография. –К.: НАУ, 2004.– 400 с.

2. Халфман Р. Динамика: Пер.с англ. –М.: Наука. Гл. ред. физ.-мат. литер., 1972. – 568 с.

3. Митюков В.В. Согласование измеряемых параметров полета с априорно заданными связями между ними. Матерiали X мiжнародноï науково-технiчноï конференцiï «АВIA–2011». –Т.1. –К.: НАУ, 2011. – с. 6.38–6.41

4. Митюков В.В. Унифицированный алгоритм дифференцирования и интегрирования дискретных числовых массивов. «Современные информационные технологии и ИТ-образование». Сборник докладов V международ научно-практической конференции: учебно-метод. пособие. Под ред. проф. В.А. Сухомлина. – М.: ИНТУИТ.РУ, 2010. – с. 509–513.