Божанов Е.Т., Ибраимкулов А.М.,

Касымбекова М.Т., Койшыбаева Ж.Ж.

Казaхский национальный технический университет имени К.И.Сатпаева

ВЫПУЧИВАНИЕ СИМУЛЯЦИОННОЙ МОДЕЛИ РЕЗЕРВУАРА В ЗАВИСИМОСТИ ОТ ВИДА КРИТИЧЕСКОЙ СИЛЫ ПО ФОРМЕ КРИТИЧЕСКОЙ ДЕФОРМАЦИИ ТРАПЕЦИЕВИДНОЙ ФОРМЫ И ГИПЕРБОЛИЧЕСКИЕ ТОНКОСТЕННЫЕ ГРАДИРНИ

Постановка задачи

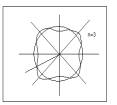
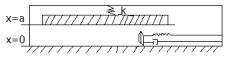
Пусть поперечное сечение симуляционной модели резервуара представляет собой гиперболические тонкостенные градирни, а критическая деформация поперечного сечения трапециевидной формы. (Рис. 1).

Рисунок №1

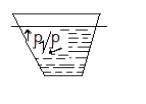
Рисунок №1а

Рисунок №1с P-гидростатическое давления, - вертикальные составляющие силы на наклонные стенки

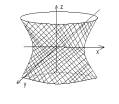
Рисунок №1d градирни

Гидростатическое давление нефти на глинистые стенки резервуара как на цилиндрический сосуд типа парадокса Паскаля.

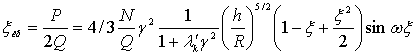(1)

где

Давление на внутренные глинистые стенки примем

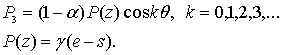(2)

Здесь γ- плотность жидкости, – высота резервуара, - длина дуги медианы.

Если �� есть координата, определяющая параллельные круги, то

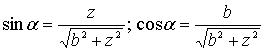(3)

параметры гиперболы, толщина поперечного сечения.

Нагрузку упруго – вязкой среды со стороны нефтяной смеси возьмем в виде модели Фоихта при предположении

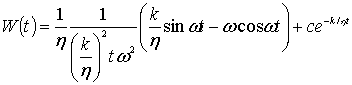
, (4)

Распределение плотности жидкости в поперечном сечении

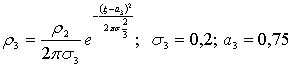(5)

Здесь

Здесь среднее квадратическое отклонение.

Уравнение движение резервуара произвольного сечения представим в виде модели Б – 1 с использованием технологических характеристик нефтяного пласта сучетом внутренного трения в промежуточных процессах (Рис.2).

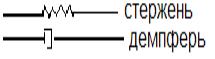
(6)

огда уравнение выпучивания резервуара по формам критической деформации трапециевидной формы имеет вид [1],[2]

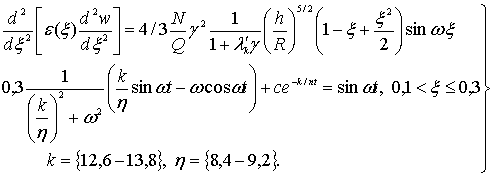(7)

Граничные условия:

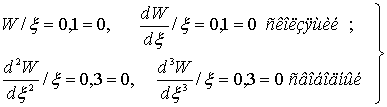(8)

Решение

Из граничных условии (8) и первого дифференциального уравнения системы (7) в предположении:

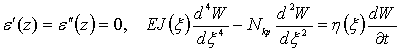(9)

Получим

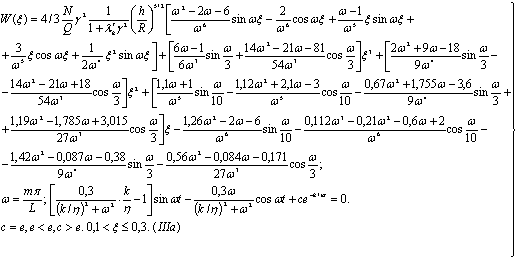(10)

Таким образом, распределение поверхностей уровня поле велины критических давлении следующие:

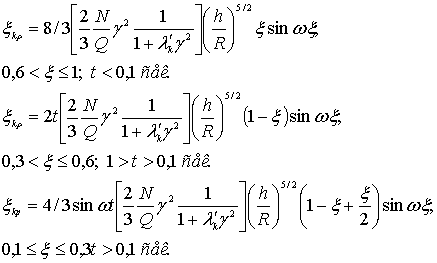
В частности, если систему (7) возьмем в виде

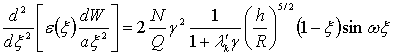(11)

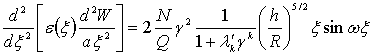(12)

при тех же граничных условиях (8), то получим соответствующие алгебраические уравнения выпучивания симуляционной модели резервуара в зависимости от вида формы критической деформации типа гиперболической тонкостенной градирни. Разрешающие уравнения вдоль параллели относительно функции напряжения будет:

(13)

где

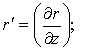
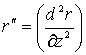
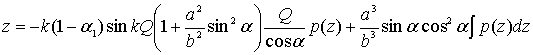(15)

Здесь:

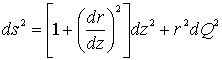, (15)

;

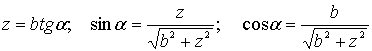(16)

Здесь координата, определяющая параллельный круг, на котором отыскиваются компоненты внутренних усилии градирни, и – малые и большие оси однополостного гиперболоида вращения

(17)

В формулах (10) анизотропные характеристики – , ; число волн в поперечном сечении - , нелинейные деформационные процессы согласно теории М.А.Био, А.Н.Гузя, В.В.Новожилова, и А.С.Лейбснзона.

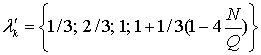(18)

резервуара с толщиной - , длиной - , внутренным радиусом – .

Таким образом, построение графиков функции по формуле (4), по формуле (5); по формуле (10) при следующих данных:

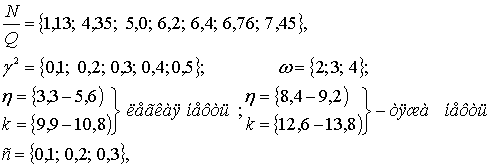
дает полную картинку для анализа выпучивания симуляционной модели резервуара в зависимости от вида формы критической деформации гиперболические тонкостенные градирни поперечного сечения.

ЛИТЕРАТУРА

[1]. Божанов Е.Т., Ибраимкулов А.М., Жаканова А., Дмитриева Н., “Исследование проблем устойчивости и выпучивания композитов из чередующих двух “бутербродов” под действием критической силы по теориям М.А.Био, В.В.Новожилова, А.Н.Гузя, Л.С.Лейбснзона и А.Ю.Ишлинского”, труды международной научно-практической конференции “Информационные и телекоммуникационные технологии”, том II, Алматы, 2012г.

[2]. Божанов Е.Т., Ибраимкулов А.М., Скакова А.Б. “Об одной математической модели технологии разработки нефтяных месторождении из N-го горизонта из 4-х чередующих приведенных слоев”, труды II-ой международной научной конференции “Высокие технологии - залог устойчивого развития”, том II, Алматы, 2013г.