Божанов Е.Т., Акимжанова Ш.А., Байбатыр К. - КазНТУ,

Кожахметов О.С. АИЭС

Казaхский национальный технический университет имени К.И.Сатпаева

Движение нефтегазовой смеси по стволам траектории скважины под действием критической силы N_кр, когда форма поперечного сечения конусоидального типа.

Постановка задачи.

Пусть математико-гидродинамическое моделирование резервуара, лежащего на основании типа Винклера под действием критической силы N_кр приводит к дифференциальному уравнению изогнутой оси поперечного сечения резервуара [1]-[4] к виду:

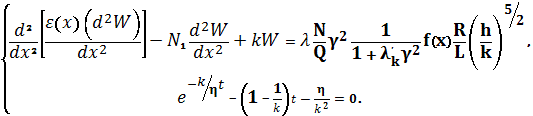(1)

Нагрузку упруго-вязкой среды со стороны нефтяной смеси и изменение плотности поперечного сечения резервуара на отрезке 0≤х≤L представим в виде модели Фоихта [5]

, , (2)

где а=0.35; σ=0.3; ρ₁=ρ(0,σ)=const при предложениях

=0, 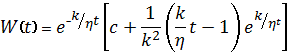при p(t)=t (3)

Тогда первое уравнение системы (1) имеет вид:

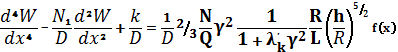. (4)

Общее решение (4) есть (5)

Где -есть общее решение однородной части, а -какое-нибудь частное решение дифференциального уравнения (4). Характеристическое уравнение однородной части дифференциального уравнения (1) перепишем в виде

или (6)

Возможны случаи:

А)-случай:

B)-случай:

C)-случай:

1.1 Рассмотрим первое уравнение системы (1) в случае А).

(7)

При граничных условиях:

(8)

Решение

Корни характеристического уравнения:

, ,

Следовательно, общее решение:

(9)

На основании граничных условий (8), решая аналогичны образом задачи (7) получим:

(10)

Здесь

; , ; ; ; ; (11)

1.2 Рассмотрим первое уравнение системы в случае В).

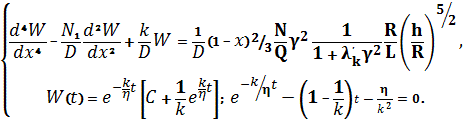(12)

При граничных условиях:

(13)

Решение

Корни характеристического уравнения действительные, различные:

, ,

; ; ; (14)

Следовательно, общее решение:

(15)

На основании (13) из (15) получим:

. (16)

Здесь

, ; ; ; ;; (17)

1.3 Рассмотрим первое уравнение системы в случае C).

(18)

При граничных условиях:

(19)

Решение

Корни характеристического уравнения комплексные:

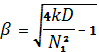; ; ; ; ; ; ; ; ; ; . (20)

Следовательно, общее решение (18):

(21)

На основании (19) из (21) получим:

. (22)

Здесь

,; ; ; ; ; (23)

Выводы: Движение в нефтегазовой смеси по стволам траектории скважины, которая расположена в симуляционной модели резервуара, должно быть плавноизменяющееся, однако в местах резкого изменения формы и толщины резервуара невозможно избежать разницы деформации в местах стыка или сопряжения. Создание геолого-технологических моделей для расчетов с использованием вязко-упругого сопротивления, геостатическое моделирование представляют инженерам возможности более эффективно прогнозировать и визуализировать движение нефтегазовой смесипо стволам траектории скважины под действием критической силы N_кр, когда форма поперечного сечения конусоидального типа.

Литература:

1. Божанов Е.Т., Ержанов Ж.С. «Исследование проблем устойчивости гибких тел, пластин и оболочек и их приложения», Алматы, 2001г, 324с.

2. Рахимбекова З.М. «Нелинейные стержневые системы за пределом упругости», Алматы, 2002г.

3. Божанов Е.Т., Ибраимкулов А.М., Жаканова А., Дмитриева Н. «Исследование проблем устойчивости и выпучивания композитов из чередующих двух «бутербродов» под действием критической силы по теориям М.А. Био, В.В. Новожилова, А.Н. Гузя» //Труды межд. науч.-прак. конф. «Информационные и телекоммуникационные технологии: образование, наука, практика». Том II.- Алматы, 2012.

4. Божанов Е.Т., Ибраимкулов А.М., Дмитриева Н., Жаканова А. «Выпучивание композитов в зависимости от предельной гибкости поперечного сечения по теориям Л.С. Лейбензона, А.Ю. Ишлинского» //Труды межд. науч.-прак. конф. «Информационные и телекоммуникационные технологии: образование, наука, практика». Том II.- Алматы, 2012.

5. Spears & Associates: “Drilling and Production Outlook”, March 1996.