About the similarity of particle and photon tunneling
and multiple internal reflections in 1-dimensional, 2-dimensional and
3-dimensional photon tunneling.
V.S.Olkhovsky
Institute for Nuclear Research
of NASU, Kiev-028, prospect Nauki, 47,Ukraine; olkhovsky@mail.ru
Abstract: The formal mathematical
analogy between time-dependent quantum equation for the non-relativistic
particles and time-dependent equation for propagation of electromagnetic waves had
been studied in [1,2]. Here we deal with the time-dependent Schrödinger
equation for non-relativistic particles and with time-dependent Helmholtz
equation for electromagnetic waves. Then, using this similarity, the tunneling
and multiple internal reflections in 1D (1-dimensional), 2-D and 3-D particle
and photon tunneling will be studied. Finally some conclusions and future
perspectives for further investigations are presented.
PACS 03.65.Xp; 42.50.Xa
Key
words photon tunneling, similarity of photon and particle tunneling, Hartmann
phenomemnon, superluminality
I. Introduction.
Here we consider the formal mathematical analogy between time-dependent
Schroedinger equation for non-relativistic particles and with time-dependent
Helmholtz equation for electromagnetic waves and also such similarity of probabilistic
interpretation between particle wave function and classic electromagnetic wave
packet (being the “wave function of a single photon”, as follows from [1,2]),
which is sufficient for the same definition of mean times and durations for
processes of propagation, collisions and tunneling of both particles and
photons. The only difference in such analogy is caused by linear dependence of
energy and impulse for photons and the quadratic dependence of energy from
impulse for non-relativistic particles having rest mass. And it induces the
physical difference in the spreading of particle wave packets in comparison
with photons.
II.
Photon tunneling. Concretely let
consider hollow narrowed rectangular wave-guide, depicted in Fig.1 (with cross
section a ´ b in narrowed
part, a < b), which was
used for experiments with microwaves [3].
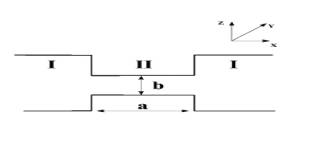
Fig.1. When radio-waves in the microwave range are propagating along the
wave-guide, narrowed segment (with cross width which is less than wavelength
cutoff) appears as photonic barrier.
Inside it, time-dependent wave equation
for any vector ![]() ,
, ![]() ,
, ![]() (
(![]() is a vector potential with the additional calibration
condition div
is a vector potential with the additional calibration
condition div ![]() = 0,
= 0, ![]() = –(1/c)
= –(1/c) ![]()
![]() /
/![]() t is an electric field strength,
t is an electric field strength, ![]() = rot
= rot ![]() is a magnetic field strength)
has the form
is a magnetic field strength)
has the form
![]()
![]() – (1/c2 )
– (1/c2 ) ![]() 2
2![]() /
/![]() t 2 = 0. (1)
t 2 = 0. (1)
It is known (see, for
instance, [4-6]), that for the boundary conditions
Ey = 0 for z = 0 and
z = a , (2)
Ez = 0 for y = 0 and y = b
,
The monochromatic
solution (1) can be
represented as a superposition of following waves:
Ex = 0 ,
Ey± = Eo sin(kz z) cos(ky y) exp[i(![]() t ±
t ± ![]() x)] , (3)
x)] , (3)
Ez± = –Eo (ky /kz ) cos (kz z) sin(ky y) exp[i(![]() t ±
t ± ![]() x)]
x)]
(here we have
chosen TE-waves) with kz2+ky2+![]() 2=
2=![]() 2 /c2=(2
2 /c2=(2![]() /
/![]() )2,
kz = mp /a , ky
=n
)2,
kz = mp /a , ky
=n![]() /b , m and n are integer numbers. Òhus,
/b , m and n are integer numbers. Òhus,
g= 2![]() [(1/
[(1/![]() )2 - (1/
)2 - (1/![]() c)2]1/2,
(1/
c)2]1/2,
(1/![]() c)2 = (m/2a)2
+ (n/2b)2 , (4)
c)2 = (m/2a)2
+ (n/2b)2 , (4)
where ![]() is real (
is real (![]() = Re
= Re![]() ), if
), if ![]() <
<![]() c and
c and ![]() is imaginary (
is imaginary (![]() = i
= i![]() em ), if
em ), if ![]() >
>![]() c. Similar expressions can be obtained
for TH-waves [1,5].
c. Similar expressions can be obtained
for TH-waves [1,5].
Generally speaking, the solution of
equation (1) can be written in the form
of wave packet, constructed from monochromatic solutions (3), like the solution of
time-dependent Schroedinger equation for non-relativistic particles in the form
of wave packet, constructed from the monochromatic waves. Moreover, in
representation of the primary quantization, the probabilistic one-photon wave
function usually is described by a wave packet for ![]() [1,2], for instance,
[1,2], for instance,
![]() (
(![]() ,t) =
,t) =
![]() (
(![]() ) exp (i
) exp (i![]()
![]() - iko t)
(5)
- iko t)
(5)
in the case of
plane waves, where ![]() ={x, y, z},
={x, y, z}, ![]() (
(![]() )=
)=![]() ki (
ki (![]() )
)![]() i (
i (![]() ),
), ![]() i
i![]() j =
j =![]() i j ,
i j , ![]() i (
i (![]() )
)![]() =0, i,j=1,2 (or
y,z, if
=0, i,j=1,2 (or
y,z, if ![]()
![]() =kxx), ko=
=kxx), ko=![]() /c=e/
/c=e/![]() c, k=|
c, k=|![]() |=ko , ki (
|=ko , ki (![]() ) is an
amplitude of the probability of possessing by photon the impulse
) is an
amplitude of the probability of possessing by photon the impulse ![]() and polarization i and then the quantity |ki(
and polarization i and then the quantity |ki(![]() )|2d
)|2d![]() is proportional to the probability that photon has the
impulse in the interval
is proportional to the probability that photon has the
impulse in the interval ![]() and
and ![]() +d
+d![]() in the polarization state
in the polarization state ![]() i. Although it is impossible to
localize the photon in the direction of its polarization, nevertheless in a
certain sense for one-dimensional motion it is possible to use the space-time
probabilistic interpretation (5) along axis x (the direction of motion) [2]. Usually one
uses not the probability density and probability flux density on the base of
the correspondent continuity equation directly,
but the energy density so and the flux of energy density sx (although
they represent the components of non 4-vector, but of tensor of energy-impulse)
on the base of the correspondent continuity equation [7], which we write in
two-dimensional (spatially one-dimensional)
lorentz-invariant form:
i. Although it is impossible to
localize the photon in the direction of its polarization, nevertheless in a
certain sense for one-dimensional motion it is possible to use the space-time
probabilistic interpretation (5) along axis x (the direction of motion) [2]. Usually one
uses not the probability density and probability flux density on the base of
the correspondent continuity equation directly,
but the energy density so and the flux of energy density sx (although
they represent the components of non 4-vector, but of tensor of energy-impulse)
on the base of the correspondent continuity equation [7], which we write in
two-dimensional (spatially one-dimensional)
lorentz-invariant form:
¶ so /![]() t +
t +![]() sx /
sx /![]() x = 0 ,
(6)
x = 0 ,
(6)
where
so
=(![]() *
*![]() +
+ ![]() *
*![]() )/ 8
)/ 8![]() , sx = c Re [
, sx = c Re [![]() *
*![]() ]x /2
]x /2![]() (7)
(7)
and axis x is directed along the motion axis (mean impulse) of wave packet (5).Then, as the normalization condition we choose the equality of spatial integrals so and sx for mean photon energy and mean photon impulse respectively or simply unit flux density for energy sx. Bypassing the problem of impossibility for the direct spatial probabilistic interpretation (5), we can define conditionally probability density
![]() dx = So dx /
dx = So dx / ![]() So dx
, So =
So dx
, So = ![]() so dydz (8)
so dydz (8)
to find (localize)
photon in the spatial interval (x,x+dx)
along axis x at time t, and probability flux density of
Jem,x dt=Sx dt /![]() Sx dt, Sx =
Sx dt, Sx =![]() sx dydz (9)
sx dydz (9)
photon passage through point (plane) x in the time interval (t,t+dt), quite similarly to the probabilistic proprieties for non-relativistic particles. Justification and conditionality of such definitions is supported also by coincidence of the group velocity for wave packet and the velocity of the energy transport which is accepted for electromagnetic waves (at least for plane waves) in [9]. Hence, in a certain sense, in time analysis along the motion direction (1) the wave packet (5) is totally similar to the wave packet for non-relativistic particles and (2) similarly to standard quantum mechanics one can define the mean time of photon (electromagnetic
wave packet)
passage
through point x [8]:
<t(x)> = ![]() t Jem,x dt =
t Jem,x dt = ![]() t Sx(x,t)dt/
t Sx(x,t)dt/![]() Sx (x,t)dt ,
(10)
Sx (x,t)dt ,
(10)
where for natural
boundary conditions ki (0)=ki (¥)=0 in energy
representation (e=![]() cko) one can use the same form of time
operator, as for particles in non-relativistic quantum mechanics – and
therefore to show the equivalence of calculations for <t(x)>, variance Dt(x) etc in both time and energy
representations. Òhen for wave
packets like in Fig.1 for the boundary conditions (2) during tunneling the
evanescent and anti-evanescent waves with
kx=
cko) one can use the same form of time
operator, as for particles in non-relativistic quantum mechanics – and
therefore to show the equivalence of calculations for <t(x)>, variance Dt(x) etc in both time and energy
representations. Òhen for wave
packets like in Fig.1 for the boundary conditions (2) during tunneling the
evanescent and anti-evanescent waves with
kx=![]() = ± i
= ± i![]() em appear. Results (6)-(10)
expand the results of [8] for particle tunneling which were recognized to be
the best in Copenhagen quantum theory in [10].
em appear. Results (6)-(10)
expand the results of [8] for particle tunneling which were recognized to be
the best in Copenhagen quantum theory in [10].
In the cases of fluxes which signs are
changing we, following [8,11], can introduce quantities Jem,x, ± = =Jem,x×![]() ( ± Jem,x ) with the same physical sense, as for particles. And then the
expressions for mean values and variances of time distributions for moving,
tunneling and reflection were obtained in the same way, as for non-relativistic
particles in quantum mechanics.
( ± Jem,x ) with the same physical sense, as for particles. And then the
expressions for mean values and variances of time distributions for moving,
tunneling and reflection were obtained in the same way, as for non-relativistic
particles in quantum mechanics.
In particular case of quasi-monochromatic
wave packets one, using the stationary phase method for particles [12] (when |ki (![]() )|2d
)|2d![]()
![]() (
(![]() ) ) can obtain the similar expression for the phase tunneling time (that is defined in
the approximation of the stationary phase)
) ) can obtain the similar expression for the phase tunneling time (that is defined in
the approximation of the stationary phase)
![]() Ph tun,em = 2/c
Ph tun,em = 2/c![]() em for
em for ![]() em L >>1. (11)
em L >>1. (11)
From (11) one can see that
if ![]() em L > 2, the effective tunneling velocity
em L > 2, the effective tunneling velocity
vefftun = L /![]() Phtun,em (12)
Phtun,em (12)
exceeds c, i.å. is superluminal. It is a particular case
of the Hartmann phenomenon which was firstly
revealed and studied in [8,13] for 1-D motion of quasi-monochromatic particles,
tunneling through potential barriers. Concretely it ñînsists in the independency of phase tunneling time on the width of sufficiently wide barrier. This
result is consistent with the experimental data [3] for photons.
One can see that for “photonic
barriers” electromagnetic waves and photons are tunneling through them
similarly to particle tunneling through potential barriers. Tunneling of the classic evanescent electromagnetic waves firstly was studied experimentally in [14] with the
utilization of the two-prism scheme (like depicted in Fig.3b). Such barriers
were constructed for the study of the electromagnetic-waves propagation in the
microwave range through the wave-guides (see Fig.2), in the optical range
through devices with the frustrated total reflection (see Fig.3) etc. Further,
from [15-19] there are known the
results of the optical experiments with tunneling of photons (see the schema
from [17], represented in
Fig.3à). In Fig.3b there is
represented the device with two prisms exhibits the space shift of reflected
and transmitted beams with regard of that is expected from the geometric optics
[19].
Finally, there are appeared also the
experimental works on the study of the generalized Hartmann phenomenon for two
barriers ([20,21]). They were performed for the motion (out of the resonances)
of the electromagnetic waves in the microwave range through the wave-guards
[22] (see Fig.4), as well as for the optical photons in the fibrous optics
[23]. Since the tunneling in the both cases was in the region of frequences,
far from resonances, the general phase tunneling time was appeared to be
independent not only from the barrier widths but also from the distances between the barriers.
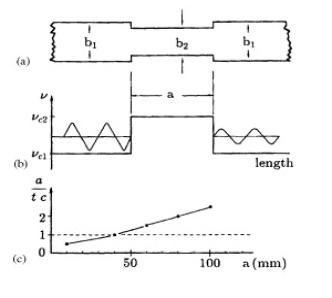
Fig.2. On this scheme there is represented one
of the experimental results of Nimtz from [3], accordingly to which the mean
velocity of the transmission by the beam of narrow segment exceeds the light
velocity ñ for the sufficiently long “photon barriers”.
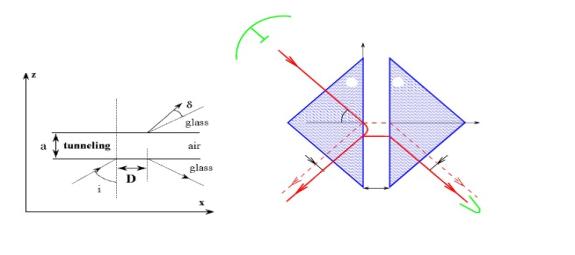
(à) (b)
Fig.3. (à) The violated total internal
reflection and tunneling of evanescent waves. (b) Later scheme from [18],
considering effect of Goose-Hanchen.

Fig.4. Tunneling of the electromagnecic waves of the microwave range
through two narrow segments.
III. The problem of the physical interpretation for the superluminal tunneling velocities of photons. The phenomena of
superluminal velocities, observed in the experiments with photon tunneling and
evanescent electromagnetic waves [3,15-19] and in number of further works, generated the series of discussions
on the relativistic causality, as well as in [3,8,15-19,22-27]etc. Up to now the consensus of
the discussion results is not achieved. They are continuing, as well as also
the experiments are continuing (see, for instance, [28-30]). Usually now such
interpretations of the superluminal tunneling photons are discussed:
1) The interpretation o the superluminal group velocities of tunneling photons without violations of causality or special relativity theory was proposed in [15], started from the reformation (or reconstruction) in the impulse attenuation: later parts of the incoming impulse are attenuated
stronger, so in the result the out-coming impulse is shifted to the front
parts, effectively intensifying them (and so effectively increasing the group
velocity) strictly by causal way. Such scheme is quite compatible with the usual idea of causality (see, for instance, [8]: If the total impulse attenuation is very great and during tunneling the leading part of the pulse is attenuated more less than the cord part, then the time envelope of exit small flux can be completely placed under the initial time envelope of the incoming pulse.
2) It deserves the separate payment the curious idea of “super-oscillations”, proposed in [31].
3) In principle the presence of
the superluminal phenomena it is possible, at least partially, to explain also
by the non-locality of the barriers, connected with the simultaneous change of
the space-time metrics in total inside all the barrier range where energies of
incoming wave packets do not succeed the barrier height (more details see in [25,32]).
IV.
1-D tunneling. Ànalysis of multiple internal
reflections for the 1-D potentials with the barriers is carrying out during the
sufficiently long time (see, for instance, [33-37]). This problem is trivial
for the attractive potentials and over-barrier energies inside barriers. And
the situation is sharply changing for the under-barrier energies, that is when
there is tunneling. In this case evanescent and anti-evanescent waves appear
and separately have zero fluxes. To
non-zero fluxes there are correspondent only linear combinations of evanescent
and anti-evanescent waves together.
For correct
analysis of multiple successive reflections from the internal barrier walls
during tunneling through it, we shall use the formalism with time analysis of
tunneling processes, elaborated in [8], considering also the results of [33-37].
We limit ourselves by the simplest case of the rectangular barrier of the
height V0 in the interval
(0, à) along axis x, and the tunneling evolution we shall
describe by the non-stationary picture of the actually moving wave packets, ñînstructed from the stationary plane waves and being
rid of the over-barrier energies by the additional transformation ![]() ®
®![]() Q(E–V0) (where Q(E–V0) is the step Heavyside
function). Instead of the usual sewing of the stationary wave functions in
points x = 0 and x = a for findings of the
analytic expressions for AR
, AT , a and b , we pass to the
analysis of the transmission of the initial wave packet through the first wall
of the potential barrier, (1) without considering the influence of the second
(final) wall of the potential barrier, since the wave packet is not still
reached it due to the finite motion velocity, (2) without the violation of the
demand of the finiteness for the wave packets in the case of the infinitely
wide barriers (since the growing anti-evanescent waves are no introducing still
at all), (3) constructing the wave packets by the following steps of the
multiple internal reflections in such a way that they were analytic continuation of the appropriate expressions,
corresponding to the current waves for
the over-barrier energies.
Q(E–V0) (where Q(E–V0) is the step Heavyside
function). Instead of the usual sewing of the stationary wave functions in
points x = 0 and x = a for findings of the
analytic expressions for AR
, AT , a and b , we pass to the
analysis of the transmission of the initial wave packet through the first wall
of the potential barrier, (1) without considering the influence of the second
(final) wall of the potential barrier, since the wave packet is not still
reached it due to the finite motion velocity, (2) without the violation of the
demand of the finiteness for the wave packets in the case of the infinitely
wide barriers (since the growing anti-evanescent waves are no introducing still
at all), (3) constructing the wave packets by the following steps of the
multiple internal reflections in such a way that they were analytic continuation of the appropriate expressions,
corresponding to the current waves for
the over-barrier energies.
Thus we consider three successive steps in
the tunneling evolution:
The
first step: A particle initiates the tunneling process through the barrier with
the intersection of the first barrier wall at x=0. In this initial step we
have the incoming wave packet in the region before the barrier
Yin (x, t) = ![]() dEg(E)yin(x, k)exp(–iEt/
dEg(E)yin(x, k)exp(–iEt/![]() ), x< 0 , (13)
), x< 0 , (13)
plus the wave
packet, reflected from the first barrier wall,
![]() (x, t) =
(x, t) = ![]() dEg(E)
dEg(E)![]() (x, k)exp(–iEt/
(x, k)exp(–iEt/![]() ), x<
0 . (14)
), x<
0 . (14)
The sum of wave packets (13) and (14) does
continuously pass after transmission through the initial barrier wall into the
wave packet inside the barrier. Supposing the rectangular form and conserving
the hypothesis that the tunneling packet does not still feel the second barrier
wall, the penetrated under barrier wave packet firstly contains only evanescent
waves:
![]() (x, t) =
(x, t) = ![]() dEg(E)a 0 exp (–cx)exp(–iEt /
dEg(E)a 0 exp (–cx)exp(–iEt /![]() ), 0 < x < a
(15)
), 0 < x < a
(15)
[a0 is here the
coefficient of the initial penetration]. Further, from the sewing conditions of
the stationary wave functions in point x =
0 we obtain two linear non-homogeneous equations for the unknowns ![]() and a0. We underline that the stationary flux for a 0 exp (–c x) and the total
flux for
and a0. We underline that the stationary flux for a 0 exp (–c x) and the total
flux for ![]() (x, t), integrated over time, both are equal to 0.
(x, t), integrated over time, both are equal to 0.
The second
step: A particle passes the second barrier wall in point x = a. During the transmission the second
barrier wall after the penetration inside the barrier region the wave packet is
transformed two packets– (à) one - tunneled
and propagating inside the region and (b) two - reflected from the second
barrier wall and penetrating back in the same region. From the sewing of the
stationary wave functions in point x = a in the second step similarly to the
first step we obtain two linear non-homogeneous equations for the unknowns ![]() (the amplitude of the stationary
wave, transmitted through the second barrier outside and b0 (the amplitude of
anti-evanescent wave, reflected from the second wall inside the barrier).
(the amplitude of the stationary
wave, transmitted through the second barrier outside and b0 (the amplitude of
anti-evanescent wave, reflected from the second wall inside the barrier).
The third step: A particle, reflected back
from the second wall, passes again through the first wall, intersecting it,
moving in the direction of the negative semi-axis x. The wave packet, reflected
from the second wall, is going inside the barrier to the first wall. Then it
transforms in two packets - (à) transmitted
through this wall (in addition to the packet, reflected in the first step back
inside the barrier) and (b) reflected from the first wall forwards inside the
barrier. From the sewing of wave functions in point x = 0, as in the case of the first two steps, we obtain again two
linear non-homogeneous equations for the unknowns ![]() (the amplitude of the
stationary wave, transmitted through the first wall back in the region I) and a 1 (the amplitude of the
stationary evanescent wave, reflected from the first wall back in the region II). This third step corresponds
naturally to the first internal reflection. And the process of the second and
the third steps it is possible to iterate, taking into account the successful
processes of internal reflections of gradually decreasing (with the increasing
number of the previous internal impacts of particle with walls with the partial
exit trough the wall outside). Such description of the tunneling process
inevitably includes the approach of multiple
internal reflections [33-37]. It is easy to see that any of the further
steps can be reduced to one of the first three considered steps. Moreover, we
obtain from the demands of the continuity of the wave functions the following
recurrent relations
(the amplitude of the
stationary wave, transmitted through the first wall back in the region I) and a 1 (the amplitude of the
stationary evanescent wave, reflected from the first wall back in the region II). This third step corresponds
naturally to the first internal reflection. And the process of the second and
the third steps it is possible to iterate, taking into account the successful
processes of internal reflections of gradually decreasing (with the increasing
number of the previous internal impacts of particle with walls with the partial
exit trough the wall outside). Such description of the tunneling process
inevitably includes the approach of multiple
internal reflections [33-37]. It is easy to see that any of the further
steps can be reduced to one of the first three considered steps. Moreover, we
obtain from the demands of the continuity of the wave functions the following
recurrent relations
a0 =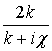 , bn = an
, bn = an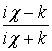 exp(–2ca), an+1 = bn
exp(–2ca), an+1 = bn 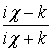 , (16)
, (16)
![]() =
=![]() ,
,
![]() = an
= an![]() exp (- ca–ika),
exp (- ca–ika), ![]() = bn
= bn![]()
for the unknowns an
,bn ,![]() and
and ![]() (n=0,1,…) in the all steps of the tunneling evolution of a wave
packet. The number n numerates the
sequential step of the wave-packet evolution inside the battier, beginning from
n=0 (starting from penetration of a
wave packet inside the barrier). For n
¹ 0 the number of the correspondent evolution step is
connected with the internal reflection from any barrier wall before the arrival
to another wall.
(n=0,1,…) in the all steps of the tunneling evolution of a wave
packet. The number n numerates the
sequential step of the wave-packet evolution inside the battier, beginning from
n=0 (starting from penetration of a
wave packet inside the barrier). For n
¹ 0 the number of the correspondent evolution step is
connected with the internal reflection from any barrier wall before the arrival
to another wall.
The uneven values n=2m+1 correspond to the reflections from the
first barrier wall (for am,) while the even
values n=2(n+1) cîrrespond to the reflections from the second barrier
wall (for an ).
The general evolution of a wave packet
tunneling through the barrier describes with the help of summing over all
possible steps. And one can easily see that
AT =![]() = 4ic k exp(–ca–ika)/F, AR
=
= 4ic k exp(–ca–ika)/F, AR
=![]() =
=![]() D– /F , (17)
D– /F , (17)
a =![]() = 2k(k+ic) / F ,
b =
= 2k(k+ic) / F ,
b =![]() = 2k(ic – k) exp(– 2c a) / F,
= 2k(ic – k) exp(– 2c a) / F,
where F=(k2–c 2)D– + 2ikcD+ , ![]() = 1± exp(–2ca),
= 1± exp(–2ca), ![]() = k2 + c 2 = 2mV0 /
= k2 + c 2 = 2mV0 /![]() .
.
All these results for a, b, AT and AR coincide with the results,
obtained in the standard sewing of the stationary wave function, which
satisfies the solution of the time-dependent Schroedinger equation ([37]). Moreover, after the changer ic® k1, where k1 = [2m(E–V0)]1/2/![]() is the wave number with the over-barrier energies (E>V0),
all the expressions (43) for a , b , AT and AR pass to those expressions of the same
quantities, which are obtained during the motion of the usual particles over
the barrier in the terms of the multiple internal reflections ([38]).
is the wave number with the over-barrier energies (E>V0),
all the expressions (43) for a , b , AT and AR pass to those expressions of the same
quantities, which are obtained during the motion of the usual particles over
the barrier in the terms of the multiple internal reflections ([38]).
The
intermediate and total tunneling and reflection times. Thus, considering multiple internal reflections, we shall study the phase times for the
quasi-monochromatic wave packets (39)-(40), following [38], and in the result
we obtain: tin = ![]() for the initial wave
packet in the barrier beginning (x=0)
– we choice it for the initial (zero) time;
for the initial wave
packet in the barrier beginning (x=0)
– we choice it for the initial (zero) time;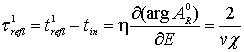 (where v =
(where v = ![]() k/m is the group initial velocity) is the
phase time of the external reflection in the first step; and
k/m is the group initial velocity) is the
phase time of the external reflection in the first step; and 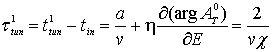 is the phase tunneling time in
the first step (x =a).
is the phase tunneling time in
the first step (x =a).
Similarly we obtain such expressions for
the reflection and tunneling times for n-th
step [37]: , n =n +1, n =0,1,…, 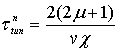 , n = 2m +1, m =0,1,…. And finally, the phase times of total
tunneling and reflection are defined [37]: ttun =
, n = 2m +1, m =0,1,…. And finally, the phase times of total
tunneling and reflection are defined [37]: ttun = 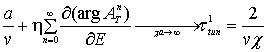 , trefl =
, trefl =![]() =ttun
=ttun 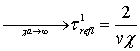 . Evidently, not only ttun , but also all
. Evidently, not only ttun , but also all ![]() (n =1,2,…) manifest the Hartmann phenomenon.
(n =1,2,…) manifest the Hartmann phenomenon.
Taking into account
the similarity of the photon and particle motion, studied in [8], we can extend
the obtained results on the photon 1-D penetration and tunneling.
V. 2-D
tunneling: Introduction. One-dimensional
(1-D) penetration and tunneling of the non-relativistic particles and photons
through the potential barrier was studied in the stationary and non-stationary
approaches in a lot of references (see, for instance, [8,33-37]). Here we shall
describe, following [38], in the quasi-monochromatic approximation the motion
of the non-relativistic particles by use of the stationary 2-D Schroedinger
equation
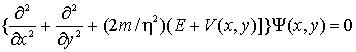 (18)
(18)
where ![]() is the stationary
wave function, m is the particle
mass,
is the stationary
wave function, m is the particle
mass, ![]() is the potential (barrier) and E
is the total energy. The regions I and II are defined as the regions with zero
potentials V(x) = V(y) = 0 (I for –¥ < x £ 0 , –¥ < y < ¥ and II for a £ x< ¥, –¥ <y<¥). The region III ñontains the barrier V(x) = =V0 >0, and V(y)
= 0 (0 £ x < ¥ ,–¥ < y < ¥). All three regions are
infinite along the axis y (in
parallel to the interfaces between I and II, and also between II and III). There
is the translational symmetry along the axis y in all three regions (since V(y)=0 everywhere).
is the potential (barrier) and E
is the total energy. The regions I and II are defined as the regions with zero
potentials V(x) = V(y) = 0 (I for –¥ < x £ 0 , –¥ < y < ¥ and II for a £ x< ¥, –¥ <y<¥). The region III ñontains the barrier V(x) = =V0 >0, and V(y)
= 0 (0 £ x < ¥ ,–¥ < y < ¥). All three regions are
infinite along the axis y (in
parallel to the interfaces between I and II, and also between II and III). There
is the translational symmetry along the axis y in all three regions (since V(y)=0 everywhere).
The study of 2-D penetration and tunneling quasi-monochromatic non-relativistic
particle through the potential barrier. In the stationary scheme (see Fig.5)
the incident plane wave ![]() with
with ![]() = {kx , ky},
= {kx , ky}, ![]() ={x, y},
={x, y}, ![]() ,
, ![]()
![]() and with total energy
(which is kinetic energy in I and III) E =
and with total energy
(which is kinetic energy in I and III) E =![]() +
+![]() , describing in I a free particle, moving in the direction to point (x=y=0).Let
us analyze over-barrier penetration with Ex
> V0 .In
point (x=y=0) there is appears the first externally reflected plane wave
, describing in I a free particle, moving in the direction to point (x=y=0).Let
us analyze over-barrier penetration with Ex
> V0 .In
point (x=y=0) there is appears the first externally reflected plane wave ![]()
![]() , where
, where![]() is the amplitude of the first reflection from the left
boundary of the interface in I,
is the amplitude of the first reflection from the left
boundary of the interface in I, ![]() ={–
={–![]() ,ky},
and the first transmitted (in II) wave
,ky},
and the first transmitted (in II) wave ![]() , where
, where![]() is the amplitude of the first penetration (in II),
is the amplitude of the first penetration (in II), ![]() ,
,![]() . Further, in the first point of exit (x=a, y = Dy), Dy is the first
shift upstairs in II (due to the motion with ky along the axis y),
appears the first traversed plane wave
. Further, in the first point of exit (x=a, y = Dy), Dy is the first
shift upstairs in II (due to the motion with ky along the axis y),
appears the first traversed plane wave ![]() , where
, where![]() is the amplitude of the first traversed (in II) wave, and
the first reflected (inside II) wave
is the amplitude of the first traversed (in II) wave, and
the first reflected (inside II) wave![]() , where
, where ![]() is the amplitude of the first
reflected (inside II) wave,
is the amplitude of the first
reflected (inside II) wave, ![]() .The shift Dy evidently can
be defined as
.The shift Dy evidently can
be defined as
Dy = a tan![]() , tan
, tan![]() =
= ![]() , (19à)
, (19à)
or
Dy=(![]() = a tan
= a tan![]() ,
(19b)
,
(19b)
where![]() =am/ħ
=am/ħ![]() is the phase time of particle motion along the distance a with the velocity
is the phase time of particle motion along the distance a with the velocity ![]() (i.å. the time of passing of the quasi-monochromatic
particle along the axis x in II from
point x=0 till point x=a, defined in the approximation of the
stationary phase).
(i.å. the time of passing of the quasi-monochromatic
particle along the axis x in II from
point x=0 till point x=a, defined in the approximation of the
stationary phase).
Further, in point (x=0, y=2Dy) there is appears the second transmitted (in II)
wave, or the second reflected inside (from the left boundary of interface II)
wave![]() , where
, where![]() º
º![]() is the amplitude of the second transmitted (in II) wave, or , which all
the same, the second internally reflected (from the left boundary of the
interface II) wave, and the second externally reflected (in I) wave
is the amplitude of the second transmitted (in II) wave, or , which all
the same, the second internally reflected (from the left boundary of the
interface II) wave, and the second externally reflected (in I) wave![]() , where
, where![]() is the amplitude of the second externally reflected (in I) wave. Etc
etc... (it can be continued till the arbitrary n-th externally reflected (in I) wave
is the amplitude of the second externally reflected (in I) wave. Etc
etc... (it can be continued till the arbitrary n-th externally reflected (in I) wave ![]() , n ³ 2).
, n ³ 2).
From the sewing conditions for waves and
their first derivatives ![]() in points (x=y=0),
(x=a, y=Dy), (x=0, y=2Dy), (x=a,
y=3Dy),…, we obtain
(neglecting by the plane wave exp(i
in points (x=y=0),
(x=a, y=Dy), (x=0, y=2Dy), (x=a,
y=3Dy),…, we obtain
(neglecting by the plane wave exp(i![]() y)):
y)):
![]() =
=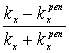 ,
,![]() =
=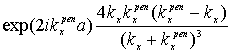 ,
,
![]() =
=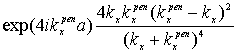 ,…,
,…,![]() =
=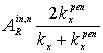 (n=1,2,…), (20)
(n=1,2,…), (20)
![]() =
=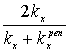 ,
,![]() =
=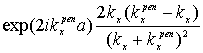 ,
,![]() =
=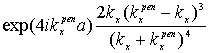 ,…,
,…,![]() =
=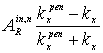 (n=1,2,…), (21)
(n=1,2,…), (21)
![]() =
=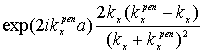 ,
,![]() =
=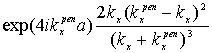 ,
,![]() =
= 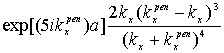 ,…,
,…,![]() =
=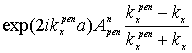 (n=1,2,…), (22)
(n=1,2,…), (22)
![]() =
=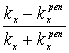 ,
,![]() =
=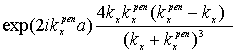 ,
,![]() =
= 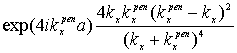 ,…,
,…,![]() =
=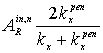 (n=1,2,…), (23)
(n=1,2,…), (23)
![]() =
=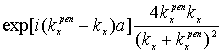 ,
,![]() =
=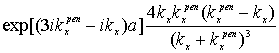 ,
,![]() =
=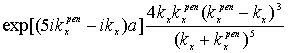 ,…,
,…,
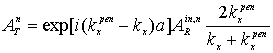 (n=1,2,…). (24)
(n=1,2,…). (24)
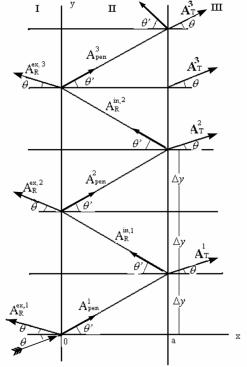
I
II III
Fig.5 The schematic picture of the multiple 2D reflections, over-barrier
penetrations and transmissions of non-relativistic particles.
In the case k=![]() , when q=0 (see Fig.5) i.å. the incident plane wave is perpendicular to the first boundary of interface and Dy=0, it is not difficult to see that
, when q=0 (see Fig.5) i.å. the incident plane wave is perpendicular to the first boundary of interface and Dy=0, it is not difficult to see that 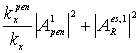 =1 and
=1 and ![]() , due
to the conservation of the flux in the first transmission through points (x=y=0) and (x=0, y=a). In the case of 1-D penetration (at q =0, when the incident plane wave is perpendicular to the first boundary of interface and Dy=0) all expressions, including the last expressions n=1,2,…, in (20)-(24) are coincident with the correspondent 1-D expressions in [37], represented with
the help of the time analysis (for the stationary phase) to the 1-D tunneling.
, due
to the conservation of the flux in the first transmission through points (x=y=0) and (x=0, y=a). In the case of 1-D penetration (at q =0, when the incident plane wave is perpendicular to the first boundary of interface and Dy=0) all expressions, including the last expressions n=1,2,…, in (20)-(24) are coincident with the correspondent 1-D expressions in [37], represented with
the help of the time analysis (for the stationary phase) to the 1-D tunneling.
Now let analyze sub-barrier tunneling at Ex<V0. If the angle q is sufficiently
large (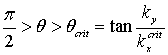 , where
, where ![]() is defined by eq.
is defined by eq. ![]() =V0), then
=V0), then ![]() < V0 and the values of
< V0 and the values of ![]() are imaginary, i.å.
are imaginary, i.å. ![]() = ic with c >0 and there is sub-barrier tunneling,
= ic with c >0 and there is sub-barrier tunneling, ![]() . In this case, instead of over-barrier penetration, for
description sub-barrier tunneling it is necessary introduce c instead of
. In this case, instead of over-barrier penetration, for
description sub-barrier tunneling it is necessary introduce c instead of ![]() with the help of substitution
with the help of substitution ![]() =ic. And instead of current
(in II) waves
=ic. And instead of current
(in II) waves ![]() , the evanescent an
, the evanescent an![]() and anti-evanescent wavesbnexp(gx) will appear. The correspondent picture is
represented in Fig.6.
and anti-evanescent wavesbnexp(gx) will appear. The correspondent picture is
represented in Fig.6.
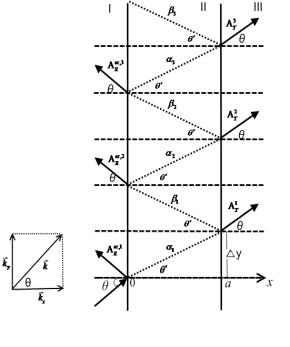
Fig.6.The schematic description of the multiple
2-D reflections, sub-burrier penetrations and transmissions of a
non-relativistic particle.
In
this case factually utilized the analytic continuation from the region of real
(over-barrier) wave numbers to the region of imaginary (under-barrier) wave
numbers similarly to that was made in [37]. The obtained results, like to
(20)-(24) but with substitutions ![]() ® ic,
® ic, ![]() ®
®![]() ,
, ![]() ®
®![]() coincide with the correspondent 1-D results in [37].
coincide with the correspondent 1-D results in [37].
Instead of the shift Dy along the axis y, defined for the above-barrier
transmission by equations (19a) and (19b) and depicted in Fig.5, it is
necessary to use the expressions, like (19b):
Dn y=(![]() , (19ñ)
, (19ñ)
where
![]() =
=![]()
![]()
![]()
![]() (n=1,2,…),
(25)
(n=1,2,…),
(25)
and
![]() (n=1,2,…). (26)
(n=1,2,…). (26)
The quantities ![]() è
è ![]() represent the phase times of
motion (i.å. the times of moving for a
quasi-monochromatic particle in the approximation of the stationary phase) for
the n-th step at the under-barrier
tunneling through point x=a and the n-th step at the external reflection from the first barrier in
point x=0, respectively ([8]). Of
course, the shifts Dny with different
values of n=1,2,3,… are different
(due to the not large numerical increase of
represent the phase times of
motion (i.å. the times of moving for a
quasi-monochromatic particle in the approximation of the stationary phase) for
the n-th step at the under-barrier
tunneling through point x=a and the n-th step at the external reflection from the first barrier in
point x=0, respectively ([8]). Of
course, the shifts Dny with different
values of n=1,2,3,… are different
(due to the not large numerical increase of ![]()
![]()
![]() and
and ![]() for increasing numbers n, but they are always proportional to
2/vc in the limit ca ® ¥). Tunneled and
externally reflected waves of the increasing order with the increasing of
number n are quickly damped due to
the factor exp(–ca) in expressions
for
for increasing numbers n, but they are always proportional to
2/vc in the limit ca ® ¥). Tunneled and
externally reflected waves of the increasing order with the increasing of
number n are quickly damped due to
the factor exp(–ca) in expressions
for ![]() and
and![]() , and finally vanish.
, and finally vanish.
In [39] without the strict
theoretic justification and neglecting
the multiple internal reflections and transmissions (instead of analytic
continuation, used in [33-37]) there was used only
one usual linear combination of waves ![]() for the kx – component inside the
region II and only one wave
for the kx – component inside the
region II and only one wave ![]() for ky –component inside the
region II, and there was obtained the following expression for only one shift along axis y in the second boundary of interface
(between II and III)
for ky –component inside the
region II, and there was obtained the following expression for only one shift along axis y in the second boundary of interface
(between II and III)
Dy =(![]() (19d)
(19d)
which is
represented in Fig.7, when
![]() =ttun=a/v+h¶argAT/¶E=(vc)-1 for
ca®¥ (27)
=ttun=a/v+h¶argAT/¶E=(vc)-1 for
ca®¥ (27)
with AT=![]() ,
,![]() ,
, ![]() , , and in the result
there was obtained only one
transmitted (in III region) 2-D wave
, , and in the result
there was obtained only one
transmitted (in III region) 2-D wave![]()
![]() which is moving in the parallel direction to the incident
wave.
which is moving in the parallel direction to the incident
wave.
Thus, we have confronted two approaches
for 2-D sub-barrier tunneling for the sub-barrier tunneling of a particle. The
first one is represented in Fig. 6 with the infinite series of internal
reflections and transmitted waves – with the help of formulas (20)-(24), with changing
![]() ® ic,
® ic, ![]() ®
®![]() ,
, ![]() ®
®![]() and with the help of shifts (19c,d). The second one is
represented in Fig.7 with the only one shift
during tunneling and the înly one transmitted wave, which
is moving in parallel to the incident wave, in total neglecting by the multiple
internal reflections and the correspondent transmitted waves.
and with the help of shifts (19c,d). The second one is
represented in Fig.7 with the only one shift
during tunneling and the înly one transmitted wave, which
is moving in parallel to the incident wave, in total neglecting by the multiple
internal reflections and the correspondent transmitted waves.
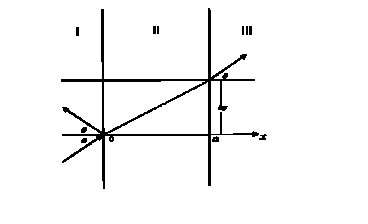
Fig.7. The scheme of 2-D tunneling with one
reflected and one transmitted wave.
Both approaches
indicate to the non-local behavior of the sub-barrier tunneling which brings to
the Hartmann phenomenon for the phase tunneling time in the limit ca ® ¥. This phenomenon
consists in the independence of the phase tunneling time on the barrier width ([8]).
And it remains only to confirm what from approaches really describes the
sub-barrier tunneling. Till now our approach is confirmed (Fig.6) by several
methods, described in [38], and preliminary is verified by rather old (however
without the real data processing) experimental observations, published in [40-41].
2-D
penetration and tunneling of a photon through the barrier. With taking into
account the similarity of the photon and particle motion we can extend the
obtained results on the photon 2-D penetrations and tunneling. Fig.5-7 can be
also used for photons, propagating in the homogeneous glass medium I and III,
penetrating or tunneling through the homogeneous air layer. In this case the
quantity
![]() (28)
(28)
is the refraction
light coefficient in the glass (if one suppose that the refraction light
coefficient in air is 1), and in Fig.6 it is described the penetration of
photons through the layer II for the angles lesser the critical angle 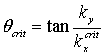 , i.å. than the angle of
the total internal reflection for incident photons, polarized perpendicularly
to the plane x-y of the light
incidence.
, i.å. than the angle of
the total internal reflection for incident photons, polarized perpendicularly
to the plane x-y of the light
incidence.
Fig.6 and 7 describe the violated total
internal reflection of the polarized light, tunneling through the slab II, for
the incidence angle ![]() (violated in the
sense of the partial transmission through the layer II in the glass medium III)
in both approaches, using 2-D tunneling for particles with the multiple
internal reflections, represented here (and also in some different form for the
light in [40-41]) (Fig.6), or using the description of the 2-D tunneling of the
non-relativistic particle and photon, represented in [39] (Fig.7). We hope that
the correct final refined optical experiments can give the clear demonstration
of the multiple internal reflections and multiple transmitted waves, as it was
previously analyzed in [40-41].
(violated in the
sense of the partial transmission through the layer II in the glass medium III)
in both approaches, using 2-D tunneling for particles with the multiple
internal reflections, represented here (and also in some different form for the
light in [40-41]) (Fig.6), or using the description of the 2-D tunneling of the
non-relativistic particle and photon, represented in [39] (Fig.7). We hope that
the correct final refined optical experiments can give the clear demonstration
of the multiple internal reflections and multiple transmitted waves, as it was
previously analyzed in [40-41].
VI. The
3-D tunneling.
One can enter upon such problem in a simple way, naturally extending the 2-D
problem of tunneling (for axes õ and ó) in the 3-D one(in axes õ, ó and z) and supposing the
surfaces of the interface to be 2-D (parallel to the plane of axes ó and z) with the previous direction of
tunneling along the axis õ. Leaving this
problem to the opinion of readers, we can also pass to the spherically
symmetrical tunneling problem, where the main role is placed to the radial
coordinate. Such problem is usually exposed not only in many monographs on
quantum mechanics, but even in almost all contemporary articles on nuclear
physics in the limits of WKB-approximation. Only in [42] this 3-D spherically
symmetric problem had been exposed in the limits of the self-consistent quantum
mechanics.
VII.
Summary and further
perspectives.
1) So, here there
was studied, basing on similarity of particle and photon tunneling, the
theoretic results of 2-D and 3-D photon tunneling and multiple internal
reflections. Then there are proposed the refined optical experiments for these
phenomena in the continuation of [40-41].
2) There is remained
an interesting perspective to resolve the problem of the signal superluminality of the modulated waves in the
electromagnetic (photon) tunneling in addition to the resolved group-velocity
superluminality in the photon tunneling.
References
1.A.I.Akhiezer, V.B. Berestezki, Quantum
Electrodynamics, FM, Moscow, 1959 [in Russian].
2. S.Schweber, An Introduction to
Relativistic Quantum Field Theory, Row, Peterson &Co,Evanston, Ill, 1961
(chapter 5.3).
3. A.Enders, G.Nimtz, J.Phys.I
(France) 2 (1992)1693; J.Phys.I (France) 3 (1993)1089; Phys.Rev.
B 47 (1993)9605; Phys.Rev. E 48(1993)632;
G.Nimtz, in: Tunneling and ist
Applications, World Sci., Singapore,
1997, pp.223-237.
4. J.D.Jackson, Classical
Electrodynamics, Wiley, N.Y.,1975, section 8.3.
5. P.M.Morse, H.Feshbach, Methods
of Theoretical Physics,McGraw-Hill, N.Y.,1953 part II (chapter 13).
6. L. Brillouin, Wave Propagation
and Group Velocity, Academic Press, N.Y., 1960.
7. J.Jakiel, V.S.Olkhovsky, E.Recami, Phys.Lett.A 248 (1998)156-160.
8. V.S.Olkhovsky, E.Recami, Phys.Rep.
214 (1992)339; V.S.Olkhovsky, E.Recami,J.Jakiel, Phys.Rep.398 (2004)133.
9. L.B.Felsen, N.Marcuvitz, Radiation and Scattering of Waves,v.1,
Prentice-Hall, N.Y.,1973 (chapter1.5).
10. M.Abolhasani, M.Golshani, Phys.Rev., A62 (2000) 012106.
11. V.S.Olkhovsky,E.Recami,F.Racity,A.K.Zaichenko,J.Phys. (France)5 (1995)1351.
12. E.Wigner, Phys.Rev. 98 (1955)145.
13. T.E.Hartmann, J.Appl.Phys.33 (1962)3427.
14. J.Ch.Bose, Bose Institute
Transactions, 42 (1927).
15 A.M.Steinberg, P.G.Kwiat, R.Y.Chiao, Phys.Rev.Lett. 71 (1993)708; R.Y.Chiao, P.G.Kwiat, A.M.Steinberg, Scient.Am., 269:2 (1993)38.
16. Ch.Spielman, R.Szipoecs, A.Stingl,F.Krausz, Phys.Rev.Lett. 73 (1994)2308.
17. Ph.Balcou,L.Dutriaux, Phys.Rev.Lett.
78(1997)851.
18. V.Laude,P.Tournois, J.Opt.Soc.Am.
B16 (1999)194.
19. A.Haibel,G.Nimtz, A.A.Stahlhofen,Phys.Rev.E63 (2001)047601.
20. V.S.Olkhovsky, E.Recami, G.Salesi,Europhys.Lett. 57 (2002)879.
21. V.S.Olkhovsky, E.Recami, A.K.Zaichenko, Europhys.Lett. 70(2005)712.
22. G.Nimtz,A.Enders, H.Spieker, J.Phys.I
(France) 4 (1994)565.
23. S.Longhi,P.Laporta, M.Delmonte, E.Recami, Phys.Rev. E65 (2002) 046610.
24. R.Bonifaccio(ed.), Mysteries,Puzzles
and Paradoxes in Quantum Mechanics, AIP,Woodbury, N.Y., 1999, R.Y.Chiao
–pp.3-13; G.Nimtz –pp.14-31;E.Recami- pp.32-35; A.Steinberg- pp.36-46.
25. D. Mugnai, A.Ranfagni, L.S.Schulman (eds.),Time’s Arrows, Quantum Measurement and Superluminal Behavoir,
Napoli, Italy, Oct.3-5,2000 (C0nsiglio Nazionale delle Ricerche,Roma),
E.Recami-pp.17-36;G.Nimtz,A.Haibel,R.- M. Vetter- pp.125-138; V.S.Olkhovsky-
pp. 173-178.
26. G.Nimtz, Progress in Quantum
Electronics,27 (2003)417-450.
27. H.G.Winful, Phys.Rep. 436 (2006)1.
28. E.Recami, J.Phys.:Conf.Series
196;1 (2009) 012020.
29. G.Nimtz, Found.Phys.39:12(2009)1346-1355.
30. A.B.Shvartsburg, G.Petite, M.Zuev, J.Opt.Soc.Am.,B28(2011)2271-2276.
31. A.Aharonov, N.Erez,M.Reznik, Phys.Rev.
A65 (2002)052124.
32. F.Cardone, R.Mignani, V.S.Olkhovsky, Phys.Lett.,289 (2001)279; Mod.Phys.Lett.,14
(2000)109;J.Phys.I (France),7 (1997)1211.
33. J.H.Fermor, Am.J.Phys.,34 (1966)168.
34.R.W.McVoy,L.Heller and M.Bolsterli, Rev.Mod.Phys.,39 (1967)245.
35. A.Anderson, Am.J.Phys.,57 (1989)230.
36. S.P.Maydanyk, V.S.Olkhovsky, A.K.Zaichenko, J.Phys.Studies (Ukraine), 6 (2002)24.
37. F.Cardone, S.P.Maydanyk,
R.Mignani, V.S.Olkhovsky, Found.Phys. Lett., 19:5(2006)441.
38. V.S.Olkhovsky, M.V.Romanyk, J.Mod.Phys.,2:10
(2011)1166-1171, doi:110,4236/jmp.2011.210145.
39. A.M.Steinbergand R.Y.Chiao, Phys.Rev.,A49
(1994) 3283.
40. C.K.Carniglia and L.Mandel, J.Opt.Soc.Am.,61
(1971) 1035.
41. S.Zhu, A.W.Yu, D.Hawley and R.Roy, Am.J.Phys.,54 (1986)601.
42. V.S.Olkhovsky, V.Petrillo, J.Jakiel, W.Kantor, Central Eur. J. Phys.,6 (1) (2008)122 ; V.S.Olkhovsky, M.V.Romanyuk, Nuclear Physics
and Atomic Energy (Ukraine, Kiev),10,
N3 (2009)273.