Ю. В. Ващёнок, М.А. Мишенский, Ю. А. Гурвич

Белорусский национальный технический университет

Критерий для оценки нелинейных колебаний отдельных узлов транспортных средств

Когда логарифмический декремент колебаний остается постоянным для всего процесса затухающих или нарастающих колебаний отдельных узлов транспортных средств необходимо применять, критерий:

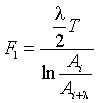, …, , (1)

где,– целые числа 1,2,3,…,.

Применимо к транспортному средству критерий F1 приобретает вид:

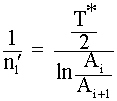(2)

F1- величина обратная коэффициенту n демпфирования (затухания) системы, одновременно оценивает своим числителем основное качество стабилизации (с учетом среднего времени реакции водителя), а знаменателем - тенденции к нарастанию или затуханию колебаний. Если знаменатель больше нуля, то имеет место колебательная устойчивость (затухание колебаний), если меньше нуля, то - колебательная неустойчивость (нарастание колебаний).

Для нелинейных колебаний отдельных узлов транспортных средств. Рекомендуется критерий:

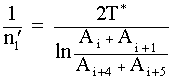(3)

Легко доказать (доказательство из-за простоты не приводится), что зависимость (3) идентична выражению (2)

Учет среднего времени реакции водителя в критерии F₁ существенно расширил область его применения. Теперь критерий может использоваться не только для точной оценки всех линейных колебаний управляемых колес, поведение которых характеризуется линеаризованными дифференциальными уравнениями движения, но и для более точной (по сравнению с критерием (2), тем не менее, приближенной (в определенном смысле осредненной величиной) оценки нелинейных колебаний.

0Оценка возможности критерия F1. Приведем два примера, в которых осуществляется анализ решений дифференциального уравнения движения груза на пружине при наличии демпфера:

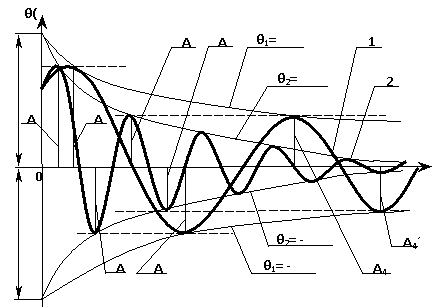
Рисунок 1. К оценке работы второго (2) и третьего (3) критериев

Приведём пример. С помощью критерия F₁ оценим два различных процесса затухающих колебаний, изображенных на рисунке 1. При одинаковых начальных условиях X_t=0 = X₀ , и различных сочетаний значений параметров С^'_1i и колебательной системы будем получать различные решения х_i = х_i(t), i = 1,n. Для решений х₁ =q₁ и х₂ = q₂, значения критерия F₄ будут составлять:

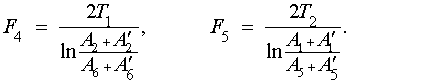
Знаменатели этих двух критериев равны, так как А₂ = А_{1 ,} А'₂ = А'_1, А₆ = А_{5 ,} А'₆ = А'₅. Числитель первого критерия больше, чем у второго. Следовательно, величина второго критерия меньше величины первого. Так как F₄ < F₅ , то процесс, отображаемый кривой 2, затухает быстрее, чем процесс 1.

Оценим возможности критерия F₁ на примере, в котором выполнен анализ решений линеаризованных дифференциальных уравнений движения управляемых колес. Здесь, как и в первом примере при одинаковых начальных условиях q_t=0 = q₀ и и различных совокупностях значений параметров описания шимми a_j, b_j, g_j, …, l_j; j = 1,k будем получать различные решения q_i = q_i(t), i =1,n. Выделенные три решения из n решений, изображены на рисунке 2. Для процессов 1 и 3 знаменатель критерия F₁, больше нуля. Поэтому в обоих случаях имеет место затухающий процесс - колебательная устойчивость. Для процесса 2 знаменатель критерия F₁ меньше нуля, что говорит о расходящемся процессе – колебательная неустойчивость. Минимальное значение критерия F₁ соответствует первому процессу.

Проанализируем те решения математического описания движения управляемых колес относительно шкворней, которые соответствуют их различным апериодическим движениям, и выберем из них наилучшее. Какой из апериодических процессов, изображенных на рисунке 2, является наилучшим?

На наш взгляд, наилучшим процессом будет тот, который для данного промежутка времени t - имеет:

- минимальную площадь под кривой q_i = q_i(t), i =1,3;

- минимальное значение ординаты q_1i в конце промежутка времени t.

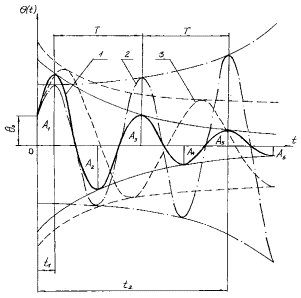
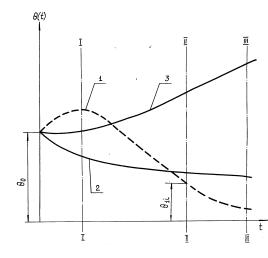
Рисунок 2 Рисунок 3

Для рассматриваемых в данном случае трех процессов ответы могут быть неоднозначными и даже противоречивыми. Все зависит от промежутка времени, на котором будут рассматриваться эти процессы. Например, если рассматривать процессы на промежутке времени от 0 до 1 (0-1), то наилучшая кривая - это кривая 2, а кривая 3 предпочтительнее первой. На промежутке времени 0-II третья кривая - наихудшая. Ее необходимо вообще исключить из дальнейшего рассмотрения. На промежутке времени, равном 0-III, у кривой 1 величина q₁₁ меньше, чем у кривой 2 ( q₁₁ < q₁₂ ) , но зато площадь под кривой 1 меньше, чем под кривой 1 и т.д.

Анализ колебаний управляемых колес различных машин показал, что при выборе промежутка времени, на котором сравниваются апериодические движения управляемых колес, необходимо руководствоваться еще и психофизическими возможностями водителя (т.е. временем его реакции и степенью утомляемости) .