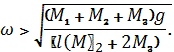Исследование рабочих процессов движения тел

по гладкой поверхности

Колола А.С., Лебедев Е. П., Рында О.С., Гурвич Ю.А.

Белорусский национальный технический университет, Минск

Движения тел по гладкой поверхности рассмотрим на примере движения электродвигателя массы М1, на валу мотора под прямым углом закреплен одним концом однородный стержень длины 21 и массы М2, на другой конец стержня насажен точечный груз массы M3, угло­вая скорость вала равна ω.

Определим горизонтальное дви­жение мотора, наибольшее горизон­тальное усилие R, действующее на болты, если ими будет закреплен кожух элек­тромотора на фундаменте.

 Покажем на рисунке 1 силы тяжести каждой части мотора — и суммарную реакцию  фундамента.

1) Если мотор не закреплен на фундаменте, то при движении стержня с точечным грузом корпус электромотора начнет движение, обозначим его перемещение Х и запишем координату центра масс по оси х:

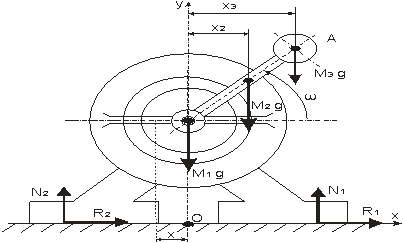
Рисунок 1 – Силы, действующие на электродвигатель.

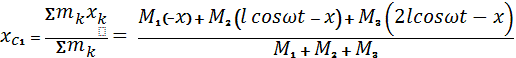,                  (1)

 

Если стержень с точечным грузом займет вертикальное положение, то координата центра масс по оси х будет

Так как проекция главного вектора внешних сил на ось х равна нулю, то согласно следствию из теоремы о движении центра масс можно записать. Приравняв выражение (1) к нулю, найдем х (горизонтальное движение мотора:

,

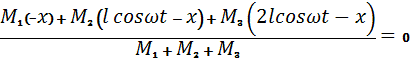или

откуда

.

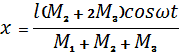В этом случае мотор совершает гармонические коле­бания с амплитудой А и периодом Т                 

      Если мотор закреплен на фундаменте, то на болты действует срезывающее усилие .

Найдем координату центра масс:

,

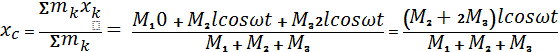и проекцию ускорения центра масс на ось x:

.                                                                     (2)

Запишем теорему о движении центра масс механической системы в проекции на ось х: 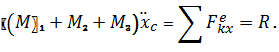                                                     (3)

Подставим выражения (1) в формулу (3) и получим:

Значение R будет наибольшим, когда , т.е.

.

Используя данные формулы определим массу всей системы :

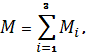
Координаты центров масс по оси у:

Тогда

Используем теорему о движении центра масс механической системы в проекции на ось у: 

С учётам выражений (4) запишем

Откуда

.

Наименьшим давление будет при  = 1, т.е.

.

Электромотор будет подпрыгивать при Nmin< 0:

Тогда получим