Ю. В.
Ващёнок, М.А. Мишенский, Ю. А. Гурвич
Белорусский национальный технический университет
Критерии
обеспечивающие оценку колебательных движений управляемых колес
Известно,
что одним из средств борьбы с колебаниями упругих конструкций служат
специальные покрытия, способные к интенсивному поглощению энергии колебаний.
Эффективность применения на практике того или иного покрытия определяется
логарифмическим декрементом колебаний. Логарифмический декремент колебаний
используется для характеристики интенсивности затухания. Пусть Т - условный
период затухающего колебания, Аi и Ai+1 - амплитуды значений
функции x(t) для двух ее последовательных экстремумов. Величина D,
равная:
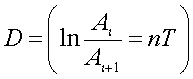 , (1)
, (1)
 называется логарифмическим декрементом
колебаний. Этот критерий широко используется во многих областях науки и
техники, например: при проектировании всех транспортных средств (самолетов,
вертолетов, автомобилей и т.д.); на стадии проектирования звукоизолирующих
перегородок в промышленных и гражданских зданиях. Ю. К. Фавстов (доктор
технических наук, профессор Самарского государственного технического
университета) экспериментально обнаружил парадоксальное явление, заключающееся
в том, что покрытия, материал которых характеризуется большим значением критерия
D, зачастую хуже демпфируют колебания, чем покрытия с меньшим значением этого
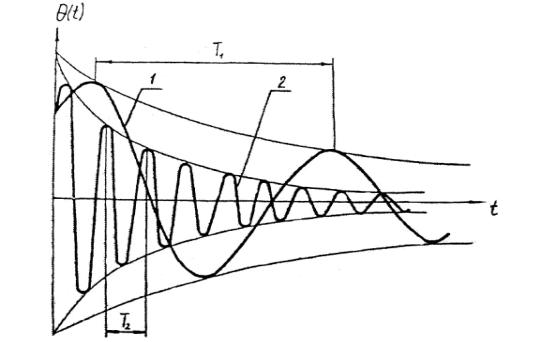
критерия. При рассмотрении виброграммы, приведённой на рисунке 1, можно сделать вывод: процесс,
соответствующий кривой 1 затухает медленнее процесса, соответствующего
кривой 2, хотя логарифмический
декремент в первом случае больше, чем во втором. Для исследований различного
рода колебательных процессов было разработано два семейства новых прикладных
критериев колебательной устойчивости-неустойчивости движения, которые свободны от
всех указанных недостатков.
называется логарифмическим декрементом
колебаний. Этот критерий широко используется во многих областях науки и
техники, например: при проектировании всех транспортных средств (самолетов,
вертолетов, автомобилей и т.д.); на стадии проектирования звукоизолирующих
перегородок в промышленных и гражданских зданиях. Ю. К. Фавстов (доктор
технических наук, профессор Самарского государственного технического
университета) экспериментально обнаружил парадоксальное явление, заключающееся
в том, что покрытия, материал которых характеризуется большим значением критерия
D, зачастую хуже демпфируют колебания, чем покрытия с меньшим значением этого
критерия. При рассмотрении виброграммы, приведённой на рисунке 1, можно сделать вывод: процесс,
соответствующий кривой 1 затухает медленнее процесса, соответствующего
кривой 2, хотя логарифмический
декремент в первом случае больше, чем во втором. Для исследований различного
рода колебательных процессов было разработано два семейства новых прикладных
критериев колебательной устойчивости-неустойчивости движения, которые свободны от
всех указанных недостатков.
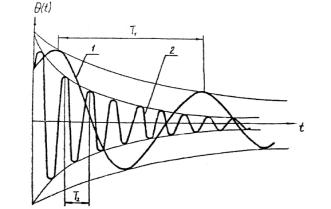
Рисунок 1 – Виброграммы
колебаний
При этом любой критерий из каждого семейства
критериев должен удовлетворять следующим требованиям: 1.Не противоречить теории
линейных колебаний: 1) Предлагаемый
критерий не должен противоречить логарифмическому декременту колебаний, с помощью
которого определяется темп затухания
любых колебаний. 2) Предлагаемый критерий будет аппроксимирован экспонентой в
связи с тем, что в основу логарифмического декремента колебаний положена экспоненциальная функция. 3) С помощью
предлагаемого критерия можно
оценить колебания управляемых колес
относительно шкворней с увеличивающейся амплитудой (нарастающие или расходящиеся колебания -
признак неустойчивости движения управляемых колес или склонности к
автоколебаниям колес, поведение которых описывается системой линеаризованных
дифференциальных уравнений движения).
2. Отражать основные свойства процесса стабилизации управляемых
колес. Предлагаемый критерий должен отразить основное качество
стабилизации, характеризуемое
временем возвращения повернутых
колес в нейтральное положение. 3.
Отличать “медленные” и “быстрые”
движения управляемых колес относительно шкворней. Чтобы понять, что под ними кроется,
рассмотрим пример. Допустим, что колебательная система, например управляемая
ось автомобиля, имеет логарифмический декремент колебаний D, равный 10.
Очевидно, что D=n*T = 10 можно получить бесчисленным числом способов сочетания
n и Т.(см.таблица 1). Из таблицы 1 (Таблица расчёта
логарифмического декремента) следует, что величину,
равную десяти, можно получить бесчисленным количеством способов. При
этом верхняя строчка таблицы и другие строчки, которые имеют большую величину
периода колебаний Т, соответствуют “медленному” движению управляемых колес. В
противном случае, все наоборот: нижняя строчка и другие строчки с маленьким
|
n |
T |
n*T |
|
0.1 0.2 . . . 50 100 |
100 50 . . . 0.2 0.1 |
10 10 . . . 10 10 |
значением периода Т
соответствуют “быстрому” движению управляемых колес.
Поэтому «медленными»
будем считать те колебания, у которых Т![]() n, а «быстрыми» — у которых, наоборот, n
n, а «быстрыми» — у которых, наоборот, n![]() Т.
Исходя из сказанного, в качестве первого семейства критериев предлагается величина, обратная коэффициенту
n демпфирования
(затухания) системы.
Т.
Исходя из сказанного, в качестве первого семейства критериев предлагается величина, обратная коэффициенту
n демпфирования
(затухания) системы.
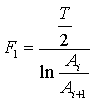 , …,
, …, 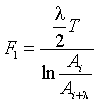 , (2)
, (2)
где![]() ,
,![]() –
целые числа 1,2,3,…,. Критерий F1 с
помощью величины, обратной обобщенному коэффициенту демпфирования колебательной
системы, одновременно оценивает своим числителем основное качество стабилизации
(с учетом среднего времени реакции водителя), а знаменателем - тенденции к
нарастанию или затуханию колебаний. Если знаменатель больше нуля, то имеет
место колебательная устойчивость (затухание колебаний), если меньше нуля, то -
колебательная неустойчивость (нарастание колебаний). В качестве второго
семейства критериев предлагается также величина, обратная коэффициенту n
демпфирования (затухания) системы.
–
целые числа 1,2,3,…,. Критерий F1 с
помощью величины, обратной обобщенному коэффициенту демпфирования колебательной
системы, одновременно оценивает своим числителем основное качество стабилизации
(с учетом среднего времени реакции водителя), а знаменателем - тенденции к
нарастанию или затуханию колебаний. Если знаменатель больше нуля, то имеет
место колебательная устойчивость (затухание колебаний), если меньше нуля, то -
колебательная неустойчивость (нарастание колебаний). В качестве второго
семейства критериев предлагается также величина, обратная коэффициенту n
демпфирования (затухания) системы.
КритерийF2 ( j
> i ).
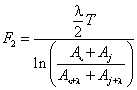 . (3)
. (3)
Если ![]() =
1, i = 1, j = 3, то
=
1, i = 1, j = 3, то
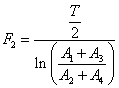 .
.
КритерийF5 ( m>l
> k > j > i ).
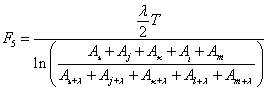 . (4)
. (4)
Если ![]() =
4, i = 2, j = 3, k = 4, l = 5, m=6, то
=
4, i = 2, j = 3, k = 4, l = 5, m=6, то
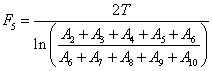 .
.
Второе
семейство критериев (3) – (4) может применяться и в тех случаях, когда
логарифмический декремент колебаний не является постоянной величиной для всего
процесса затухающих или нарастающих колебаний. Данные критерии обеспечивают
оценку колебательных движений управляемых колес транспортных средств.
Ликвидируя такой серьезный недостаток, как «парадокс» логарифмического декремента колебаний, критерии (2)…(4) улучшают
выходные характеристики транспортного средства на стадии его проектирования,
тем самым, способствуют управляемости и устойчивости, стабилизации и плавности
хода. При этом улучшается показатель безопасности движения.