Бобылёв А.С. Ващенок Ю.В. Гурвич Ю.А.

Белорусский национальный технический университет, Минск

Устойчивоть подпружиненного физического маятника методами Ляпунова

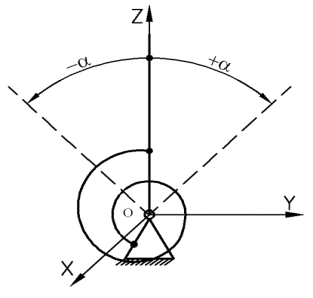
В отличие от существующих подходов определения устойчивости подпружиненного физического маятника, в данной работе анализ устойчивости маятника выполнен методами А.М. Ляпунова, что может оказаться полезным студентам, изучающим различные курсы, в которые входят разделы, связанные с анализом устойчивости различных систем. Постановка задачи. Положение равновесия физического маятника, в котором его центр масс находится над опорой неустойчиво. Для стабилизации этого положения между телом и опорой помещена спиральная пружина, создающая восстанавливающий момент М, пропорциональный углу наклона маятника α и равный М = сα, где с - жесткость пружины. Выполнить анализ устойчивости маятника методами А.М. Ляпунова.

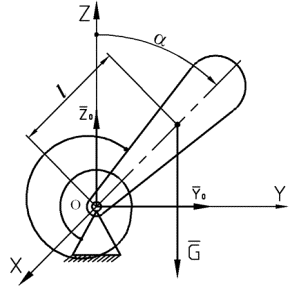
Рассмотрим физический маятник с осью привеса, совпадающей с осью вращения X, перпендикулярной плоскости чертежа и проходящей через точку О. Положение маятника будем определять углом α, отсчитываемого от вертикальной оси Z. Расстояние от оси привеса до центра масс маятника обозначим через l. На маятник, отклоненный от вертикального положения, действуют силы: G, Y₀, Z₀ и момент упругости пружины M. Трением в цилиндрическом шарнире пренебрегаем.

Определим кинетическую энергию маятника: , где J_x – момент инерции маятника относительно оси OX.

Для определения потенциальной энергии консервативных сил, приложенных к маятнику, рассмотрим три его положения:

- первое положение - вертикальное α₁=0, которое соответствует недеформированной спиральной пружине;

- второе и третье положения - ±α, соответствуют деформированной пружине.

Определим потенциальную энергию восстанавливающей силы спиральной пружины П₁ , П₂ , П₃ в трех положениях маятника при α₁ = 0, α₂ = + α, α₃ = – α.

,

,

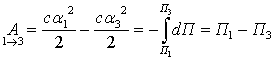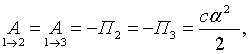
где - работа восстанавливающей силы пружины при перемещении ее конца вместе с маятником, соответственно, из положения 1 в положение 2 и из 1 в 3; = 0.

Потенциальная энергия сил, приложенных к маятнику, равна:

.

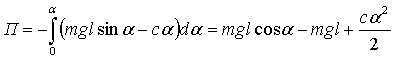Полная энергия системы:

.

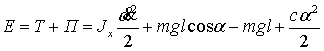Используя уравнение Лагранжа

,

составим дифференциальное уравнение движения маятника:

. (1)

Приведем уравнение (1) к двум дифференциальным уравнениям первого порядка. Обозначим через вещественные переменные параметры, характеризующие состояние физического маятника , .

,

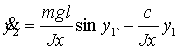. (2)

Тогда выражения (2) являются исходными уравнениями.

Одно из состояний равновесия физического маятника, расположенного вертикально при недеформированной пружине, характеризуются следующими значениями вещественных переменных . Поэтому уравнения возмущенного движения совпадают с исходными.

,

. (3)

Первый метод Ляпунова [1-3]. Разлагая в ряд Маклорена правые части уравнений возмущенного движения (3) по степеням и ограничиваясь членами первого порядка

малости, получим уравнения первого приближения:

,

. (4)

Запишем уравнения первого приближения в матричной форме:

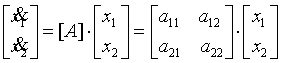или , (5)

где .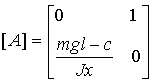

Составим характеристическое уравнение, соответствующее системе (5):

,

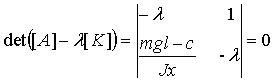где [K] - единичная матрица.

Характеристическое уравнение имеет вид: . Характер корней характеристического уравнения зависит от знака свободного члена:

§ Если , то этот знак положительный и корни характеристического полинома чисто мнимые 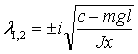. В соответствии с теоремой первого метода Ляпунова этот случай относится к критическому, т.к. вещественная часть корней равняется нулю (Re λ₁ = Re λ₂ = 0). Этот случай должен быть исследован дополнительно вторым методом Ляпунова.

§ Если , то свободный член отрицателен. Корни характеристического полинома вещественные и разных знаков. Они определяются по формуле .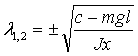

§ В соответствии с теоремой первого метода Ляпунова, при положительном значении одного из корней характеристического полинома, состояние равновесия неустойчиво независимо от нелинейных членов уравнения движения