Макаренко Р.Ю., Стульба М.А., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Выбор метода оптимизации при расчете количества вычислительных процедур при оптимизации методом сеток

Прежде чем приступить к выбору метода оптимизации, проанализируем с позиции существующую методику построения зон, областей или картин устойчивости либо неустойчивости движения управляемых колес на плоскости или в пространстве параметров по одному из критериев, например, скорости устойчивого движения колес. Для этого необходимо ответить на вопрос: в чем же выигрывает проектировщик, если одновременно варьировать два, три или более значений параметров при неизменных величинах остальных в математическом описании движения управляемых колес, по сравнению с изменением только одного параметра (при неизменном значении остальных)?

Ответ на поставленный вопрос получим после сравнения результатов вычислений по выведенным в этом разделе формулам, определяющим:

- количество совокупностей (или число сочетаний) значений параметров для n-мерного пространства варьируемых параметров и различного числа уровней варьирования по каждой n-мерной координате,

- число зон устойчивости либо неустойчивости движения управляемых колес машины(к₁) при одновременном варьировании значений сначала одного параметра (к₁=1), затем двух (к₁=2),…,(n-1), при этом к₁=n-1 значений n параметров (к₁=n) из совокупности, содержащей n параметров, при неизменных значениях остальных значений в этой совокупности параметров.

Формулы и (к₁) будем выводить для двух случаев, когда число уровня варьирования по каждой n-мерной координате различно - ,,…, (где i, j,…, N- текущие порядковые номера уровней варьирования по каждой n-мерной координате i=; j=; … ; N=, соответствуют количеству порядковых номеров уровней варьирования) и когда это число одинаково ==…==λ и ==…==f. В последнем случае формулы и (к₁) приобретают вид: и (к₁).

Чтобы установить вид формулы , рассмотрим рисунок 1.1, на котором изображена плоскость (n=2) и пространство (n=3) совершенно различных по физическому смыслу параметров с отличным друг от друга числом уровней варьирования по каждой из трех координат:

,,, где i=; j=; … ; k=.

Тогда =4,=2,=3.

Легко определить,что количество совокупностей параметров на плоскости (рисунок 1.1,а) и в пространстве (рисунок 1.1,б) соответственно равно:

=*; =**;

=4*3=12; =4**3=24.

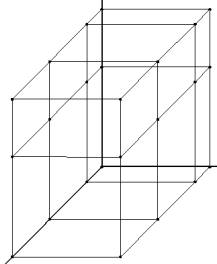
а) б)

Рисунок 1.1

В n-мерном пространстве параметров количество их совокупностей, содержащих по n параметров каждая, определяется следующей зависимостью:

1.3

Здесь необходимо обратить внимание на следующее обстоятельство. В отличие от произведения * * *…*, которое определяет значение , запись вида (1.3) является названием всего лишь одной из совокупностей параметров в n-мерном пространстве (смотри рисунок 1.1).

Вывод формулы (к₁) при к= будем осуществлять исходя из предположения, что скорость движения управляемых колес является функцией совокупности параметров V=V(,,…,), которая представляет поверхность в n-мерном пространстве.

Рассмотрим вариант, где скорость движения колес является функцией двух параметров V=V(;). Чтобы изучить эту поверхность в случае варьирования величины одного из них при неизменном значении второго необходимо выполнить следующее:

А) Варьировать величину одного из параметров, например , при неизменной какой-либо одной из величин , например =const. При этом получим ряд точек =(где i=), через которые, используя методы оптимизации, можно провести плавную кривую. Зависимость =(,) и представляет собой одну плоскую зону устойчивости и неустойчивости (рисунок 1.2,б). Подобных зон устойчивости вида =(,) нужно построить j=.

Б) Помимо этих зон необходимо построить еще и число j= зон устойчивости вида =(,), где j= (рисунок 1.2,в). Здесь варьируется величина при уже неизменной величине =(где i=).

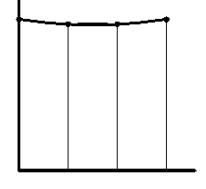
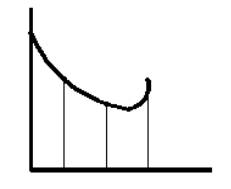
б) в)

Рисунок 1.2

Очевидно, что полное количество плоских зон устойчивости соответствует числу горизонтальных и вертикальных прямых, проведенных через соответствующие совокупности параметров на плоскости двух параметров. Например, согласно рисунку 1.1(а) количество горизонтальных линий равно трем, а количество вертикальных равно четырем. Следовательно, для изучения поверхности V(,) необходимо построить семь плоских зон устойчивости. А для изучения, например, поверхности V(,), изображенной на рисунке 1.2(а), необходимо построить восемь плоских зон устойчивости.

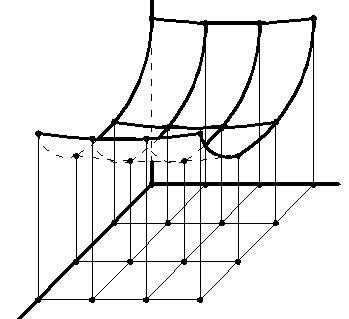
а)

рисунок1.2

Таким образом, для изучения поверхности V(,) по методике, где варьируют значения одного параметра при неизменных значениях второго, необходимо построить следующее количество плоских зон устойчивости:

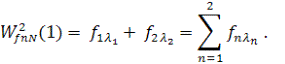
Если одновременно варьировать величины двух параметров, то для изучения поверхности V(,) необходимо построить всего одну область устойчивости, изображенную на рисунке 1.3(а).

Таким образом, оказалось, что при одновременном варьировании n параметров необходимо строить всего лишь одну n-мерную картину устойчивости.

Это позволяет из имеющегося большого количества методов нелинейного программирования выбрать методы случайного поиска.

В результате нами выбран метод Монте-Карло, который относится к случайному поиску. Необходимо подчеркнуть основное достоинство метода Монте-Карло, заключающееся в его независимости от условий задачи. С помощью генератора псевдослучайных чисел вырабатываются точки, которыми просматривается многомерное пространство варьируемых параметров.