Е.В.Липай, П.Н.Самусев, Ю.А.Гурвич

Белорусский национальный технический университет

Динамика вращающихся систем с учетом сил упругости

Вал любого роторного агрегата является его важнейшей составной частью, поскольку производительность, точность технологических операций, ресурс агрегата и другие важные показатели зависят, прежде всего, от динамических перемещений и напряжений в материале вала. K валу непосредственно примыкают многие узлы и детали ротора и статора, надежность и экономичность которых в первую очередь зависят от работоспособности и размеров вала.

B зависимости от количества установленных на валу дисков, шкивов, барабанов, мешалок, зубчатых колес, муфт и других узлов и деталей разнообразного назначения различают валы с одной и многими сосредоточенными массами. При этом относительно менее массивные элементы полагают лишенными массы. Пο виду поперечного сечения валы различают постоянного и переменного сечений. В зависимости от места установки подшипников валы подразделяют на однопролетные (с концевой опорой) и консольные.

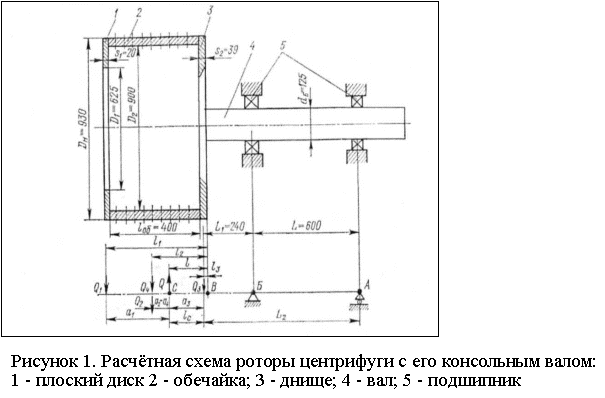
Ha рисунке 1 представлена расчётная схема роторы центрифуги с его консольным валом.

В расчёте не учитывается собственный вес вала и его переменное сечение принято постоянным с диаметром d=0.125 мм. Размеры барабана и вала показаны на рисунке 1. Материал вала и барабана сталь с характеристиками:

- модуль упругости E=2*10¹¹Па;

- плотность p=7800 кг/м³ ;

- коэффициент Пуассона μ=0,3.

Проверим выполнения условия виброустойчивости ротора центрифуги оценки влияния на критическую скорость (ω_κρ) вылета его центра массы относительно центра ступицы днища барабана используем методику изложенную в [1].

Определение масс:

- Масса плоского кольцевого диска т₁ = π(D_n²–D₁²)s₁p/4=58кг ;

- Масса цилиндрической обечайки т₂ = π(D_n² –D₂²)1_o6p/4 = 134.5κг;

- Масса диска (днища) барабана m₁ = π D_n²s₂ p/4 = 206.5кг ;

- Общая масса ротора m = ∑m_i= 400кг.

Сила тяжести: Q₁ = m_ig, Q = mg;

Расстояния от центра масс деталей до точки B (рисунок 1):

Расстояние от центра массы барабана до края днища из условия равенства нулю суммы моментов относительно точки В

Расстояние от центра массы барабана до центров масс деталей:

Вылет центра массы барабана

Моменты инерции вращающихся масс:

Осевые:

Окружные:

Моменты инерции всего барабана:

;

;

Критическая скорость вала при условии, что вся масса барабана сосредоточена в точке Bего крепления к валу:

Критическая скорость вала при учёте вылета центра массы барабана от точки B крепления его на валу и с учётом массы барабана

(

B ряде важных практических случаев данные формулы дают лишь первое грубое приближение.При расчёте ω_κρ, во избежание опасных резонансных явленийпри работе ротора необходимо его конструировать в соответствии с более точными формулами или методами расчёта, отражающими влияние на ω_κρтаких факторов,как вылет центра массы барабана относительно точки его крепления на валу, упругость опорных подшипников, собственная масса вала, изменение его поперечного сечения.

Как видно по результатам расчёта, пренебрежение одним или несколькими параметрами, при создании расчётной модели, ведёт к значительной погрешности расчётов. Поскольку представленный метод не позволяет учесть собственную массу вала, собственные частоты самого барабана, податливость опор и внешние воздействия на систему (усилия от натяжения ремней, дисбалансы ротора и т.д.) возникает необходимость применения более совершенных методов расчёта (численные методы).