Бурак О. Ю., Ярохович А.И., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Решение задач синтеза кинематики и динамики сложного движения точки

В качестве критерия в задачах синтеза кинематики сложного движения точки используется одно из значений абсолютного ускорения точки , причем , а содержит все пять слагаемых ().

Примеры задач синтеза. Дано: критерий - одно из 24-х значений .

Требуется определить: r, e, или , n, m, a, b, g, y, x, q и сформировать схему сложного движения точки

где: r - относительное движение точки (прямолинейное или криволинейное); e - переносное движение (поступательное прямолинейное, поступательное криволинейное или вращательное);

или - законы относительного, переносного (поступательного или вращательного) движений;

n, m - целые числа; - постоянные положительные коэффициенты; ; ; ; ; ; ;

угол a может принимать одно из трех значений -””, “”, “ не существует”, ;

каждый из углов может принимать одно из трех значений - “=p/2”, “¹p/2” , “не существует”.

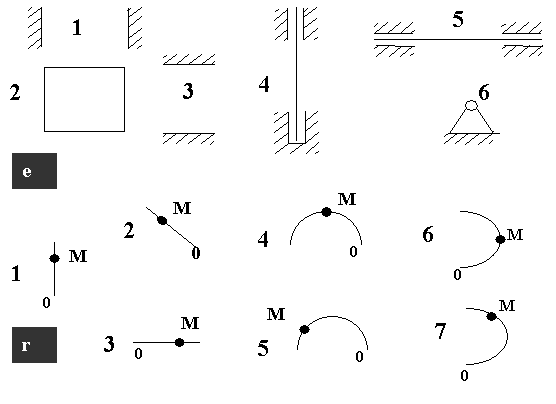
1. Укажите номера представленных в таблице характеристик относительного и переносного (е) движений и сформируйте из отдельных элементов схемы сложного движения точки М в соответствии с критериями - числом и видом слагаемых ее абсолютного ускорения . Покажите на схемах векторы слагаемых абсолютного ускорения точки и векторы , , .

1	прямолинейное	r	8	Se=B2t^m	e
2	криволинейное	r	9	jе=B3t^m	e
3	Sr=B1t^n	r	10	m=1	m
4	n=1	n	11	m=2	m
5	n=2	n	12	=kp, k=0,1	a
6	поступ. прямолин.	e	13	¹kp, k=0,1	a
7	вращательное	e	14	не существует	a

0251659264251660288251661312251662336251663360251665408251664384251666432251667456251668480251669504251670528251671552251673600251672576

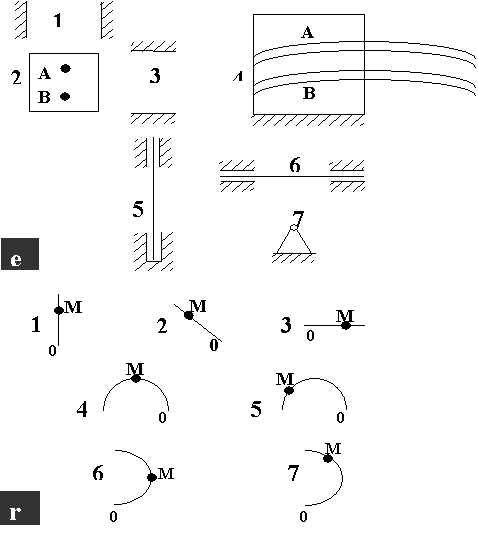
2. Покажите номера представленных в таблице характеристик относительного и переносного (е) движений и сформируйте из отдельных элементов схемы сложного движения точки М в соответствии с критериями - числом и видом слагаемых ее абсолютного ускорения . Покажите на схемах векторы слагаемых абсолютного ускорения точки и векторы , , .

1	прямолинейное	r	8	вращательное	e	15	не существует	a
2	криволинейное	r	9	Se=B2t^m	e	16		b
3	Sr=B1t^n	r	10	jе=B3t^m	e	17		b
4	n=1	n	11	m=1	m	18	не существует	b
5	n=2	n	12	m=2	m	19		g
6	поступ. прямолин.	e	13	=kp, k=0,1	a	20		g
7	поступ. криволин.	e	14	¹kp, k=0,1	a	21	не существует	g

0251659264251660288251661312251672576251662336251664384251665408251666432251667456251669504251668480251670528251671552251675648251674624

Задачам синтеза присуща многозначность решений. Например, критерию , будут соответствовать две схемы: с переносным поступательным криволинейным движением и с переносным вращательным движением, что дает дополнительные возможности конструктору для принятия окончательного решения.

В динамике автор реализует методику постановки и решения задач синтеза динамики относительного движения точки: «Сформировать схему движения материальной точки в неинерциальной системе отсчета с заранее заданными свойствами за счет изменения эйлеровых сил инерции».

В качестве критериев в задачах синтеза могут использоваться: одно из восьми значений абсолютного ускорения , , причем , ,¼, ; или - минимальное или максимальное давление, например, шарика на стенки канала (см. Д-4 из сборника заданий для курсовых работ по теоретической механике под редакцией А.А.Яблонского, где автор изменяет условия задач с целью научить студентов реализовывать идеи синтеза на практике).

Пример задачи синтеза. Дано: критерий - одно из 8-ми значений или критерии - одно из 8-ми значений и или N_max. Требуется определить: или и сформировать схему движения материальной точки в неинерциальной системе отсчета.

Решая одну из задач синтеза, студент практически осуществляет постановку всех задач анализа соответствующих заданному критерию. Уже одно это обстоятельство резко повышает уровень знаний студента.

Применение в учебном процессе новой методики многокритериального синтеза способствует формированию современного мышления студента, повышает эффективность обучения. Приобретенные навыки помогут будущему специалисту успешно решать задачи проектирования механизмов с заранее заданными свойствами, принимать наилучшее из всех возможных решений.