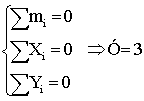Бурак О. Ю., Ярохович А.И., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Анализ возможностей критерия СТ

В статике существует несколько способов решения задачи, но необходимо найти рациональное решение, которое позволит быстрее достичь желаемого результата.

Рациональное решение задач статики с помощью критерий СТ

Введём понятие критерия СТ – степень статической определимости-неопределимости.


 где: СТ – целые числа; Н – суммарное количество неизвестных составляющих реакции опор и шарниров составной конструкции; У – количество линейно независимых уравнений равновесия, присущих каждой из шести систем сил; i – количество тел, входящих в составную конструкцию.

Если СТ = 0, то необходимо указать работоспособна данная конструкция или нет.

Методика рационального решения задач статики составных конструкций с применением критерия СТ

Для выбора рационального решения задач статики составных конструкций необходимо:

1. Определить СТ составной конструкции в целом:

1.1 Если СТ > 0, то такая конструкция статически неопределима, задача не решается методами статики;

1.2 Если СТ < О, то такая конструкция статически неопределима, задача не решается методами статики

1.3 Если СТ = 0, то такая система статически определима, задача имеет решение.

2. Разделить конструкцию по шарнирам на составные части и определить СТ каждой части в отдельности.

При этом могут иметь место следующие варианты:

– по крайней мере у одной из нескольких частей конструкции СТ = 0. В данном случае решение задачи следует начинать с рассмотрения равновесия этой части. А затем, используя формулы перехода от одной части к другой (, ), приложить определенные ранее составляющие реакций шарнира к следующей части, что сделает ее статически определимой (с СТ = 0);

– если СТ всех частей не равны 0, то решение задачи следует начать с рассмотрения равновесия всей конструкции в целом, и определить составляющие реакций приложенных к ее частям. Это сделает обе части конструкции статически определимыми. Далее следует рассмотреть равновесие более простой части.

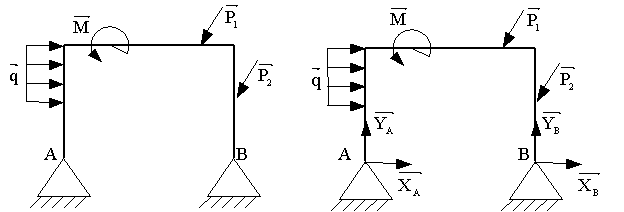Продемонстрируем возможности критерия СТ на примере бес шарнирной конструкции (рис. 1).

Рис.1

Определим критерий СТ конструкции по формуле (1):

1. Число составных частей конструкции (i) равно единице.

2. Число неизвестных составляющих реакции конструкции Н равно четырём (, , , ).

3. Определим число линейно независимых уравнений равновесия конструкции У.

Так как реакции и внешние силы образуют плоскую произвольную систему сил, то для её равновесия необходимо, чтобы главный вектор R* и главный момент  системы сил, были равны нулю.

Отсюда вытекают три скалярных равенства:

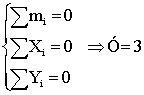
Подставив значения в формулу (1), получим:

СТ = 4 – 3 = 1.

Следовательно, конструкция статически неопределима.

Рассмотрим раз­личные варианты преобразования конструкции, позволяющие привести эту систему к статически определимой.

Проведём в системе некоторые изменения, чтобы СТ  равнялось нулю.

Для этого нам необходимо либо уменьшить количество неизвестных Н (изменяя виды опор), либо увеличить число линейно независимых уравнений У (вводя в конструкцию шарнир).

Вариант А.

Например введём в систему шарнир.

Например введем в систему шарнир С.

Проверим статическую определимость системы с помощью критерия СТ.

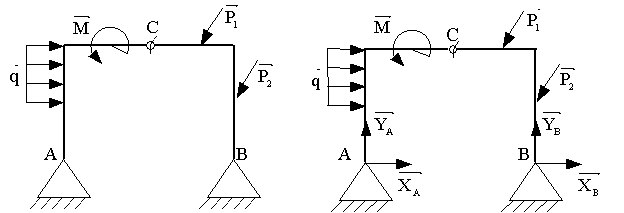
Мысленно расчленим полученную конструкцию (рис. 2) (составляющие реакции  ,  не показаны) по шарниру и определим критерий СТ:

Рис.2
 
i = 2;    H = (, , , , , ) = 6;

 

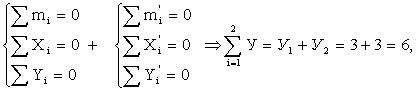
СТ = 6 – 6 = 0.

Следовательно, с введением в систему шарнира, конструкция стала статически определимой.

Вариант В.

Заменим неподвижную опору В подвижной, уменьшив тем самым число неизвестных реакций на единицу (рис. 3).

Определим критерий СТ полученной конструкции:

i =1;

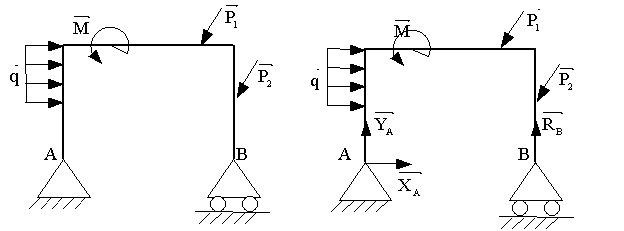Н = (, , ) = 3;

СТ = 3 – 3 = 0.

Следовательно, уменьшение числа неизвестных реакций, за счет за­мены одного вида связи другим, позволяет сделать конструкцию статиче­ски определимой.