Лаптанович Д.М ., Путят В.А., Друтько К.И., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Постановка задачи оптимизации параметров пар скольжения методом сеток

К ползуну пресса в форме параллелепипеда весом P и шириной b через невесомую консоль приложена сила Q, которую можно перемещать по консоли. Коэффициент трения между ползуном и направляющими f (все остальные размеры на рисунке 1).

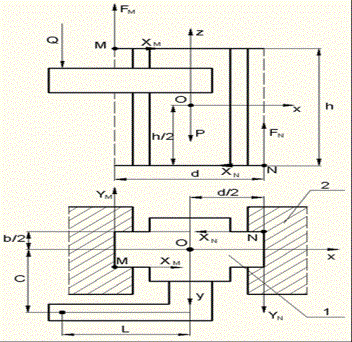
Рисунок 1 − Ползун пресса в направляющих:

1 – ползун, 2 – направляющие.

Основным критерием оптимизации конструктивных параметров ползуна пресса является величина запаса гарантированного скольжения. Данная величина измеряется в процентах и численно показывает часть зоны гарантированного скольжения, находящейся между точкой приложения силы Q к пуансону и границей гарантированного скольжения, по отношению к значению всей зоны гарантированного скольжения.

Таким образом, требуется произвести оптимизацию исходных параметров b, d, h, f, P/Q по критериям W1, W2, W3, W4.

Согласно литературе известно четыре критерия оптимизации ползуна пресса, которые позволяют исключить механические колебания:

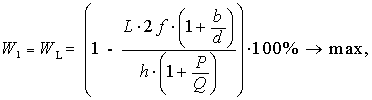
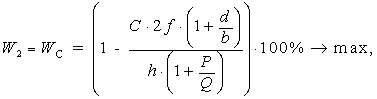
Существуют методика оптимизации конструктивных параметров пары скольжения «ползун-направляющая» по критериям гарантированного скольжения одного тела по другому. Оптимизация параметров в методике осуществлена с использованием метода сеток.

Рассмотрим суть данного метода на примере оптимизации параметров по критерию представляющему собой функцию двух некоторых переменных А и В. Пусть значения каждого оптимизируемого параметра изменяются в некотором допустимом интервале. Разобьем этот интервал изменения значений параметров на 9 подинтервалов, что будет соответствовать 10 расчётным точкам (узлам) и некоторому шагу изменения величины параметра: h. Значения критерия будем рассчитывать, оставляя значение параметра А неизменным и при этом варьируя десятью значениями параметра В. Рассчитав 10 возможных значений критерия К, изменяем значение параметра А на соответствующий шаг и, варьируя значениями параметра В, снова рассчитываем 10 значений критерия К. Так продолжаем до тех пор, пока не просчитаем всевозможные комбинации значений оптимизируемых параметров (рисунок 2).

Очевидно, что, так как оптимизируемых параметров 2 и изменяются они в пределах 10 значений, то всего получится 100 вычисленных значений критерия.

Общая формула для количества вычисленных значений критерия для метода сеток:

где N – количество рассчитанных значений критерия, n – число варьируемых значений параметра (в данном примере n = 10), m – количество оптимизируемых параметров системы.

Метод сеток не позволяет гарантировано определить оптимальные значения и построить область Парето-решений. При использовании метода сеток для n-мерного пространства параметров требуется большое количество итераций, что существенно увеличивает время на оптимизацию и разработку ползуна пресса.

Задача оптимизации конструктивных параметров пресса с возможностью гарантированного определения оптимальных значений , построения области Парето-решений и снижения времени расчета является актуальной.

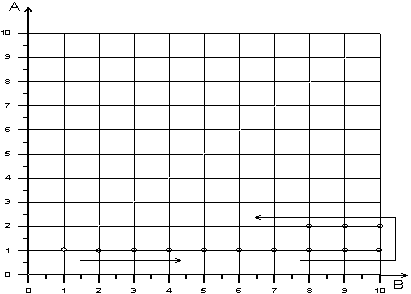
Рисунок 2 – Алгоритм реализации метода сеток

Так как критерии WL и WC представляют собой величины запасов гарантированного скольжения, то оптимальными значениями конструктивных параметров ползуна будут являться те, при которых значения величин запасов скольжения будут максимальными. Эти значения наиболее точно получаются при выборе методом сеток.