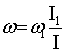Лысанович П.В., Ярохович А.И., Гурвич Ю.А.
Белорусский
Национальный Технический Университет
Закономерности
вращения фигуриста при вязком трении между коньком и льдом
|
Рис.1 |
Определим угловую
скорость вращения фигуриста относительно оси Z (рис.1) в функции времени |
Используя теорему об
изменении кинетического момента фигуриста относительно оси Z, получим ![]() , где
, где ![]() - момент инерции
фигуриста относительно оси Z в функции времени
- момент инерции
фигуриста относительно оси Z в функции времени ![]() . Решая это дифференциальное уравнение с разделяющимися
переменными, получим:
. Решая это дифференциальное уравнение с разделяющимися
переменными, получим:
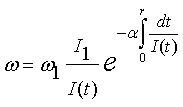 . (1)
. (1)
Зададим вид функции ![]() . Предварительно примем, что: время вращения фигуриста равно
сумме времени разгона и торможения
. Предварительно примем, что: время вращения фигуриста равно
сумме времени разгона и торможения ![]() ;
;
![]() изменяется по линейному закону:
изменяется по линейному закону:
![]() , где
, где 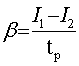 . (2)
. (2)
Тогда ![]() .
.
Теперь решение (1) с учетом (2)
имеет вид:
![]() . (3)
. (3)
Рассмотрим 3 случая: ![]() и построим графики
для (3).
и построим графики
для (3).
1.
Если ![]() (рис.2), тогда (3) примет вид:
(рис.2), тогда (3) примет вид:
 ,
, 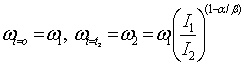 . (4)
. (4)
Функция (4) определена и
возрастает на интервале времени 0 < t < tp, а кривая (4) имеет
вертикальную асимптоту t=![]() . Определим
производную по времени от (3) для выявления характера построения графиков:
. Определим
производную по времени от (3) для выявления характера построения графиков:
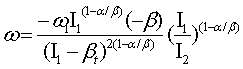 . (5)
. (5)
Так как
производная (5) положительная величина и возрастает на интервале 0< t < tp, то кривая (3) -
вогнутая на этом интервале времени.
2.При ![]() =1 кривая (3) примет вид:
=1 кривая (3) примет вид:
![]() const (6)
const (6)
при любом t> взятом из интервала
времени 0![]() t
t![]() tp.
tp.
3. Если ![]() >1, тогда (3) примет вид:
>1, тогда (3) примет вид:
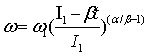 .
(7)
.
(7)
Функция (7) определена и
убывает на интервале времени 0![]() t
t![]() tp. Определим первую производную по времени от функции (7):
tp. Определим первую производную по времени от функции (7):
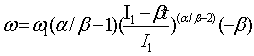 . (8)
. (8)
В связи с
видом функции (8) целесообразно рассмотреть еще три случая.
3.1.Если
1< α/β < 2» то производная (8) примет вид:
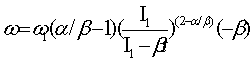 . (9)
. (9)
Производная
(9) - отрицательная величина и убывает на интервале времени 0![]() t
t![]() tp. Следовательно, кривая (7) в этом
случае - выпуклая и убывает на этом интервале времени.
tp. Следовательно, кривая (7) в этом
случае - выпуклая и убывает на этом интервале времени.
3.2. При α / β = 2 производная (8) - отрицательная и постоянная величина. Следовательно,
графиком функции (7) является отрезок
прямой на интервале
0![]() t
t![]() tp.
tp.
3.3 При α/ β > 2 производная (8) на интервале времени 0![]() t
t![]() tp - отрицательная величина и возрастает. Следовательно, график (7) убывает и имеет вогнутость
на этом интервале времени.
tp - отрицательная величина и возрастает. Следовательно, график (7) убывает и имеет вогнутость
на этом интервале времени.
Интересно
знать, что будет с ω(t) при ![]() и t>tp? Дифференциальное уравнение вращения фигуриста в этом случае имеет вид:
и t>tp? Дифференциальное уравнение вращения фигуриста в этом случае имеет вид:
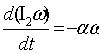 . (10)
. (10)
Решая (10),
получим 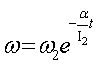 .
.
Необходимо
установить вид зависимости ω=ω(t) в тривиальном случае, когда фигурист из положения с I1 переходит в положение I2 (при этом Мс=0).
Для
этого случая имеем:
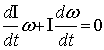 . (11)
. (11)
Решая (11) получим:
Если в (12) подставить I=I(t)=I1 -βt, то получим:
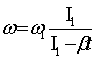 . (13)
. (13)
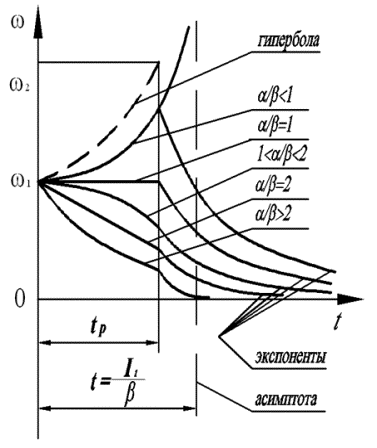
Рис.1
Графиком функции (13) является гипербола на интервале времени 0![]() t
t![]() tp (штриховая
линия). Сравнивая графики (4) и
(13), приходим к выводу о большем
значении ординаты (13) по сравнению с ординатой (4).
tp (штриховая
линия). Сравнивая графики (4) и
(13), приходим к выводу о большем
значении ординаты (13) по сравнению с ординатой (4).