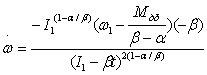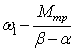Лысанович П.В., Ярохович А.И., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Закономерности вращения фигуриста при одновременном действии вязкого и сухого трения между его коньком и льдом 

В случае одновременного действия вязкого и сухого трения дифференциальное уравнение имеет вид:

,                                                            (1)

где Ι=Ι1 -βt ,тогда

    .                                            (2)

Уравнения (1) и (2) имеют решение:

ω = ω* +ω**,                                                                                 (3)

 где ω* - частное решение уравне­ния (2); ω** - общее решение однородного уравнения, которое, как известно из (1), имеет вид:

ω**=;                                                      (4) 

С - произвольная постоянная.

Частное решение будем искать в виде ω* = const.  Тогда ω*   = 0. Подставим ω*  и ώ*    в (2), получим:

ω* 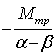 = .                                                             (5)

Найдем С, используя (3) и (4) при начальных условиях ω t=0 = ω1 . Тогда             С = ω1+.

Общее решение уравнения (1) получает вид:

 ω =I1(1-α/β)(I1 -βt)(α/ β-1)( ω1+)* ()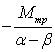.                                     (7)

Отметим, что решение (7) справедливо только для случаев α/β<1 и α / β > 1.

 Рассмотрим случай, когда α = β, тогда (2) принимает вид:

 (I1 -βt) = -Mтр.                                                                        (8)

Отсюда

ω = ω1+*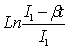.                                                                 (9) 
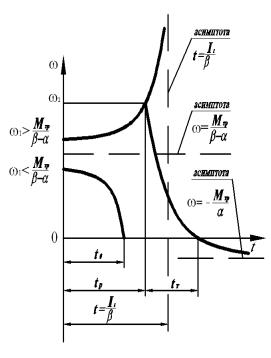
Построим график функций (7) и (9) соответственно для случаев    α/β<1,α/β>1 и α = β. Если α /β < 1 (рис. 1), тогда (7) примет вид:

ω = 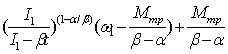.                                                   (10)

ωt=0=ω1 ωt=tp=ω2=(I1/I2)(1-α/β)×.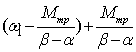

Функция (10) определена на интервале времени   0 ≤ t≤  tp , а кривая   ω = ω(t) имеет две асимптоты: горизонтальную ω =и  вертикальную t= I1/β.

Рис.1

Если ω1 >, функция (10) возрастает, в противном случае - убывает. Определим   ώ, для решения вопроса о характере графика функции (10).

.                     (11)

Если  ()> 0, то ώ возрастает, тогда кривая (10) – вогнутая, если - наоборот, то кривая (10) - выпуклая.

Определим , когда ,

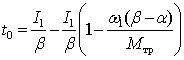.                                                    (12)

Интересно знать, что будет с  при  для случая 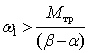 (наиболее интересный и важный для зрителей и судей случай)? При этом  имеет вид:

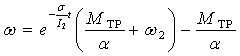
       .                                (13)

Кривая (13) имеет горизонтальную асимптоту .

Определим время торможения   при .  При этом

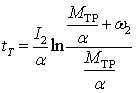.                                                       (14)

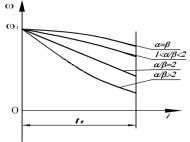
Рассмотрим случай    (рис.2). Тогда (7) приобретает вид:

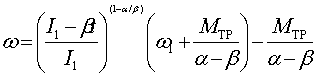.                              (15)

Функция (15) определена на интервале времени . Производная  на интервале -отрицательная и убывает, поэтому график (15)-выпуклый и убывает. Если , то  на интервале -отрицательна и возрастает.

Поэтому кривая (15) на этом интервале имеет вогнутость и убывает.

При    (рис. 2) график (15) –прямая линия (об этом также говорит значение ).

В случае (рис.2) производная по времени от (9) имеет вид  и на интервале -отрицательно убывает. Поэтому график функции (9) убывает и является выпуклым.