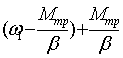Лысанович П.В., Ярохович А.И., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Закономерности вращения фигуриста при действии сухого трения между его коньком и льдом        

Используя теорему об изменении кинетического момента фигуриста относительно оси Ζ, получим:

 d(Iω)/dt = --Mтр                                                                                                                           (1).  

 Разделим переменные в (1) и от обеих частей возьмем определенные интегралы с переменными верхними пределами:      

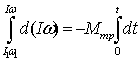  .                                                                 (2)  

Окончательно из (2) получим ω (t):

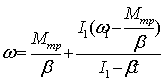  ,                                                      (3)

ωt=0=ω1 ωt=tp=ω2=I1/I2

Функция (3) определена на интервале 0≤t ≤ t p (рис.1), а кривая  ω = ω(t) имеет две асимптоты: горизонтальную ω = при 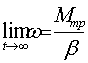       и вертикальную t=I1/β при I1-βt= 0. Если ω1>- функция (3) возрастает, в противном случае – убывает. Определим первую производную по времени от функции (3) для выяснения характера протекания функции на интервале 0 ≤ t ≤tp

ώ=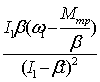

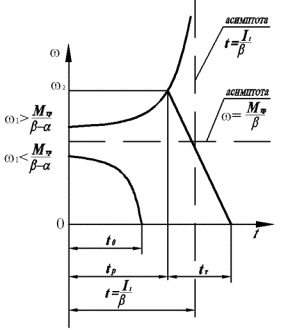
Рис.1

Если ω1>, то ώ  положительная величина и возрастает, тогда кривая (3) - вогнутая. При ω1< производная (4) - отрицательная величина и уменьшается, что соответствует выпуклости кривой (3) на интервале времени 0 ≤ t ≤t p.

Определим t0 , когда ω = 0 при ω1<- t0=I1ω1/Mтр.

Необходимо ответить на вопрос, что будет с ω при I=I2=const и t>tp для случая ω1>?  

Из(2)следует 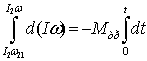 Определим ω(t)

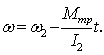                                                                            (5)

График функции (5) - отрезок прямой линии на интервале tp ≤ t ≤  t T , где время торможения t T= I2ω2/Mтр.