Корзун А.С., Крайник Д.А., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Реализация на ЭВМ перемещения твёрдого тела брошенного под углом к горизонту с учётом сил сопротивления

 

Перед нами ставиться цель, решить задачу о движении артиллерийского снаряда с учетом сопротивления воздуха пропорционального второй степени скорости движения численным способом, с помощью метода Рунге-Кутта 4-го порядка.

В работе приводятся результаты теоретических исследований падения тяжелого тела в воздухе при квадратичном законе сопротивления. Получен ряд аналитических зависимостей, характеризующих основные параметры этого движения. Новизна работы заключается в том, что впервые данная задача была решена численным методом на ЭВМ с помощью метода Рунге-Кутта 4-го порядка.

При полёте в воздухе подвергается действию двух сил: силы тяжести , и силы сопротивления . В результате действия этих сил скорость полёта снаряда постепенно уменьшается, а его траектория представляет собой по форме неравномерно изогнутую плавную кривую линию.

  Определение уравнений движения снаряда. Рассмотрим движение снаряда весом Р, которому сообщена начальная скорость  под углом α к горизонту, с учётом силы сопротивления   (рис. 1)

C:\Users\Demon\Pictures\Безимени-2.jpg   Рисунок 1

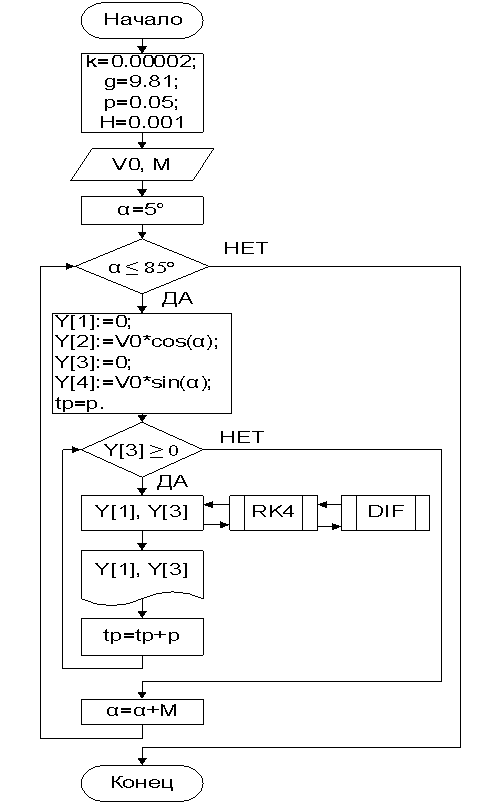
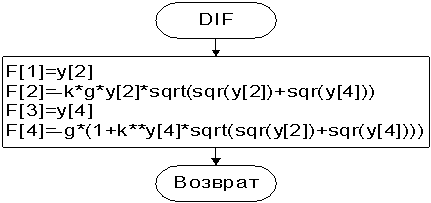
Блок схема алгоритма вычисления системы уравнений

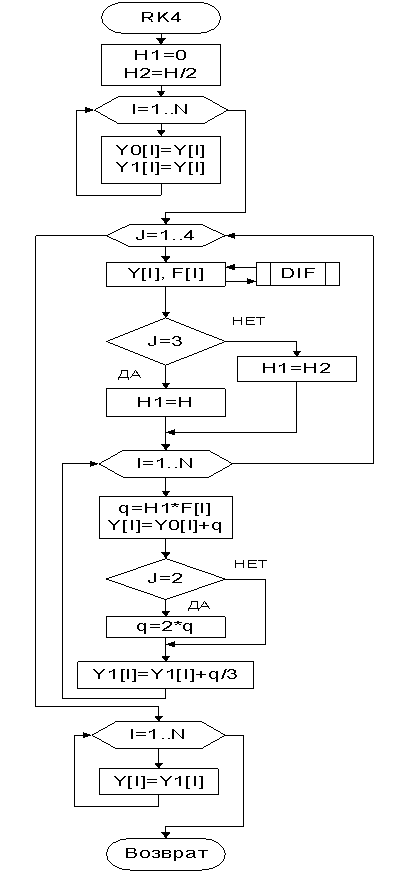
На рисунке 2 показана головная программа, на рисунке 3 показана процедура по вычислению методом Рунге-Кутта 4-го порядка.

 

Рисунок 2

Рисунок 3


Рисунок 4

А на рисунке 4 показана процедура, в которую подставлена решаемая система уравнений.

Данную систему уравнений нужно подставить  в процедуру DIF (рис. 4).

 

Вывод:

Была разработана блок схема для вычисления системы уравнений  различных программных продуктах Borland Delphi 7 в интегрированной среде Turbo Pascal 7.0, предназначенный для вычисления характеристик полета снаряда в безвоздушном пространстве и с учетом сопротивления воздуха.

Так же был определён угол при котором дальность полёта снаряда будет максимальной. Впервые данная задача была решена численным методом на ЭВМ с помощью метода Рунге-Кутта 4-го порядка.