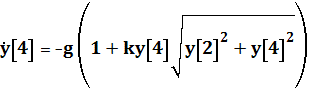Корзун А.С.,
Крайник Д.А., Гурвич Ю.А.
Белорусский
Национальный Технический Университет
Анализ движения артиллерийского
снаряда на ЭВМ по настильной траектории при сопротивлении воздуха
Данная задача относится к задачам внешней
баллистики – науки, изучающей движение снаряда после его вылета из ствола
орудия.
Для простоты модели артиллерийский снаряд будем
рассматривать как материальную точку, брошенную под углом 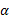 к горизонту с
начальной скоростью
к горизонту с
начальной скоростью 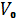 .
Рассмотрим
движение снаряда весом Р, которому сообщена начальная скорость
.
Рассмотрим
движение снаряда весом Р, которому сообщена начальная скорость 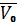 под углом α к
горизонту, с учётом силы сопротивления (рис. 1).
под углом α к
горизонту, с учётом силы сопротивления (рис. 1).
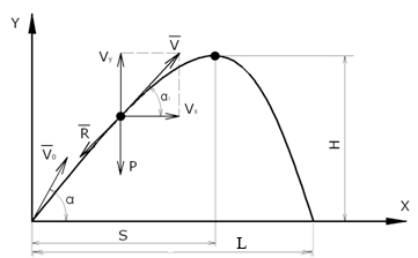
Рисунок 1.
Решим поставленную задачу о движении артиллерийского
снаряда при сопротивлении воздуха пропорционального второй степени скорости
движения на ЭВМ. Для этого воспользуемся методом Рунге-Кутта четвертого порядка, а программой реализации
– Turbo Pascal 7.0.
Заменим в уравнениях (1) и (2) 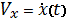 и
и 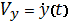 и получим:
и получим:
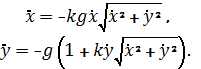

Для того
чтобы в программу подставить полученные уравнения (1) и (2) необходимо сначала
их преобразовать, сделав из двух уравнений второго порядка четыре уравнения
первого порядка.
Преобразовав,
получим четыре уравнения первого порядка
(3):
Но для решения на ЭВМ необходимо совсем избавиться от
степени, для этого создадим таблицу (таблица 1), в которой произведем все
нужные замены для программы, после которых программа сможет решить систему
уравнений (1) и (2).
Таблица 1
|
Массив производных
|
Массив функции
|
|
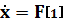
|
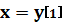
|
|
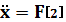
|
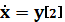
|
|

|
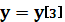
|
|
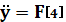
|
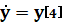
|
Преобразуем уравнения
(1) и (2) для программы используя таблицу 1, полученную систему уравнений
подставим в процедуру DIF.
Получим окончательную
преобразованную систему формул (4):
Проанализировав системы
уравнений (3) и (4), можно заметить, что изменилась только левая часть
уравнения. То есть, для более простого и быстрого преобразования можно было
заменить только левые части уравнений. Примем коэффициент сопротивления воздуха
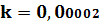 .
.
Программа реализация в интегрированной среде
Turbo Pascal 7.0
Program DU;
uses crt;
const
k=0.00002;
g=9.81;
p=0.05;
ci=0.001;
type mas=array[1..15] of real;
var y,v:mas;
Var tn,tp,al0g,al0r,H,V0:real;
tt,ttt:text;
Procedure Fun(t:real;Var V:Mas);
begin
v[1]:=z[2];
v[2]:=-g*k*z[2]*sqrt (sqr(z[2])+sqr(z[4]));
v[3]:=z[4];
v[4]:=-g*(1+k*z[4]*sqrt (sqr(z[2])+sqr(z[4])));
end;
{$I RK4.pas}
begin
clrscr;
assign(tt,'x.txt');
assign(ttt,'y.txt');
rewrite(tt); rewrite(ttt);
al0g:=5;
write('V0='); readln(V0);
write('H='); readln(H);
while al0g<=85 do
begin
writeln;
writeln(al0g:3:0);
writeln;
writeln(tt);
writeln(tt,al0g:3:0);
writeln(tt);
writeln(ttt);
writeln(ttt,al0g:3:0);
writeln(ttt);
al0r:=(pi*al0g)/180;
z[1]:=0;
z[2]:=V0*cos(al0r);
z[3]:=0;
z[4]:=V0*sin(al0r);
tn:=0; tp:=p;
repeat
RK4(4,tn,tp,ci,y,v);
writeln(tp:10:3,' ',y[1]:10:3,' ',y[3]:10:3);
writeln(tt,y[1]:10:3);
writeln(ttt,y[3]:10:3);
tn:=tp; tp:=tp+p;
until(y[3]<=0);
al0g:=al0g+H;
end;
readln;
close(tt); close(ttt);
end.
Вывод:
Разработан
программных продукт в интегрированной среде Turbo Pascal
7.0, предназначенный для численного решения дифференциальных уравнений методом
Рунге-Кутта, что позволило определить точное время и дальность полета снаряда с
учетом сопротивления воздуха пропорционально второй степени скорости движения.
![]() к горизонту с
начальной скоростью
к горизонту с
начальной скоростью ![]() .
Рассмотрим
движение снаряда весом Р, которому сообщена начальная скорость
.
Рассмотрим
движение снаряда весом Р, которому сообщена начальная скорость ![]() под углом α к
горизонту, с учётом силы сопротивления (рис. 1).
под углом α к
горизонту, с учётом силы сопротивления (рис. 1).
![]() и
и ![]() и получим:
и получим: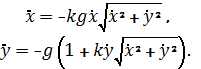
![]()