Корзун А.С., Крайник Д.А., Горбач Н.И., Гурвич Ю.А.

Белорусский национальный технический университет, Минск

Анализ некоторых характеристик движения твёрдого тела под углом к горизонту

Одними из основных характеристик движения твёрдого тела являются: определение времени t полета снаряда; определение дальности полета снаряда L; а так же мы рассмотрим определение двух различных углов, при которых снаряд попадет в одну точку.

Определение двух различных углов, при которых снаряд попадет в одну точку.

Определим значение таких двух углов, при которых снаряд попадает примерно в одну и ту же точку, с величиной попадания 10 метров. Для этого построим таблицу 5 только при одной скорости и разными углами от до с шагом . Подчеркнем, что при каждом значении угла от 6º до 85º время полета снаряда определялось по методике, описанной в предыдущем подразделе.

Таблица 1

α	L	α	L	α	L	α	L
6	9230,578	26	16104,94	46	13562,11	66	8113,71
7	10175,38	27	16097,65	47	13339,61	67	7798,484
8	11007,4	28	16072,2	48	13110,49	68	7480,273
9	11739,42	29	16031,23	49	12875,21	69	7159,278
10	12394,62	30	15974,92	50	12633,98	70	6835,576
11	12957,59	31	15904,78	51	12387,02	71	6509,308
12	13460,12	32	15809,95	52	12134,36	72	6180,659
13	13829,54	33	15725,24	53	11876,38	73	5849,757
14	14288,22	34	15616,67	54	11613,12	74	5516,687
15	14626,72	35	15496,92	55	11344,93	75	5181,584
16	14918,3	36	15366,51	56	11071,98	76	4844,616
17	15172,42	37	15225,49	57	10794,31	77	4505,529
18	15387,14	38	15074,78	58	10512,22	78	4165,524
19	15570,35	39	14914,8	59	10225,77	79	3823,657
20	15721,56	40	14745,58	60	9935,231	80	3480,429
21	15844,62	41	14567,88	61	9642,087	81	3135,941
22	15941,57	42	14382,03	62	9342,399	82	2790,321
23	15967,46	43	14188,07	63	9040,325	83	2443,715
24	16065,48	44	13986,61	64	8734,772	84	2096,23
25	16095,51	45	13777,95	65	8425,877	85	1747,994

Анализ таблицы 5 показал, что существует три пары двух углов, при которых снаряд попадает в одну и ту же точку, разную для каждой пары, при углах:

, а - траектории 1 и 6;

, а - траектории 2 и 5;

, а - траектории 3 и 4.

Построим траектории полета снаряда с учетом сопротивления воздуха, используя полученные углы (рис. 1).

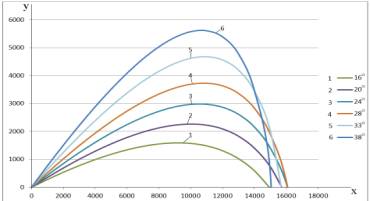
Рисунок 1

Определение времени t полета снаряда

Более точно определить дальность полета снаряда можно, зная время его движения по траектории. Для определения времени полета снаряда необходимо уравнение (2) решить графически, положив , а . В этом случае уравнение распадается на два уравнения:

Вычисления и приведены в таблице 2.

Таблица 2

, с	0	10	20	30	40	50	60	70
, м	0	2500	5000	7500	10000	12500	15000	17500
, м	0	5526,257	9260,372	11783,53	13488,44	14640,45	15418,87	15944,85

Определение дальности полета снаряда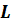

Для того чтобы определить дальность всего полета снаряда, необходимо подставить в уравнение (1) полученные данные и .

м.

Определение двух различных углов, при которых снаряд попадет в одну точку

Определим значение таких двух углов, при которых снаряд попадает примерно в одну и ту же точку, с величиной попадания 10 метров. Для этого построим таблицу 5 только при одной скорости и разными углами от до с шагом . Подчеркнем, что при каждом значении угла от 6º до 85º время полета снаряда определялось по методике, описанной в предыдущем подразделе.

Заключение

В работе учитывается четыре первых члена ряда Тейлора, что является грубым допущением и дальность полета снаряда, определенная по приближенному уравнению больше примерно на 12 000м дальности, вычисленной при тех же условиях по точному уравнению.

Оптимальный угол наклона ствола орудия при выстреле более точно определен в данной работе и отличается от α_опт, определенного в работе на 2,7^о в меньшую сторону, т.е. α_опт=31,5^о вместо α_опт=34,2^о.

Полученные данные, характеризующие движения снаряда, являются приблизительными, так как значение коэффициент сопротивления принято ориентировочно.