Бурак О. Ю., Ярохович А.И., Гурвич Ю.А.

Белорусский Национальный Технический Университет

Применение критерия СТ к решению задач статики

Критерий СТ

,

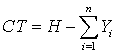где СТ – степень статической определимости неопределимости, которая измеряется действительными целыми числами; Н – число независимых составляющих реакций опор и шарниров составной конструкции; i – число элементов составной конструкции (количество тел, входящих в составную конструкцию); Y – количество линейно-независимых уравнений равновесия, присущих каждой из шести систем сил;

Для выбора рационального решения задач статики составных конструкций необходимо:

1. Определить СТ составной конструкции в целом:

1.1. Если СТ = 0, то такая система статически определима, задача имеет решение;

1.2. СТ > 0, то такая конструкция статически неопределима, задача не имеет решения;

1.3. СТ < 0, то такая конструкция неработоспособна, задача не имеет решения.

2. Разделить конструкцию по шарниру на составные части и определить СТ каждой части в отдельности.

При этом могут иметь место следующие варианты:

· только у одной из двух частей конструкции СТ = 0. В данном случае решение задачи следует начинать с рассмотрения равновесия этой части. А затем, используя формулы перехода от одной части к другой (), приложить определенные ранее составляющие реакций шарнира ко второй части, что сделает ее статически определимой (с СТ = 0);

· если СТ всех частей не равны 0, то решение задачи следует начинать с рассмотрения равновесия всей конструкции в целом, и определить вертикальные составляющие реакций приложенных к ее частям. Это сделает обе части конструкции статически определимыми. Далее следует рассмотреть равновесие более простой части.

С помощью новой методики рационального решения задач можно определить реакции опор:

1. составной балки 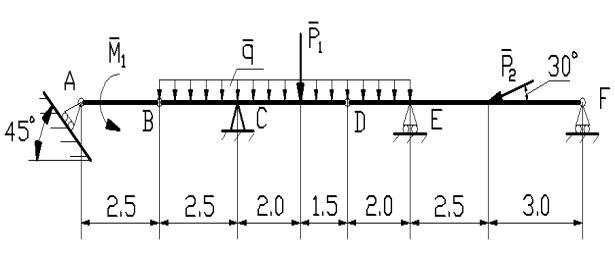(рис.1)

рис.1

Выбор рационального решения задачи (определение СТ конструкции)

СТ = Н – ∑Yi

СТ = 9 – (3+3+3) = 0

Часть конструкции
СТ конструкции	СТ1 = Н1 – ∑Yi1 СТ1 = 3 – 3 = 0	СТ2 = Н2 – ∑Yi2 СТ2 = 6 – 3 = 3	СТ3 = Н3 – ∑Yi3 СТ3 = 4 – 3 = 1

Отсюда делаем вывод схемы решения задачи: (1+(3+2)+3), т.е решаем сначала уравнения 1-й части составной балки, потом решаем совместно уравнения 3-й и 2-й части составной балки, а затем, совместно с предыдущими уравнениями, решаем уравнения 3-й части.

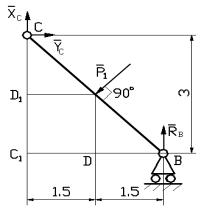
2. системы двух сил (рис.2)

Выбор рационального решения задачи (определение СТ конструкции)

СТ = Н – ∑Y_i

СТ = 6 – (3+3) = 0

Рис. 2

Часть конструкции
СТ конструкции	СТ1 = Н1 – ∑Yi СТ1 = 5 – 3 = 2	СТ2 = Н2 – ∑Yi СТ2 = 3 – 3 = 0

Отсюда делаем вывод схемы решения задачи: (2+1),т.е решаем уравнение 2-й части составной конструкции, а затем, используя полученные значения решаем уравнение 1-й части составной конструкции.

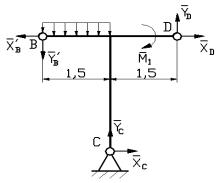
Системы трех сил (рис.3)

Выбор рационального решения задачи (определение СТ конструкции)

СТ = Н – ∑Y_i

СТ = 9 – (3 + 3 + 3) = 0

Рис.3

Часть конструкции
СТ конструкции	СТ1 = Н1 – ∑Yi СТ1 = 5 – 3 = 2	СТ2 = Н2 – ∑Yi СТ2 = 3 – 3 = 0	СТ3 = Н3 – ∑Yi3 СТ3 = 6 – 3 = 3

Отсюда делаем вывод схемы решения задачи: (3 + 1 + 2), т.е решаем уравнение 3-й части составной конструкции, а затем, используя полученные значения совместно решаем уравнения 1-й и 2-й частей составной конструкции.