Стульба М.А., Макаренко Р.Ю., Гурвич Ю.А.

Белорусский Национальный Технический Университет

ОЦЕНКА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПРИ РАЗЛИЧНОЙ ИНТЕНСИВНОСТИ ПОТОКА ФЛЮЕНСА НЕЙТРОНОВ

Упругое напряженно-деформированное состояние цилиндрических тел, находящихся под действием внутреннего давления, характеризуется тремя главными напряжениями у_r, у_и и у_z, имеющими различные значения и знаки. В целях упрощения рассматриваются два предельных случая: цилиндр бесконечно большой длины и цилиндр бесконечно малой длины. Первый случай составляет задачу плоских деформаций, а второй - плоских напряжений.

Постановка задачи В случае длинного цилиндра, температура в стенках которого изменяется по толщине и постоянна по длине, можно положить е_z=const. Влияние температуры и нейтронного облучения в этом случае учитывается добавлением к упругим деформациям деформаций вызванных температурным и нейтронным расширением тел. Тогда приращение полной деформации запишется в виде:

,

где e - полная деформация, e^e - упругая деформация, е^T - деформации, вызванные термическим расширением, e^s - деформации, вызванные радиационным распуханием.

Уравнения для случая плоских деформаций при осесимметричной постановке задачи, когда напряжения и деформации зависят от r, могут быть получены из уравнения равновесия и деформаций, где принимают е_г, е_и и е_z - деформации, а у_r, у_и и у_z - напряжения.

Вывод разрешающих уравнений

Воспользуемся соотношениями, представленными в работе, где были выведены выражения для определения радиальных, окружных и осевых напряжений, возникающих в телах сферической (7) и цилиндрической (8) геометрии от действия силовой и терморадиационной нагрузки:

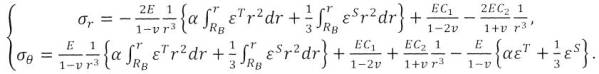
(7)

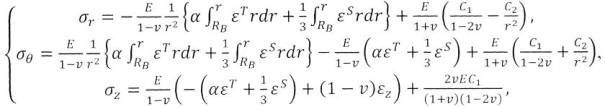
(8)

где E - модуль Юнга; ν - коэффициент Пуассона; ε^T - деформации, вызванные воздействием температуры; e^s - деформации, возникающие за счет действия потока нейтронов; r - текущий радиус; R_H и R_В - соответственно наружный и внутренний радиус; С₁ и С₂ - некоторые константы, значение которых определяется из граничных условий.

Учитывая, что элементы конструкций, подвергаемые воздействию силовой и терморадиационной нагрузки, зачастую имеют форму сплошной сферы (цилиндра) и полой, граничные условия принимают различный вид для топлива (9) и для оболочки (10):

(9)

(10)

где Р_н и Р_в - соответственно наружное и внутреннее давления.

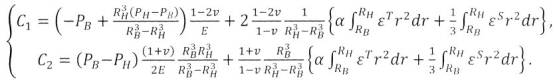Для первого случая константы С₁ и С₂ определяются из выражения (11) сферы, а для цилиндра - (12):

(11)

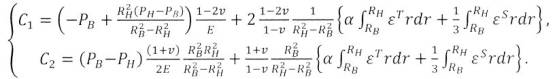
(12)

При определении констант для сплошного тела нижний предел интегралов можно считать равным нулю. Это означает, что константу С₂ можно принять равной нулю. Константа С₁ определяется выражением (13) для сферического тела, для цилиндрического - (14):

(13)

(14)

Рассмотрим более подробно случай полого цилиндра. С учетом граничных условий напряжения примут вид:

(15)

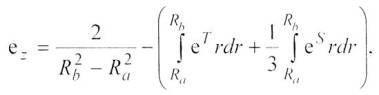
Для определения значения меридионального напряжения необходимо знать продольную деформацию е_z, которую находят, приравнивая нормальную силу к величине продольной нагрузки или к нулю, когда продольная сила отсутствует, т.е. в нашем случае: . Произведя интегрирование, получим:

(16)

после чего меридиональное напряжение будет определяться выражением:

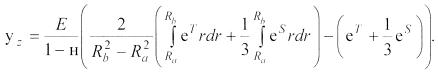
(17)

С учетом условий (17) перепишем выражение (15) в следующем виде:

(18)

Как видно из этого выражения каждое из главных напряжений представляет собой сумму отдельных напряжений возникающих от действия высокой температуры и облучением потоком флюенса нейтронов. С учетом сказанного, выражение (18) можно записать в сокращенной форме:

(19)

где - составляющие главных напряжений, вызванные соответственно силовым, тепловым и радиационным воздействием (i = r, и, z). Значения легко прослеживаются из выражения (18).