Распопов С.В. Николаенко Н.С. Гурвич Ю.А.

Белорусский национальный технический университет

Предпосылки формирования механико-математической модели поворота шарнирно-сочлененной машины с двумя осями

Исследований, посвященных изучению динамики поворота шарнирно-сочлененных колесных машин на стадии их проектирования. Данная работа посвящена исследованию маневренности подземного самосвала БелАЗ-75800 (Рис.1). В основу конструкции положен классический для подземных машин принцип компоновки: одноосный моторный модуль, шарнирно соединенный с грузовой задней частью.

Рис. 1. Габаритные размеры самосвала БелАЗ-75800

Объективным показателем процесса поворота являются траектории движения характерных точек машины. По виду траекторий можно судить об устойчивости движения машины на повороте, о вписываемости в заданный динамический коридор движения при различных управляющих воздействиях (угловая скорость складывания). При выводе дифференциальных уравнений движения самосвала сделаны следующие допущения:

- подвеска обоих мостов жесткая и центры тяжести секций располагаются в продольных вертикальных плоскостях симметрии;

- гироскопические моменты на колесах и силу сопротивления воздуха не учитывают.

В процессе неустановившегося поворота каждое из колес машины движется по криволинейной траектории переменного радиуса. Боковые силы, действующие на колесе каждого моста, суммируются и в виде P_δ1, Р_δ2 прикладываются к соответствующей оси (углы увода оси δ₁ и δ₂).

На рис. 2 представлена расчетная схема поворота машины с одним ведущим мостом, где точки О_i - мгновенные центры скоростей i–й секции (); A, D – середины центров осей колёс; B, C – центры тяжести секций машины; φ_i - углы курса i–й секции; θ – угол складывания; R_i – радиусы поворота i–й секции; P'_fi, P''_fi – силы сопротивления прямолинейному движению; Р_д1, Р_д2 – движущие силы на приводных колёсах.

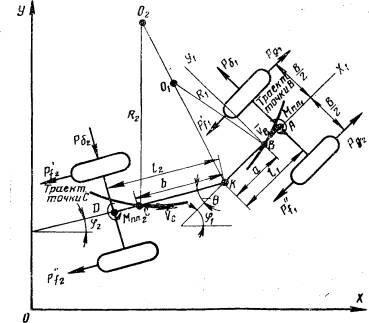
Рис. 2. Расчетная схема поворота шарнирно-сочлененной машины с одним ведущим мостом

Для вывода уравнений движения машины используем уравнения Лагранжа II рода.

где x_i – обобщенные координаты; Т – кинетическая энергия; Q_xi – обобщенные силы.

Положение шарнирно-сочлененной машины на плоскости определяется четырьмя обобщенными координатами: координаты центра масс передней секции Х_В и Y_B; угол курса передней секции φ1 и угол складывания (Рис. 3),где .

Рис. 3. Закон изменения угла складывания

Кинетическая энергия всей машины равна сумме кинетических энергий передней и задней секций

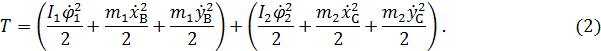
Кинетическая энергия машины в функции обобщённых координат имеет вид: