А.К.Танирбергенов - к.т.н., доцент (Алматы)

Элементы формализованного описания процесса принятия

решений и его интерпретация для задач транспортной системы

Как правило, решения вариантны, причем синтез решения и анализ его последствий (результатов) проходит под воздействием неопределенности, риска. Роль последнего усиливается двойственной природой системы, наличием сложных прямых и обратных связей с внешней средой.

В системном анализе сложилось базовое представление о сущности решения как выборе одного из некоторого множества рассматриваемых вариантов /1/: E_iÎE. Любой вариант E_i влечет за собой некоторый результат, допускающий количественную оценку e_i. По смыслу он может интерпретироваться как выигрыш, полезность (выигрыш - есть чистая полезность). Либо как мера достижения конкретной цели системы (надежность, экономичность, безопасность, экологичность и т.п.). В таких случаях цель анализа решений выбор оптимального варианта:

(1)

т.е. множество оптимальных вариантов E₀ состоит из тех вариантов E_i0, которые принадлежат полному множеству вариантов E и оценки которых e_i0

максимальны среди всех оценок e_i.

Однако вследствие открытости системы, двойственности ее природы каждому допустимому варианту решения E_i в зависимости от складывающихся независимо от лица, принимающего решение, внешних условий (состояний) F_j могут соответствовать различные последствия e_ij.

В задачах управления функционированием и развитием транспортной системы автору представляется наиболее существенным учет сценарных условий.

В частном случае, это может быть различная потребность в магистральном транспорте, исходя из различных траекторий социально-экономического и научно-технического развития хозяйства страны, его региональных и межотраслевых комплексов, влияющих как на объем производства, так и на его транспортоемкость и факторы территориальной неравномерности. Обозначим такого рода условия:

F₁- условия, обеспечивающих максимальную транспортную потребность (спрос);

F_n - условия, обеспечивающие минимальную потребность;

F_j - промежуточные условия.

На фоне этих неопределенных условий возможны решения множества E, где:

E₁ - выбор производительности (или других, в т.ч. качественных

характеристик) из соображений максимальных объемов в течение длительного периода;

E_m - выбор характеристик системы в предположении минимальной потребности;

E_i - промежуточные решения.

Тогда результатом решения e_ij является оценка, соответствующая варианту E_i - и условиям F_j. Основной смысл оценки e_ij- выигрыш, т.е. чистый результат, понимаемый как полезность за вычетом возникающих в ходе решения i в ситуации j потерь.

Такое семейство решений представляется в виде матрицы решений (таблица 1).

Таблица 1- Матрица решений

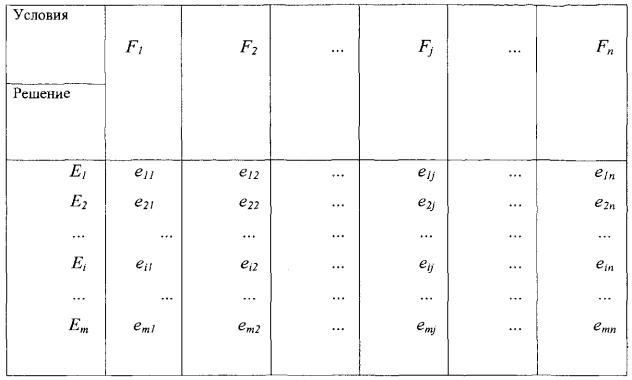
К такой структуре применимы, прежде всего, теоретико-игровые подходы на основе введения различных оценочных функций. Оценочная функция каждому варианту решения E_i приписывают некоторое значение e_i2, который характеризует решение E_i в целом, с учетом всех возможных в зависимости от F последствий.

Способ построения оценочной функции зависит от критерия выбора, который предполагается применить к этой функции. Например, можно оценочную функцию принять как аддитивную, относительно взвешенных наибольшего и наименьшего результатов:

(2)

где a и b весовые коэффициенты (уровни значимости). Тогда наилучший выбор представится в виде:

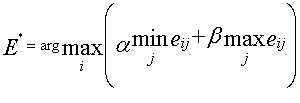(3)

Наиболее простыми оценочными функциями, представленными, в частности, в работе /2/ являются 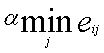и а также функция математического ожидания 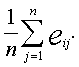Выбор варианта на их основе заключается в нахождении минимального или максимального значения такой оценочной функции. Это может быть выбор исходя из:

-нейтральной позиции:

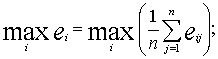
-пессимистической позиции:

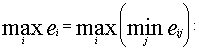
-осторожной позиции:

где - максимальный уровень возможных потерь.

Сила позиции в том, что для каждого иного внешнего состояния результат может быть равным этому, или лучшим;

-оптимистической позиции

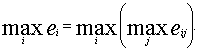
Основная формальная структура принятия решения /3/ предусматривает установление отношений частичного порядка. В графической интерпретации они представляются в виде прямоугольников в двумерном случае (два состояния внешней среды при множестве возможных решений) и в виде гиперконусов в n- мерном случае. При этом легко выделить конус предпочтения, где любое решение будет лучше, чем лежащие в вершине конуса, т.е. при любом стечении внешних обстоятельств исход таких решений будет более благоприятным. Противоположным относительно той же вершины будет антиконус. За пределами конуса предпочтения и антиконуса располагаются области неопределенности, где оценка решений возможна лишь на основе оценочной функции W на всем _n- мерном пространстве Rⁿ. Тогда каждому значению функции W соответствует некоторая гиперповерхность - поверхность уровня (в традиции микроэкономического анализа - поверхность безразличия).

Иллюстрация двумерного случая функции W(e_i1, e_i2) показана на рисунке 1.

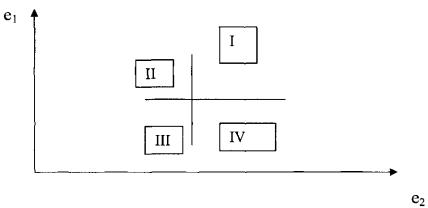
Рисунок 1 - Установление отношений частичного порядка для двумерного случая

На этом рисунке в поле оценок вариантов i в зависимости от внешней ситуации e_i, или e_i2 выделена произвольно точка, через которую проведены линии разбивающие все поле на конус предпочтения (I), антиконус (III) и области неопределенности (II и IV). Через эту произвольную точку проведены также три типа функции предпочтения, каждая из которых объединяет все варианты с одинаковым уровнем оценки W, справа и выше которой - более предпочтительные варианты, а слева и ниже - наоборот, менее предпочтительные.

Выводы

Этот базовый подход принят за основу и в предложенной постановке задачи организации региональной транспортной системы, где в качестве целевого функционала рассматривается функция благосостояния, максимизируемая на пространстве фазовых координат состояния транспортной системы при ресурсных ограничениях.

Литература

1. Абчук В.А., Бункин В.А. Интенсификация: принятие решений. - Лениздат, 1987

2. Вентцель Е.С. Введение в исследование операций. - М.: Советское радио, 1984.

3. Мушик Э., Мюллер П. Методы принятия технических решений. Пер. с нем. - М.: Мир, 1990. - 206 с.