УДК 621.314.572

      

    МОДЕЛИ ВИБРАЦИОННО-КОНТАКТНОГО КОНТРОЛЯ С ИСПОЛЬЗОВАНИЕМ ВИБРИРУЮЩИХ ПРЕОБРАЗОВАТЕЛЕЙ  

 

                                         Федотов А.И., Лисин С.К.

       СПб государственный политехнический университет, РОССИЯ

       СПб национальный минерально-сырьевой университет «Горный», РОССИЯ

 

                                                     Аннотация

          В статье рассматриваются модели вибрационно-контактного контроля физико-механических свойств технических объектов с помощью вибрирующих преобразователей. Исследованы математические модели, используемые для оценки и синтеза параметров нелинейных режимов (в том числе отклонений длин и перемещений) объектов технологического цикла. При этом оцениваемые параметры являются параметрами нелинейных численно решаемых систем уравнений, устанавливающих аналитическую связь между амплитудой, смещением центра колебаний и фазовым параметром измерительной вибрационной системы.

       Ключевые слова: модели контроля, нелинейные режимы, численные решения

 

          models vibratory contact control of properties of technical objects

                                

                                                   Fedotov A.I., Lisin S.K.

 

                                                           Abstract

 

         The article discusses models vibratory contact monitoring of physico-mechanical properties of technical objects using vibration transducers. A mathematical model used for the evaluation and synthesis of parameters of nonlinear modes (including deviations of lengths and displacements) of the objects of the technological cycle. Thus, the estimated parameters are parameters nonlinear numerically solve systems of equations that establish an analytical relationship between the amplitude, the offset of the center of oscillation and the phase parameter measuring the vibration system.

        Keywords: models control, nonlinear regimes, numerical solutions

 

         Развитие вибрационных, виброударных методов измерений и контроля свойств и параметров, в том числе контроля свойств объектов технологического цикла, связано с необходимостью построения теоретических моделей. Становятся актуальными задачи прогнозирования и анализа нелинейных динамических режимов, способствующих повышению точности и эффективности контроля требуемых параметров с помощью измерительных подвижных систем[1-2].

Рассмотрим математические модели колебаний подобных подвижных систем в режиме вибрационного контакта измерительного наконечника преобразователя с объектом контроля. При этом нелинейные численно решаемые математические модели будут реализованы как точными, так и приближенными методами. Функциональная схема одномерного вибрационно-контактного преобразователя содержит измерительный наконечник, соударяющегося с поверхностью контролируемого объекта. Одномерный преобразователь содержит мультивибратор и высокочувствительную генераторную систему. Подвижная сис­тема преобразователя имеет нелинейную динами­ческую характеристику, обусловленную существенным различием жест­кости упругого подвеса измерительного органа в зоне и вне зоны его контакта с поверхностью контролируемого изделия. Резонансный режим измерительного наконечника поддерживается мультивибратором измерительного преобразователя [3-5].

  Восстанавливающая характеристика  в интервалах упругой характеристики выражается двумя различными функциями и не является линейной функцией. Подобные функции, составленные из линеаризованных отрезков и остающиеся однозначными в отдельном закрытом интервале, получили название кусочно-линейных функций. При этом выражение  упругой характеристики в безразмерной форме для решений асимптотическим методом соответственно имеют вид:

                                

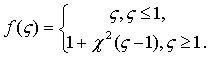
В соответствии с методом гармонического баланса соответствующее решение                         

 записывается в виде  . 

Здесь и - смещение центра и амплитуда колебаний,     . Уравнение , соответствующее координате системы  = 1 и фазовому параметру , имеет вид

                               .                                                         (1)

Система трансцендентных уравнений для определения искомых переменных ,  и методом гармонического баланса принимает вид:

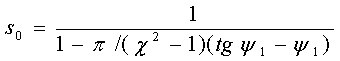                        ,                       (2)

 

                                                   (3)

 

                            .                                                 (4)      

Замкнутая нелинейная система (2), (3), (4) устанавливает аналитическую зависимость жесткости χ2 в виде функционала

 

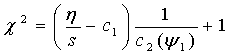                      .                                        (5)

Для применения метода измерения жесткости необходимо получить зависимость жесткости χ() с помощью решений системы (2), (3), (4), (5). Смещение центра колебаний  характеризует изменение амплитуды выходного сигнала преобразователя при изменении физико-механических свойств контролируемых объектов.

В общем виде областью определения функции точного решения  является интервал [, 1]. Здесь  – координата положения измерительного наконечника (), отсчитываемая от равновесного положения; Δ – зазор измерительной системы;  . Областью определения функций  и  является интервал [1, ].

Дифференциальное уравнение вынужденных колебаний на интервале  записывается в виде

                                   ,                                                             (6)

               где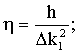            

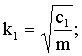
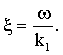
          Аналогично, используя принятые обозначения,  на интервале  имеем    

                            .                                                              (7)

Для определения точных периодических решений системы уравнений (6), (7) воспользуемся методом «припасовывания». Решения уравнений (6),(7) относительно , содержат произвольные постоянные интегрирования , , А3 , А4.

Следуя методу припасовывания, для уравнения (7) принимаем начальные условия:

                        ,                                                                  (8)

где – момент времени, соответствующий вхождению измерительного наконечника в контакт  с поверхностью объекта измерения. Конечные условия для уравнения (7):

                                                                                            (9)

где – момент выхода измерительного наконечника из фазы контакта.

Начальными условиями для уравнения (6), описывающего движение в фазе без контакта, будут условия (9). Следовательно, конечными условиями и одновременно условиями периодичности для уравнения (6) являются условия

                     , .                                                          (10)

 Неизвестными в периодических решениях являются постоянные интегрирования и параметры , , , . Максимальное отклонение измерительного наконечника от положения статического равновесия  вправо определяется из уравнения (7) и условий

                           ,   ,  .                                                        (11)

Максимальное отклонение измерительного наконечника от положения статического равновесия влево определяется из уравнения (6)     и условий

                           ,  , .                                                         (12)

        Рассматриваемые соотношения обеспечивают возможность определить амплитудно-частотные характеристики системы в режиме вибрационного контакта измерительного наконечника. Рассматриваемая  расчетная модель строится с учетом упругих свойств измеряемого объекта . Режиму вынужденных колебаний на фазовой плоскости соответствует замкнутая фазовая траектория, время пробега изображающей точки которой совпадает с периодом возмущающей силы.

       На рис. 1 представлен фазовый портрет установившихся режимов вибрационно-контактного преобразователя.

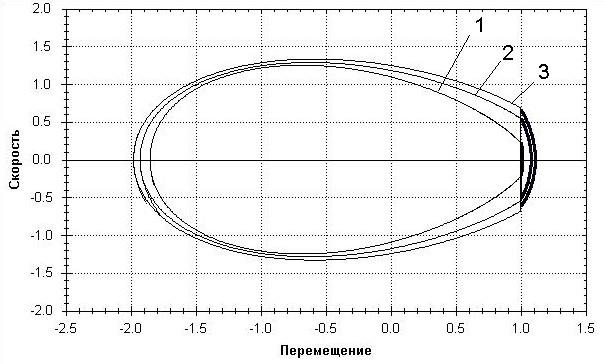
                                     Рис. 1. Фазовая диаграмма установившихся режимов

 

           В табл. 1приведены значения параметров вибрационно-контактных режимов одномерного измерительного преобразователя. Расчетная модель воспроизводит аналитическую связь параметра упругих свойств измеряемого объекта  с параметром s0 непосредственно измеряемым выходной ЭДС преобразователя..                                                                

                                                                                                                        

                                                                                                                                  Таблица 1

Режимы

η

ξ

α 2

α 1

s0

1

1.49

0.7

1.03

-1.854

1.013

0,41

2

1.5

0.7

1.04

-1.932

1.077

0,427

3

1.5

0.7

1.1

-1.96

1.108

0,426

 

Жесткость χ рассматриваемой системы является функцией параметров η, ξ, 1, s0. Среди них параметр s0 непосредственно измеряется. Неопределенность этого параметра носит характер статистической погрешности  и определяется через среднее квадратичное отклонение. Параметры η, ξ устанавливаются при тарировании измерительного вибрационно-контактного преобразователя и их неопределенности имеют характер систематической погрешности. Неопределенность параметра 1 контролируется специальными средствами [4]. Поэтому стандартная неопределенность типа В вычисляется как для случая однократного измерения по градуированной шкале с учетом погрешности, определяемой классом точности данного средства измерений.

Неопределенность жесткости χ получается по правилу получения неопределенности косвенных измерений, то есть путем переноса неопределенностей в значениях параметров на  неопределенность искомого параметра.

 

Литература:

1. Вибрации в технике. Защита от вибраций и ударов; Т.6: Справочник / Под ред. К.В. Фролова/. М.: Машиностроение, 1981. - 456 с.

2. Закржевский М.В. Колебания существенно-нелинейных систем.- Рига: Зинатне, 1980. - 190 с.

3. Лисин, С.К. Использование теории переноса ошибок при оценке параметров нелинейных систем/ С.К. Лисин, А.И. Федотов// Научно – технические ведомости.  – 2009. - № 3. - С. 181-184.

 4. Федотов, А.И. Теория измерений /А.И. Федотов, С.К. Лисин, Г.С. Морокина. – СПб.: Изд-во Политех. ун-та, 2013. – 325 с.          

5. Патент РФ Ru– 2016374. Виброконтактный преобразователь для линейных измерений/ Б.А. Глаговский [и др.]. – Опубл. 15.07.94, Бюлл. № 13.