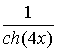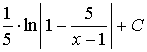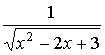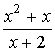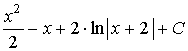Педагогические науки / Современные методы преподавания

к.т.н. Нікулін О.В., к.ф.-м.н. Наконечна Т.В.

Дніпродзержинський державний технічний університет, Україна

Дніпропетровський національний університет ім. О. Гончара, Україна

Тестування при навчанні математики в університеті

Вступ. В Україні продовжуються роботи з модернізації вищої освіти та інтеграції до європейського освітнього простору. Зміни в освіті вимагають удосконалення математичної та взагалі фундаментальної підготовки. Зокрема математика та інформаційні технології є засобами, сприяючими вивченню студентами фундаментальних наук та спеціальних дисциплін. Тому якісна університетська освіта вимагає якісного навчання математики.

В процесі навчання важливим є модульний та підсумковий контроль успішності, який потрібно проводити ефективно [1]. В основі розв’язання проблеми може бути декомпозиція дій з використанням тестування та інформаційно-комунікаційних технологій (ІКТ). У пропонованої роботі увага приділяється в основному до першої складової.

Важливі етапи математичної підготовки у вищих навчальних закладах пов’язані з такими розділами математики, як лінійна алгебра, математичний аналіз, теорія звичайних диференціальних рівнянь тощо, які потім широко використовуються при математичному моделюванні. Як правило, при модульної організації процесу навчання з математики цим розділам відводяться окремі змістовні модулі. У рамках кожного з них проводяться модульні контрольні, отже, питання методичного забезпечення і використання тестів є актуальними.

Постановка задачі. До методичного забезпечення з математики висувається низка вимог. «Загальне розуміння проблеми покращення підготовки майбутнього фахівця у вищому навчальному закладі потребує аналізу сутності його професійної компетентності з точки зору ефективності професійної діяльності. Запровадження компетентісного підходу до модернізації змісту вищої освіти потребує відбору змісту дисциплін, який може забезпечити формування компетентностей; розробки системи контролю за їх формуванням»[2]. Але в сучасних умовах викладачі здійснюють навчання, коли, по-перше, постійно зростає обсяг інформації, який повинні засвоїти студенти, по-друге, фактично має місце скорочення часу аудиторних занять та зростає обсяг самостійної роботи. Вказану суперечність можна усунути за рахунок використання інтенсивних технологій навчання, таких як тестування та ІКТ, підручників і посібників, що відповідають викликам часу.

До теперішнього часу в Україні був розроблений і апробований ряд підручників і навчальних посібників з вищої математики та її застосувань при підготовці бакалаврів [3-5]. За результатами огляду відомих варіантів тестів можна зробити висновок, що у більшості спостерігається їх тісний зв'язок з розрахунковими завданнями. Для оцінки успішності розв'язання потрібна трудомістка перевірка їх викладачами, причому сам процес вирішення студентами - трудомісткий. В результаті кількість задач у завданні досить мала і виникають сумніви в повноті перевіреного засвоєння розділу курсу.

Метою роботи вибрано вдосконалення структури та змісту тестів з різних розділів математики, щоб забезпечити їх репрезентативність, зниження трудомісткості розв'язання і можливість автоматизації перевірки.

Результати роботи. З урахуванням педагогічних і психологічних аспектів тестування студентів використовуються напрацювання незалежного зовнішнього оцінювання з математики, представляється доцільним врахувати досвід і результати розробки структури тестів та організації оцінювання. Відповідний матеріал по формі, змісту і структурі був представлений в збірнику тестових завдань [6] та посібнику [7] з грифом МОН України. Студенти виконують письмові або електронні контрольні роботи протягом 90 хвилин аудиторних занять.

До модульної контрольної роботи включаються закриті тести, тести відповідності та тести з короткою числовою відповіддю. У порівнянні з варіантами контрольних з [6, 7] в кожен з них додаються тести відповідності. В кожної контрольної роботі студентові пропонується варіант завдання з декількох десятків структурних одиниць, з них на тести відповідності відводиться вісім одиниць, тобто два завдання. В тестах відповідності заповнюються відповідні таблиці. Далі розташовані тести з короткими числовими відповідями. Можлива автоматизація процесу тестування як на етапі виконання завдань (робота в комп'ютерному класі), так і при їх перевірці та з урахуванням наданих ресурсів (комп'ютерне забезпечення та час роботи). У підсумку студентом заповнюється бланк (електронний або паперовий).

В кожному з варіантів передбачається до десяти завдань-тестів закритого типу, наприклад,

Яка з наведених прямих проходить через початок координат?

а	б	в	г

Відповідь: б: , дійсно .

Приклад тесту відповідності. Установіть відповідність між функціями (1– 4) та невизначеними інтегралами від цих функцій (А–Д).

Відповідь:

Функція	Інтеграл		А	Б	В	Г	Д
1.	А	1
		2
2.	Б	3
		4
3.	В
4.	Г
	Д

Приклад відкритого тесту. При якому значенні параметра пряма поділяє площу фігури, обмеженої лініями 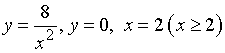у відношенні 2:1?

Розв’язання. Спочатку побудуємо вказану область. Позначимо через площу фігури, яка обмежена кривою , віссю абсцис та прямою . Обчислення цієї площі приводить до невласного інтеграла

.

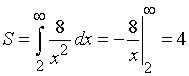За умовами задачі нам необхідно (рис.1) підібрати таке значення параметра , для якого

.

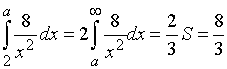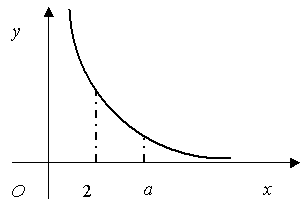
Рисунок 1. Визначення параметру

Тоді

.

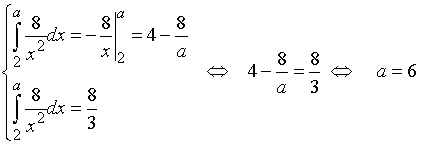Відповідь: .

Тести подібної структури, запропоновані для проведення модульних контрольних робіт, представлені в посібнику з вищої математики [8]. При апробації по них виконувалося тестування результатів навчання вищої математики в Дніпродзержинському державному технічному університеті та в інституті підприємництва «Стратегія» (м. Жовті Води), Дніпропетровському національному університеті ім. О.Гончара в 2008 - 2015 навчальних роках. При перевірці бланків відповідей (рис.2) підтверджені очікувані позитивні результати інновації за рахунок скорочення трудомісткості оцінювання та підвищення об'єктивності отриманих результатів.

БЛАНК ВІДПОВІДЕЙ

Тести закритого типу

1) 2) 3) 4)

5) 6) 7)

Рисунок 2. Фрагмент бланка відповідей

У порівнянні з [6] варіанти тестів були доопрацьовані. Додані один-три тести відповідності із заповненням для кожного таблиці розміром 4х5. Контрольна робота завершується кількома (до трьох) завданнями з короткими відповідями (рис. 3).

Тести закритого типу

Задача 1

Задача 2

……………………………………………………………….

Задача 7

Тести відповідності

Задача 8

	А	Б	В	Г	Д
1
2
3
4

Задача 9

	А	Б	В	Г	Д
1
2
3
4

Тести відкритого типу

Задача 10

,

Задача 11

,

Задача 12

,

Рисунок 3. Типова структура тестового варіанта

Висновки. Вирішення проблем модернізації освіти в Україні включає вдосконалення фундаментального навчання, зокрема, з математики. Зміни в системі вищої освіти та ії математичної складової вимагають модернізації або розробки нових посібників. Використання підручників і посібників нового покоління приводять до зміни технології навчання. Реалізація відповідних програм вимагає застосування нових або видозмінених методик, наприклад, при контролі навчання. Активізація математичної підготовки майбутніх фахівців в сучасних умовах ґрунтується у тому числі на тестуванні та використанні освітніх інформаційно-комунікаційних технологій. Вони дають змогу індивідуалізації навчання як за обсягом, так й за темпом, мобільного контролю засвоєння знань та набуття відповідних компетенцій.

Розроблені та підготовлені для подальшого використання тести для змістовних модулів [6]. Книга [8] вміщує не тільки основні факти і формули з математики, а також тестові задачі трьох основних видів, готується до публікації перевидання навчального посібника з доопрацьованими тестами.

Література

1.Алексеев А.Н. Дистанционное обучение инженерным специальностям: Монография / А.Н. Алексеев. – Сумы: ИТД «Университетская книга», 2005. – 333 с.

2.Драч І.І. Компетентісний підхід як засіб модернізації змісту вищої освіти // Проблеми освіти: Наук. зб. – К. , 2008. –  Вип. 57. – С. 44 – 48.

3.Антоненко В.Ф. Вища математика. Модуль 1. Лінійна алгебра: Навч. посібник / В.Ф. Антоненко, Т.І. Олешко, Ю.А. Паламарчук. За заг. ред. проф. Т.І. Олешко. – К.: Книжкове вид-во НАУ, 2005. – 140 с.

4.Кравченко В. В. Вища математика. Модуль 2. Векторна алгебра та аналітична геометрія: Навч. посібник / В.В. Кравченко, Т.В. Лубенська, Т.І. Олешко. За заг. ред. проф. Т.І. Олешко. – К.: Книжкове вид-во НАУ, 2005. – 144 с.

5.Вища математика: Підручник: У 2 кн. – 2-ге вид., перероб. і доп. – К.: Либідь, 2003. – Кн. 1. Основні розділи / Г. Й. Призва, В. В. Плахотник, Л.Д. Гординський та ін.; За ред. Г. Л. Кулініча . – 400 с.

6.Шумейко О. О. Модульне і підсумкове оцінювання: тести з вищої математики/ О.О. Шумейко, Т.В. Наконечна, О.В. Нікулін. ‒ Дніпропетровськ:  «Наука і освіта», 2009. – 172 с.

7.Огурцов А.П. Вища математика для підготовки бакалаврів з інженерії: навч. посіб.: у 3 ч. Ч.3: Ряди. Елементи теорії ймовірностей та математичної статистики. Комплексний аналіз. Операційне числення / А.П. Огурцов, Т.В. Наконечна, О.В. Нікулін; за заг. Ред.. А.П. Огурцова. – 2-ге вид., виправл. та доповн. – Д.: Біла К.О., 2010. – 434 с.

8.Нікулін О.В. Вища математика: факти і формули, задачі і тести: Навч. посіб. / О.В. Нікулін, Т.В. Наконечна. – Дніпропетровськ: Біла К.О. – 2015. – 188 с.