Физика /1.Теоретическая физика
К.п.н. Мищик С.А.
Государственный морской университет имени
адмирала Ф.Ф.Ушакова ,
Россия
Системные колебательные задачи
прикладной физики морского флота
Системные колебательные задачи
прикладной физики морского флота отражают целостно-системное моделирование
основных элементов транспортных объектов. При этом возникает ориентация на
единство базисных характеристик предметных и исполнительных условий
относительно предмета содержания и способа его реализации. Рассматриваются: свободные, вынужденные и затухающие колебания
элементов морских систем в различных внешних средах с расчётами амплитудных,
временных, динамических и кинематических параметров под действием сил
сопротивлений, имеющих функциональную
пространственно-временную зависимость на морском флоте.
В процессе решения системных колебательных
задач прикладной физики морского флота необходимо применять основные положения
теории деятельности, системного анализа и теории формирования интеллекта.
Системный анализ предполагает
выполнение последовательности системных аналитических действий: выделить объект
анализа – колебательную задачу прикладной физики морского флота (КБЗПФМФ) как
систему; установить порождающую среду КБЗПФМФ; определить уровни анализа КБЗПФМФ;
представить целостные свойства КБЗПФМФ относительно пространственных, и временных
характеристик и их комбинаций; выделить структуру уровня анализа КБЗПФМФ;
установить структурные элементы уровня анализа КБЗПФМФ; определить
системообразующие связи данного уровня анализа КБЗПФМФ; представить
межуровневые связи анализа КБЗПФМФ; выделить форму организации КБЗПФМФ;
установить системные свойства и поведение КБЗПФМФ.
Задача 1
|
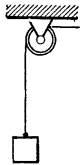
При разгрузке судна груз массой m=2 тонны равномерно опускается со скоростью V=5
м/с. Определить наибольшее натяжение троса при резкой остановке спуска, если
коэффициент жесткости троса k
= 40 кН/см. Массу троса не
учитывать. Ответ: 471 кН. |
|
Задача 2
|
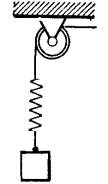
При разгрузке судна груз массой m=2 тонны равномерно опускается со скоростью V=5
м/с. Для уменьшения нагрузки на трос введена демпфирующая пружина с
жёсткостью k1 = 4
кН/см. Определить наибольшее
натяжение троса при резкой остановке спуска, если коэффициент жесткости троса
k = 40 кН/см. Массу троса не учитывать. Ответ: 156 кН. |
|
Задача 3
Определить период свободных колебаний фундамента судового
двигателя, поставленного на упругое основание судовой переборки, если масса
фундамента с двигателем m = 90 тонн,
площадь подошвы фундамента S = 15 м2, коэффициент
жесткости судовой переборки c = λ·S, где грунта λ
= 30Н/см3—удельная жесткость основания судовой переборки.
Ответ: Т = 0,09 с.
Задача 4
Найти период свободных вертикальных колебаний судна на
тихой воде, если водоизмещение судна m = 50000 тонн, площадь горизонтального сечения в
плоскости ватерлинии S = 3500 м2 и не
зависит от высоты сечения. Плотность морской воды 1030 кг/м3.
Силами, обусловленными вязкостью воды, пренебречь.
Ответ: Т = 7,47 с.
Задача 5
Для определения сопротивления воды движению модели
судна при очень малых скоростях модель М пустили плавать в сосуде, привязав нос
и корму посредством двух одинаковых пружин А и В, силы натяжения которых
пропор- циональны удлинениям. Результаты наблюдений показали, что отклонения
модели от положения равновесия после каждого размаха уменьшаются, составляя
геометрическую прогрессию, знаменатель которой равен 0,9, а продолжительность
каждого размаха Т = 0,5 сек. Определить силу R сопротивления воды, приходящуюся
на каждый Ньютон веса модели при скорости V=1 см/с, предполагая, что
сопротивление воды пропорционально первой степени скорости.

Ответ: R = 4,3 мН.
Задача 6
Найти уравнение движения модели судна при очень малых
скоростях, если модель судна М пустили плавать в сосуде, привязав нос и корму
посредством двух одинаковых пружин А и В, силы натяжения которых
пропорциональны удлинениям. Результаты наблюдений показали, что отклонения
модели от положения равновесия после каждого размаха уменьшаются, составляя
геометрическую прогрессию, знаменатель которой равен 0,9, а продолжительность
каждого размаха Т = 0,5 с. В начальный момент пружина А была растянута, а пру- жина
В сжата на величину Δℓ = 4см и модель была отпущена без начальной
скорости.

Ответ: ![]() .
.
Задача 7
|
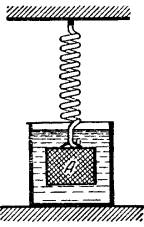
Для определения вязкости судового моторного
масла применяют метод Кулона: тонкая
пластинка А на пружине сначала колеблется в воздухе, а затем в судовом
моторном масле, вязкость которого необходимо определить. Рассчитываются
периоды колебаний: T1 — в первом случае и T2
— во втором. Сила трения между пластинкой и жидкостью задаётся
формулой F тр = 2SkV, где 2S — общая площадь поверхности
пластинки, V — ее скорость, k — коэффициент вязкости.
Пренебрегая трением между пластинкой и воздухом, определить коэффициент k
по найденным из опыта величинам T1 и T2
если вес пластинки в воздухе равен Р. Ответ:
|
|
Задача 8
Спасательный
круг массой 5 кг подвешен на тросе, коэффициент жесткости которого равен
20 Н/см. Сопротивление морской воды пропорционально скорости. Амплитуда движения
спасательного круга после четырех
колебаний уменьшилась в 12 раз. Определить период колебаний спасательного круга и логарифмический декремент затухания.
Ответ: Т = 0,319 с; D = 0,311.
Задача 9
При гравитационной обсервации подводных объектов для
определения ускорения силы тяжести в данном месте земного шара производят два
измерения. К концу пружины подвешивают груз P1 и измеряют статическое удлинение пружины ℓ1. Затем к концу этой же пружины подвешивают другой
груз P2 и опять измеряют статическое удлинение ℓ2. После этого повторяют оба измерения, заставляя оба
груза по очереди совершать свободные колебания, и измеряют при этом периоды
колебаний T1 и T2. Второе измерение делают для того, чтобы учесть
влияние массы самой пружины, считая, что при движении груза это влияние
эквивалентно прибавлению к колеблющейся массе некоторой добавочной массы. Найти
формулу для определения ускорения силы тяжести по этим результатам измерений.
Ответ: 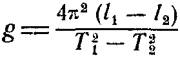 .
.
Задача 10
Причальная бочка массой 4 тонны находится на
поверхности моря, уровень которой в месте нахождения бочки изменяется
вследствие волнения по закону
![]() (t — в секундах; s — в метрах).
(t — в секундах; s — в метрах).
Считая горизонтальное сечение причальной бочки
постоянным по высоте и равным 5 м2, определить ее вертикальные колебания относительно
уровня спокойной воды, если плотность морской воды равна 1030 кг/м3. В начальный момент причальная бочка находилась на уровне
спокойной воды, и ее абсо-лютная скорость была равна нулю. Сопротивлением воды
пренебречь.
Ответ: Х=![]() м.
м.
Задача 11
Определить установившиеся колебания причальной бочки
относительно колеблющегося уровня воды, если сила сопротивления воды
пропорциональна первой степени скорости причальной бочки, причем коэффициент
пропорциональности равен 16 кН·с/м. Причальная бочка массой 4 тонны
находится на поверхности моря, уровень которой в месте нахождения бочки
изменяется вследствие волнения по закону
![]() (t — в секундах; s — в метрах).
(t — в секундах; s — в метрах).
Горизонтальное сечение причальной бочки постоянно по
высоте и равно 5 м2, плотность морской воды равна 1030 кг/м3. В начальный момент причальная бочка находилась на уровне
спокойной воды, и ее абсолютная скорость была равна нулю.
Ответ:
Х=![]() м .
м .
Задача 12
При расчете бортовой качки судна для учета инерционных
сил морской воды момент инерции судна принимают равным J + μ, где J
— собственный момент инерции судна, a μ — присоединенный момент
инерции. Для определения μ динамически подобную модель
судна подвергают воздействию внешнего гармонического момента Mo sin pt (Мо — постоянная). Изменяя
частоту р, добиваются появления максимальных амплитуд (при p = p1
максимальная амплитуда равна а). Принимая, что восстанавливающий
момент равен mghφ (m — водоизмещение масса судна, h
—метацентрическая высота) и что момент сопротивления пропорционален угловой
скорости судна при качке, определить присоединенный момент инерции μ
.
Ответ: 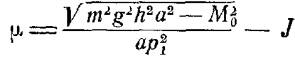
Задача 13
|
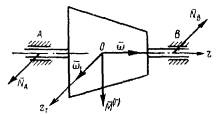
Ротор судовой турбины, ось которого расположена в
диаметральной плоскости судна и параллельна продольной его оси, вращается со
скоростью n = 3000 об/мин. Масса ротора m = 4000 кг, его радиус инерции относительно оси
вращения ρ = 0,6 м, расстояние ℓ между
подшипниками А и В равно 2 м. Судно имеет килевую качку с амплитудой φо =
π/30 и периодом T = 8
сек. Определить величины максимальных гироскопических давлений на подшипники.
Ответ: 18,61 кН . |
|
Задача 14
Ареометр массой m=0,2 кг плавает в судовом моторном масле. Если его
немного погрузить в судовое моторное масло и отпустить, то он начнет совершать
колебания с периодом T=3,4 с. Считая колебания незатухающими,
найти плотность судового моторного масла ρ, в котором плавает ареометр. Диаметр
вертикальной цилиндрической трубки ареометра d=l см.
Ответ: ρ = 890 кг/м3.
Задача 15
Как изменится период вертикальных колебаний груза,
висящего на двух одинаковых грузовых морских тросах, если от последовательного
соединения грузовых морских тросов перейти к параллельному их соединению?
Ответ: уменьшится в 2 раза.
Задача 16
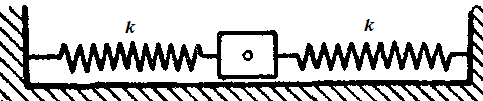
Груз массой m=5 тонн,
лежащий на горизонтальной палубе судна, укреплён двумя горизонтальными
найтовами одинаковой жесткости k = 2
кH/см. В результате бортовой качки груз был сдвинут на 4 см от положения
равновесия вправо и начал движение по палубе без начальной скорости. Найти
уравнение движения, период колебаний, а также максимальную скорость груза. Силу
трения не учитывать.
Ответ: 1) х = 0,04 cos 28,3t (м); 2) Т =
0,22 с; 3) V max = 1,1 м/с .
Задача 17
Рассчитать силы, действующие во время бортовой качки
на тяжеловес массой m=30
тонн, установленный в носовой части верхней палубы между грузовым люком и
фальшбортом, если период бортовой качки Тθ = 18 с, высота
волны hВ = 2r0
= 6 м, координаты центра тяжести груза относительно центра масс судна: x = 0,6 м, y = 7 м,
z = 12 м. Размер груза прямоугольной формы вдоль судна ℓ
= 5 м, поперёк судна b = 3 м,
высота груза прямоугольной формы h1
= 3 м. Высота фальшборта 1,6 м.
Ответ: суммарная сила, действующая на тяжеловес в поперечном
направлении FY = 207 кН; максимальная суммарная составляющая сил
инерции и силы тяжести, действующая по оси OZ, PZ = 232 кН.
Задача 18
Рассчитать силы, действующие во время килевой качки на
тяжеловес массой m=30
тонн, установленный в носовой части верхней палубы между грузовым люком и
фальшбортом, если период килевой качки Тψ = 8 с, высота
волны hВ = 2r0
= 6 м, координаты центра тяжести груза относительно центра масс судна: x = 0,6 м, y = 15 м,
z = 12 м. Размер груза прямоугольной формы вдоль судна ℓ
= 5 м, поперёк судна b = 3 м,
высота груза прямоугольной формы h1
= 3 м.
Ответ: суммарная сила, действующая на тяжеловес в продольном
направлении Fx = 81 кН; суммарная сила, действующая на тяжеловес в
поперечном направлении FY = 232 кН; максимальная суммарная составляющая сил инерции и силы
тяжести, действующая по оси OZ, PZ = 214 кН.
Задача 19
Рассчитать максимальную и минимальную силы,
действующие во время вертикальной качки на горизонтальную палубу судна, на
которой находится тяжеловес массой m=20
тонн, если период вертикальной качки cудна равен
Т=16
секунд и амплитудой волны hВ = 4 м.
Ответ: Fmax =
208,6 кН ; Fmin =
183,8 кН .
Задача 20
Морское судна имеет ширину В=16 м и за t=80 секунд совершает n=5 полных бортовых колебаний. Аппликата метацентра
судна Zm=8,3 м. Коэффициент класса морского судна равен С=0,8.
Определить аппликату центра тяжести судна ZG .
Ответ: ZG =7,66 м .
Задача 21
Морское судно имеет длину L=140 м, ширину В=20 м, осадку Т=8,5 м, коэффициент полноты
водоизмещения δ = 0,8; коэффициент полноты ватерлинии α=0,85;
аппликату центра тяжести судна ZG=8,4 м; поперечную метацентрическую высоту h=1,5 м; продольную метацентрическую высоту H=150 м; если коэффициент, учитывающий присоединённые
массы воды при бортовой качке, равен k1=0,3;
а коэффициент, учитывающий присоединённые массы воды при килевой качке, равен k2=1,01.
Плотность морской воды в точке измерения равна ρ=1010 кг/м3.
Ответ:
Т1=14,1
с; Т2=7,9 с.
Задача 22
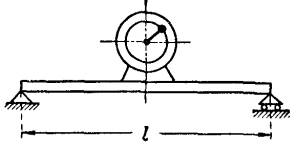
Определить вынужденные колебания cудового двигателя массой m=1,5 тонны, укреплённого посередине двух положенных
рядом двутавровых балок № 30 с моментами инерции поперечного сечения J=8881 см4 и пролетом ℓ=10 м, пренебрегая весом балок
и считая их свободно лежащими, если эти колебания вызываются равномерным
вращением вала двигателя, на котором укреплен противовес массой m1 = 0,4 кг на расстоянии r=5 см
от оси вращения, если угловая скорость вала ω = 25 с -1 .
Ответ: у** = 0,0017 sin 25t (см).
Задача 23
Найти угловую скорость вала судового двигателя, при
которой возникает резонанс, если его масса m=1,5 тонны и он укреплён посередине двух положенных
рядом двутавровых балок № 30 с моментами инерции поперечного сечения J=8881 см4 и пролетом ℓ=10 м. Весом балок пренебречь
и считать их свободно лежащими. Колебания вызываются равномерным вращением вала
двигателя, на котором укреплен противовес массой m1 = 0,4 кг на расстоянии r=5 см
от оси вращения.
Ответ:
ωкр
= 33,4 с -1 .
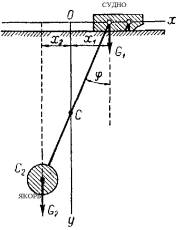
Задача 24
Морское судно водоизмещением m1 имеет
горизонтальную качку на тихой воде. Адмиралтейский якорь массой m2 подвешен
на якорной цепи длиной ℓ. Найти уравнение движения морского
судна и период качаний адмиралтейского якоря при условии, что в начальный
момент якорь отклонен на угол φ0
от вертикали и система «судно-якорь» находится в состоянии покоя. Вертикальную
ось провести через начальное положение центра тяжести системы «судно-якорь». Массой якорной цепи и силой сопротивления
среды пренебречь.
 Ответ:
Ответ: ![]() ;
; ![]() .
.