Экономика/Математические методы в экономике

Садыков В.М., Нехорошева В.А.

Автомобильно-дорожный институт ГВУЗ «ДонНТУ»

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ

Математическое моделирование играет огромную роль в задачах экономического планирования и прогнозирования. Это обуславливается, в первую очередь, принципиальной невозможностью экспериментов в экономике и важностью соответствующих задач.

В данной работе рассматриваются задачи, в которых управление понимается в классическом смысле, а именно: имеется объект управления- рассматриваемая динамическая система, и управляющая система – подсистема изучаемой системы, использующая информацию о состоянии внешней среды и информацию о состоянии объекта управления для выработки управляющего воздействия. Выработанное тем или иным образом управляющее воздействие изменяет параметры системы таким образом, чтобы можно было достичь заранее поставленной цели.

Исследованиями в этой сфере занимаются О.А. Дмитриева,

А.В. Смирнов и В.М. Глушкова и т.д.

Многие предприятия по-прежнему испытывают трудности, связанные с падением объемов производства и рентабельности продаж, потерей традиционных рынков сбыта продукции и затруднениями в поиске новых, слабой согласованностью в действиях высшего звена управления, отсутствием четко выраженных направлений развития, недостаточностью освоения новых видов продукции и новых технологий управления. Преодоление этих трудностей осуществляется в основном интуитивно, без опоры на научно обоснованные системы поддержки принятия решений, и носит формально-констатирующий, а не утверждающий характер.

     При таком подходе сложно не только объективно оценивать состояние управленческого процесса, но и определять тенденции его развития и вносить в него необходимые коррективы. Возникает противоречие между меняющимся содержанием хозяйственной деятельности и отстающим по темпам совершенствования управлением на предприятиях [1].

Цель – разработать динамическую модель экономической системы, адекватно реагирующую на изменяющиеся условия в стране.

Задачи:

· выявить факторы, влияющие на экономическое состояние страны;

· изучить текущее состояние экономики;

· рассмотреть методы, применяемые к данной системе и выявить наиболее практически ценные;

· разработать динамическую систему, максимально отвечающую текущему состоянию экономики.

Пусть эволюция во времени дискретной динамической системы (ДС) и ее канала измерения описывается уравнениями

x_k+1 = A_kx_k + f_k(u_k),      (1)

y_k = h_k^Tx_k + ξ_k.               (2)

Здесь k = 0, 1, …— дискретное время; x_k — недоступный непосредственному изменению n-мерный вектор состояния, x_k Î Rⁿ; Rⁿ — n-мерное вещественное еквилидово пространство; u_k — известный вектор управления, u_kÎ R^m, m ≤ n; y_k — вектор наблюдаемых сигналов, представляющих собой результаты измерения выхода объекта h_k^Tx_k, зашумленного действием аддитивной помехи ξ_k, y_k^T = (y_1k,…,y_mk), ξ_k^T =(ξ_1k,…, ξ_mk); T — символ операции транспонирования;

A_k и h_k^T= — известные матрицы размерностей n´ n и m´ n соответственно, det A_k ¹ 0 "k = 0, 1,…, h_ik Î Rⁿ; f_k( u_k ) — заданная n-мерная функция.

Предполагается, что помеха ξ_k удовлетворяет ограничениям по компонентам или по норме

ξ_ik² ≤ c_ip², i = 1,…, m, k = 0, 1, …, (3)

(ξ_ik – ξ_i,k-1)² ≤ c_ir², i = 1,…, m, k = 1, 2, …, (4)

ξ_k^Tξ_k ≤ c_p², k = 0, 1, …, (5)

(ξ_k – ξ_k-1)^T(ξ_k – ξ_k-1) ≤ c_r², k = 1, 2, …, (6)

где c_ip ,c_i, c_ir, c_r — заданные константы.

В предположении, что результаты текущих измерений y_k, k =0,1,. , известны, ставится задача эллипсоидального оценивания неизвестного вектора состояния x_k в виде

x_k Î E[ , H_k] = E_k ,

где E[ , H_k] ={x: σ(x, , H_k) ≤ 1}, σ(x, , H_k) = (x - )^TH_k^-1(x - ), — центр эллипсоида, H_k = H_k^T > 0. Параметры априорного эллипсоида ,

H_k при k = 0 полагаются заданными.

На ряду с дискретной ДС (1), (2) рассматривается задача эллипсоидального оценивания вектора состояния x_k непрерывной ДС

,              (8)

y_k = h_k^Tx_k + ξ_k                       (9)

по дискретным измерениям ее выхода y_k = y(t_k) в моменты времени t = t_k, t_k+1=t_k+T, T — интервал дискретности измерения и изменения управления.

Здесь t — непрерывное время, t Î [0, ∞); x_k = x(t_k) и ξ_k = ξ (t_k) — недоступный непосредственному измерению неизвестный вектор состояния и помеха измерения; h_k^T =h^T(t_k); C(t), D(t) — заданные для всех t ≥ 0 матрицы соответствующих размерностей с ограниченными непрерывными элементами. Остальные предположения соответствуют свойствам дискретной системы (1), (2).

Оценивание состояния дискретных ДС. Из уравнений (1), (2) непосредственно получаем

ξ_k = y_k - h_k^Tx_k ,                (10)

ξ_k-1 = y_k-1 - h_k-1^Tx_k-1 .         (11)

Воспользовавшись уравнением (1), из (10) и (11) находим

ξ_k - ξ_k-1 = z_k- r_k^Tx_k,           (12)

где z_k=(z_1k,…,z_mk)^T= y_k - y_k-1 – h_k-1^TA_k-1^-1f_k-1(u_k-1), r_k^T= =h_k^T-h_k-1^TA_k-1^-1.

Введя обозначение ζ_k = ξ_k - ξ_k-1, соотношение (12) формально можно представить как дополнительный канал измерения системы (1)

z_k=r_k^Tx_k+ ζ_k,             (13)

где помеха ζ_k = (ζ_1k, …, ζ_mk)^T удовлетворяет ограничениям по компонентам или по норме

ζ_ik² ≤ c_ir², i = 1,…, m, k = 1, 2, …, (14)

ζ_k^Tζ_k ≤ c_r², k = 0, 1, …, (15)

Исследуем случай покомпонентного ограничения помех. Рассмотрим множества

S_ip(x_k) = {x_k: (y_ik – h_ip^Tx_k)²≤c_ip², k = 0, 1,…, i =1, …m},     (16)

S_ir(x_k) = {x_k: (z_ik – r_ik^Tx_k)²≤c_ir², k = 1, 2,…, i =1, …m},     (17)

Соотношения (16), (17) определяют в фазовом пространстве системы (1), (2) множества S_ip(x_k) и S_ir(x_k) ее состояний, совместимые с результатами измерений. Эти множества представляют собой 2m гиперполос, каждая из которых ограничена двумя попарно параллельными гиперплоскостями

y_ik-h_ik^Tx_k=±c_ir, i =1, …m.

Очевидно, что для неизвестного вектора состояния системы (1), (2) x_k выполняется включение x_k Î D(x_k), где D(x_k)– пересечение всех 2m гиперполос множеств (16), (17). При этом, согласно предположению, выполняется также включение (7). Поэтому выполняется и включение x_k Î E[ ],

где E[ ] – эллипсоид вида (7) такой, что D(x_k)∩E[ ]Ì E[ ]. Для построения эллипсоида E[ ] целесообразно воспользоваться робастным алгоритмом последовательного построения 2m эллипсоидов, содержащих пересечения эллипсоидов с гиперполосами S_ip(x_k), i = 1, …m и S_ir(x_k), i = m+1, …, 2m.

Для случая (4) помеха ξ_k и скорость ее изменения по норме множества состояний системы (1), (2), совместимые с результатами измерений, ограничиваются соотношениями

S_p(x_k)={x_k:(y_k – h_k^Tx_k)^T(y_k – h_k^Tx_k)≤c_p²,   (18)

S_r(x_k)={x_k:(z_k – r_k^Tx_k)^T(z_k – r_k^Tx_k)≤c_r²,   (19)

Эти множества представляют собой цилиндры в фазовом пространстве Rⁿ системы (1), (2). Для ее неизвестного вектора состояния выполняется включение x_kÎD(x_k), гдеD(x_k)=S_p(x_k)∩S_r(x_k). Из предположения о выполнении условия (7) непосредственно следует включение x_kÎD(x_k)∩E[ ].

Поэтому оценивающий эллипсоид, гарантированно содержащий неизвестный вектор x_k, может быть построен с помощью эллипсоидальной аппроксимации пересечения E[ ] с множеством S_p(x_k) и затем аппроксимации пересечения полученного эллипсоида с множеством S_r(x_k). При этом оценивание вектора состояния системы (1), (2) сводится к построению параметрических семейств эллипсоидов  и  вида (7), содержащих соответственно пересечение E[ ]∩S_p(x_k) и ∩S_r(x_k), где ν ≥ 0, τ ≥ 0 – параметры семейств. Центр и матрица H_k+1 оценивающего эллипсоида, для которого гарантированно выполняется включение x_k+1Î , определяются соотношениями .Робастный алгоритм построения семейства эллипсоидов  имеет вид

, (20)

,     (21)

.                             (22)

Здесь e_k=h_k^TH_kh_k, , , I_m – единичная матрица размерности m´m, b_kÎ(0,1) и a_k >0 – параметры алгоритма.

Центр  и матрица  эллипсоида É ÉS_r(x_k) вычисляются по формулам (20) – (22) с заменой в их правых частях величин n, H_k, c_p и  соответственно на величины τ, , , c_r и .

Оценивание состояния непрерывных ДС. Для гарантированного эллипсоидального оценивания вектора состояния x_k = x(t_k) системы (8), (9) в дискретные моменты времени t = t_k, соответствующие моменты измерения выхода y_k = y(t_k) и изменения вектора управления u_k = u(t_k), опишем эту систему разностными уравнениями вида (1), (2). Воспользовавшись формулами для решения систем линейных дифференциальных уравнений с переменной матрицей, получаем

A_k = K(t_k+1,t_k), f_k( u_k )=B_ku_k,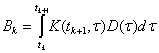

Здесь K(t, t_k) – переходная матрица (матрица Коши) системы (6) при t≥t_k. Матрица K(t_k+1,t_k)=X(t, t_k) при t=t_k+1, где X(t, t_k) – решение дифференциального матричного уравнения с начальным условием X(t_k, t_k)=I_n. Для случая стационарной системы (8)

A_k≡A=exp{CT}, B_k≡B= 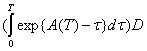[10, 11].

     На данном этапе разработки был проведен анализ текущего состояния экономики, который подтвердил необходимость применения методов математического моделирования. При постоянно меняющейся экономической ситуации и продолжительных кризисах был выбран робастный метод эллипсоидального оценивания состояния динамических систем при ограничениях на помехи измерения выхода и скорость их изменения.

Теоретические данные данной работы могут найти применение в любой сфере экономики и не только для оценивания состояния динамических систем и для оптимального управления ими, а также могут служить стратегией для управления экономикой.

Литература

1. Волосов В.В. Робастные методы эллипсоидального оценивания состояния динамических систем при ограничениях не помехи измерения выхода и скорость их изменения / Волосов В.В. Шевченко В.Н. // Проблемы управления и информатики, 2008, №5, с.85-93

2. Лебедева И.В. Моделирование нелинейных экономических систем с помощью динамических рядов. / Лебедева И.В. // Современные наукоемкие технологии, № 4, 2009.

3. Самарский А.А., Математическое моделирование / Самарский А.А., Михайлов А.П. // Идеи. Методы. Примеры. – 2-е изд., испр. – М.: Физматлит, 2001.