К.ф.-м.н. Долгарев И.А.

Пензенский государственный университет

явно зададанные поверхНости

некоммутивного галилеева пространства-времени с растраном

Евклидово пространство и пространство-время Галилея имеют своей основой соответствующее векторное пространство, строятся в векторной аксиоматике Г. Вейля. Евклидово пространство использует евклидово скалярное произведение векторов, пространство-время Галилея использует галилеево скалярное произведение векторов. Векторы могут быть интерпретированы как параллельные переносы аффинного пространства, составляют коммутативную алгебраическую структуру – линейное пространство над полем, часто выбирается поле действительных чисел. Существуют другие алгебраические структуры аффинных преобразований – одули Ли, на которых в аксиоматике Г. Вейля определены геометрические пространства, см. [1]. Линейное пространство является коммутативным одулем Ли. Выделяется одуль Ли, состоящий из параллельных переносов и гомотетий аффинного пространства и называемый растраном. Относительно композиции преобразований растран является некоммутативной группой. Геометрия пространства с растраном одулярна и некоммутативна, см. [1, c. 136 – 165]. На растране определено галилеево скалярное произведение растов (элементов растрана) и изучается галилеево пространство-время с растраном. Для поверхностей пространства с растраном доказана основная теорема: поверхность однозначно определяется коэффициентами своих первой и второй квадратичных форм, [2].

В частности, поверхность 3-мерного пространства может быть задана явной функцией . В этом случае теория поверхностей более проста, чем при параметрическом задании поверхности, [3, c. 8 – 30]. Установлено, что всякая регулярная поверхность евклидова пространства в окрестности своей обыкновенной точки описывается явной функцией, [4, c. 72 – 73]. В [5] рассматриваются галилеевы квадратичные формы евклидовой поверхности, заданной явной функцией. Ниже изучаются явно заданные поверхности в галилеевом пространстве с растраном, для них доказывается определяемость двумя коэффициентами их квадратичных форм.

1. Галилеево пространство-время с растраном

1.1. Растран

Одули над кольцом определены в [6] Л.В. Сабининым в 1977 году, одули Ли впервые рассмотрены в [1, c. 102 – 112], первые сведения о растране и пространстве с растраном опубликованы в [7]. На многообразии однородный растран задается следующими операциями (;):

, , .

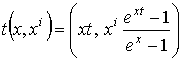См. [1, c. 107]. Элементы растрана называются растами и обозначаются малыми греческими буквами. Пусть , , . Имеется разложение

.

Упорядоченное множество является базисом растрана . Расты составляют подрастран, являющийся 1-мерным линейным пространством ; расты составляют 2-мерное линейное пространство . Растран есть полупрямая сумма линейных пространств = L²┤L¹, подрастран L² является инвариантным в растране .

1.2. Галилеева норма на растране.

Галилеевой нормой ||w|| раста w=(x, x¹, x²) называется

, если x ≠ 0;

, если x = 0.

Линейные пространства и превращаются в евклидовы векторные пространства соответственно и , нормированный растран является полупрямой суммой евклидовых пространств =┤. Составляющая этой суммы – временная, составляющая – пространственная.

Расты (0,x¹,x²) называются евклидовыми, это векторы евклидова пространства , расты , x≠0, называются галилеевыми. Всякий галилеев раст перпендикулярен всякому евклидову расту. [1]. Евклидову расту соответствуют параллельные переносы, галилееву – гомотетии аффинного пространства.

1.3. Дифференцирование растранных функций.

Растранная функция r(t) представляет собой упорядоченную совокупность (x(t), x¹(t), x²(t)) трех действительных функций действительного параметра. Рассматриваем функции класса C ³. Получена следующая формула дифференцирования растранных функций, [1]:

.

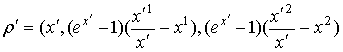Свойства дифференцирования векторных функций на растранные функции не распространяются. Если , то функция r(t) дифференцируется как векторная. Если , то

= .

Для функций частные производные , отыскиваются как производные функций одного параметра. При этом: .

1.4. Определение ЕМ-пространства.

Отображение пар точек множества в нормированный растран , удовлетворяющее аксиомам Г. Вейля, задает на пространство с растраном, называемое ЕМ-пространством. Размерность ЕМ-пространства есть размерность растрана, обозначение . Если в репере B = (0, a, b, g) ЕМ-пространства: A = (a,a¹,a²) и B = (b,b¹,b²), то AB = (b-a, b¹-a¹e^b-a, b²-a²e^b-a). Расстоянием |AB| между точками A и B в ЕМ-пространстве равно норме раста AB. Согласно п. 1.2,

, если b ≠ a;

, если b = a.

ЕМ-пространство является одулярным галилеевым пространством-временем.

1.5. Поверхности ЕМ-пространства.

В ЕМ-пространстве рассматриваем регулярные поверхности класса в естественной параметризации

= , . (1)

Имеем разложение

= + ,

где = векторная функция евклидовой плоскости = ЕМ-пространства, [1]. Это также векторное поле евклидовой плоскости, евклидова проекция поверхности на плоскость . Слагаемое есть временная составляющая поверхности, параметр – время, – пространственная составляющая поверхности.

На основании формул дифференцирования растранных функций, п. 1.3, имеем следующие частные производные первого порядка функции :

= = , = = (1, (e-1), (e-1));

Производные второго порядка растранной функции таковы:

= , = , .

1.6. Квадратичные формы поверхностей ЕМ-пространства.

По [1], первая квадратичная форма поверхности (1) r(u,t) есть

или , (2)

Вторая квадратичная форма поверхности:

ее коэффициенты

, , ; (3)

единичный вектор нормали поверхности равен

, . (4)

Как евклидов раст, вектор перпендикулярен всякой линии на поверхности, проходящей через рассматриваемую точку поверхности. Нормальная кривизна линий на поверхности вычисляется по формуле

,

– направление на поверхности.

1.7. Основная теорема теории поверхностей

Для поверхностей ЕМ-пространстства-времени выполняются аналоги формул Петерсона-Кодацци

, , (5)

см. [1, c. 156 – 158]. По вычислительным формулам (2) и (3) коэффициентов первой и второй квадратичных форм поверхности некоммутативного пространства-времени с растраном, при использовании (4), составлена система дифференциальных уравнений с частными производными:

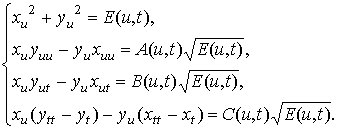(6)

Функции

E = E(u,t) ³ 0, A = A(u,t), B = B(u,t), C = C(u,t) (7)

заданы, отыскиваем функции – компоненты растранной функции , задающей поверхность в ЕМ-пространстве. В [2] доказана основная теорема теории поверхностей ЕМ-пространства

ТЕОРЕМА. Если на односвязной области D евклидовой плоскости ЕМ-пространства М³ заданы функции (7) класса C³ , для которых выполняются условия в виде формул Петерсона-Кодацци, то на области D определяется функция , пространственная составляющая поверхности (1) в ЕМ-пространстве , имеющая коэффициенты (7) первой и второй квадратичных форм. Существует единственная поверхность , удовлетворяющая условиям

, , , , (8)

где , , , заданные векторы, и не коллинеарны.

2. Явно заданные поверхности ЕМ-пространства

2.1. Явное задание поверхности

В ЕМ-пространстве изучаются регулярные поверхности (1) в естественной параметризации. Условия регулярности поверхности таковы, что они являются условиями обратимости функции в задании (1), в случае, если это не постоянная величина. Эти условия подробно обсуждаются в [4, c. 72 – 73]; функция евклидова. Таким образом, в окрестности обыкновенной точки поверхности (1) поверхность может быть задана функцией

.

Следовательно, имеем параметрическое задание поверхности

= . (9)

2.2. Коэффициенты квадратичных форм поверхности

Пространственная составляющая поверхности (9) такова

.

По формулам в конце п. 1.5. находим производные функции :

, =,

производные второго порядка равны

,

, .

Коэффициент первой квадратичной формы поверхности (9) есть

, ;

откуда

. (10)

Согласно (4), имеем единичный раст нормали поверхности (9)

.

Находим коэффициенты второй квадратичной формы поверхности по (3):

, , .

Из первых двух равенств с использованием (10) выражаем коэффициенты и второй квадратичной формы поверхности через коэффициент первой квадратичной формы:

, ; .

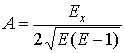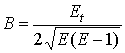Осталось два коэффициента и , по которым можно пытаться найти поверхность. На их основе получаем систему дифференциальных уравнений с частными производными

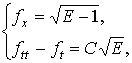(11)

к которой сводится система уравнений (6) в рассматриваемом случае. По основной теореме для поверхностей ЕМ-пространства, п. 1.7, функция является решением системы (11) если заданы функции

E = E(x,t) ³ 0, C = C(x,t).

Эти функции удовлетворяют второй из формул Петерсона-Кодацци в (5). Единственная поверхность определяется начальными условиями (8)

, , , ,

где , , , заданные векторы, и не коллинеарны.

2.3. Отыскание функции

Интегрируя первое уравнение системы (11) по параметру и учитывая, что в результате может получиться функция, зависящая от параметра , имеем:

.

Подставляя найденную функцию во второе уравнение системы (11), отыскиваем функцию . Начальные условия (8) выделяют единственную поверхность с заданными коэффициентами и квадратичных форм поверхности. Система (11) дифференциальных уравнений с частными производными проще системы (6).

2.4. Пример нахождения поверхности по двум коэффициентам и

Пусть , 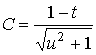. Второе равенство из (5) выполняется. По (10), =; по третьей из формул в (3), . Система уравнений (11) имеет вид

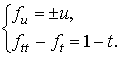(12)

По первому уравнению в (12) получаем 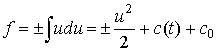. Согласно второму уравнению в (12): . Решение уравнения есть: ; частное решение уравнения имеет вид , некоторые числа. Находим и . Начальные условия =, , , выделяют поверхности =.

Литература

1. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005. - 306с.

2. Долгарев И.А. Получение поверхности 3-мерного галилеева про-странства с растраном по коэффициентам ее квадратичных форм. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, – Пенза: 2007, № 6(33), С. 17 – 31.

3. Розендорн Э.Р. Теория поверхностей. Изд. 2. М.: Физматлит, 2006.

304с.

4. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. М.: Наука – 1979, 760с.

5. Долгарев И.А. Галилеевы квадратичные формы евклидовой поверхности.// Метрическая геометрия поверхностей и многогранников. Междунар. Конф., посв. 100-летию со дня рождения Н.В. Ефимова. Москва, 18 – 21 авг. 2010. Сборник тезисов. М.: МАКС Пресс, 2010. - С. 24 – 25.

6. Сабинин Л.В. Одули как новый подход к геометрии со связностью// ДАН СССР. 1977. № 5.- С. 800 – 803.

7. Долгарев А.И. ЛМ-пространства. //Римановы пространства и мето-ды эллиптических дифференциальных уравнений. Л.: ЛГПИ, 1986. - С.8-25.