ФИЗИКА/ 2.Физика твердого тела.

Ильюшин Ю. В.

Пятигорский государственный гуманитарно-технологический университет, Россия

Синтез управляющих воздействий на основе импульсных переходных функции

Типовое линейное уравнение второго порядка, моделирующее поведение функции состояния пространственно одномерного объекта с распределёнными параметрами может быть представлено в форме:

; ; ;

с начальными и граничными условиями:

; ; ;

, ;

, .

В роли входных воздействий кроме функций могут фигурировать соответствующие управления .

Граничные управления для одномерного объекта, сконцентрированные в точках и на границах отрезка, представляют собой сосредоточенные воздействия, изменяющиеся только во времени . Управления могут представлять собой как независимые от пространственных координат управления (сосредоточенные), так и пространственно-временные воздействия.

Основное соотношение, связывающее выход объекта при заданном начальном состоянии с входными воздействиями, определяется общим решением краевой задачи, которое может быть представлено в следующей интегральной форме:

, ;

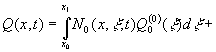
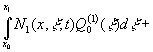
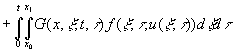
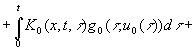
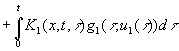где и переменные интегрирования, соответственно, по пространственной координате и времени. Первые два интеграла по пространственной переменной определяют составляющую общего решения, описывающую влияние на начальных распределений и . Последние два интеграла по времени учитывают сосредоточенные входные воздействия и по граничным условиям. Двойной интеграл по пространственно-временной области изменения пространственного и временного аргументов распределённого входного воздействия отражает его вклад в реакцию объекта. Выход объекта связывается с внешними воздействиями ,, и начальным состоянием соответствующими ядрами линейных интегральных операторов , отражающими внутренние свойства объекта по отношению к соответствующим входам. Как следует из общей теории линейных уравнений в частных производных, все эти ядра могут быть выражены в конечном виде только через одну из них – функцию , называемую функцией Грина, которая является основной фундаментальной характеристикой объекта.

Если в краевой задаче начальные условия нулевые, а граничные условия однородные, то есть , , и функция представляется произведением дельта-функций: , то в соответствии со свойствами дельта-функций, получим:

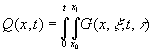
Таким образом, функция Грина является решением краевой задачи:

; ; ;

; ;

, ;

, .

и описывает реакцию управляемой распределённой системы с нулевыми начальными и однородными граничными условиями в любой точке и любой момент времени на точечное импульсное воздействие вида дельта-функции, приложенное в произвольной, но фиксированной точке в момент времени .

В общем вход-выходном соотношении функция Грина представляет собой реакцию объекта в точке в момент времени при нулевых начальных и однородных граничных условиях на импульсное воздействие, приложенное в каждой точке в каждый момент времени .

Если параметры распределённого объекта не зависят от времени, то соответствующий ему распределённый блок называют стационарным. Импульсная переходная функция такого блока может быть записана в виде:

.

В случаях, когда нельзя ограничиться уравнениями объекта в вариациях, необходимо непосредственно учитывать нелинейности в структуре соответствующих нелинейных блоков. В достаточно общем случае соотношение между выходом и входом для нелинейного блока принимает вид следующего нелинейного интегрального оператора:

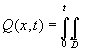
с ядром , являющимся заданной нелинейной функцией входного воздействия . В получено интегральное уравнение относительно функции состояния нелинейного объекта в форме:

;

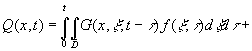
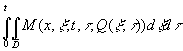где .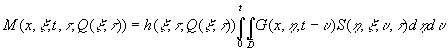

Синтез программных управлений тепловыми процессами

В модальном представлении аналитические решения представляют собой бесконечные или конечные линейные комбинации «мод» как совокупности экспоненциально-периодических базисных функций времени и координат. По аналогии с сосредоточенными объектами для задачи температурной стабилизации распределённых объектов возможно использование классических законов теории управления, в соответствии с которыми управляющие воздействия могут формироваться как функции отклонений температуры от заданной. Задачи синтеза программных управлений рассмотрены в работе.

Синтез программных управлений осуществляется на основе моделей процессов в распределённых объектах путём формализации требований к процессам в виде одноточечных или многоточечных целевых условий типа равенств, неравенств или условий представленных требованиями минимизации функционалов качества. Для связи между управляемыми координатами и управляющими факторами используются аналитические решения операторов теплопроводности или разностные схемы для соответствующих задач. Это позволяет получить большое разнообразие алгоритмов программного управления, которые при соответствующем обобщении могут служить основой для создания систем локально-оптимального или локально-целевого управления. Подход к синтезу локально-оптимального управления для тепловых процессов может базироваться на задачах теплопроводности с использованием разностных схем. Разностные схемы позволяют «алгебраизовать» оптимизационные задачи синтеза управлений и свести их к решению счётного числа конечномерных задач математического программирования. Задачи математического программирования должны решаться на каждом шаге процесса управления с применением операторов конечномерной оптимизации.

Подходы к синтезу стабилизирующих управлений для распределённых объектов могут быть обобщены системным обобщением методов на основе вариантных целевых условий и разрешением задач математического программирования численными методами. В результате разрешения целевых условий необходимо получить явное представление законов обратных связей и исследовать условия устойчивости замкнутых систем стабилизации распределённых объектов.

Целевые условия типа равенств задают требования по обеспечению заданных значений координат в заданные моменты времени, что позволяет свести задачу к решению системы алгебраических уравнений относительно параметров объекта или внешних возмущений.

Если аналитическое решение начально-краевой задачи, то система целевых равенств имеет вид:

;

где заданное значение температуры в фиксированные моменты времени. Поскольку аналитическое решение определено с точностью до параметров нагреваемого тела и внешних возмущений, то система может быть разрешена относительно последних переменных.

Целевые условия типа неравенств формируются по аналогии с условиями. Они определяют интервальные требования к координатам объекта для совокупности заданных моментов времени. Задача сводится к решению конечного числа систем неравенств:

,

заданных относительно параметров объекта или параметров входных воздействий.

Целевые условия в виде минимизации функционала, определённого на отклонениях теплового режима от заданных требований реализуются минимизацией параметров объекта или входных воздействий. Это позволит свести задачу синтеза к задачам конечномерной минимизации:

,

где и аналитические значения температуры в заданные моменты времени и координат и их численные значения.

Рассмотрим пример. Пусть имеется уравнение распространения тепла в изотропном стержне:

,

с начальными и граничными условиями:

; .

Требуется найти параметры решения , которые выбираются из условия удовлетворения заданным начальным условиям типа равенств, неравенств или условиям, представленным в виде требования минимизации некоторого функционала качества. Синтез проводится с использованием аналитических решений начально-краевых задач. Для представления обобщённого решения можно использовать формальный ряд :

.

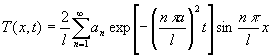При использовании одноточечного условия по времени и по координатам задача сводится к решению равенства относительно параметров:

.

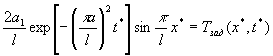Равенство представляет собой нелинейное алгебраическое уравнение относительно параметров, которые обеспечивают выполнение целевых условий.

В случае многоточечных целевых условий типа, задающих тепловые режимы объекта на семействах точек временной и координатной осях, можно свести задачу синтеза к задаче решения системы уравнений относительно параметров:

.

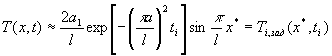При использовании ряда с конечным числом слагаемых задача преобразуется к системе уравнений:

.

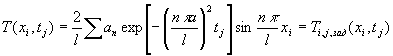Используя данную функцию можно решать задачи измерения температурных полей на пространственно распределенных объектах.

Список литературы

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972. – 736 с.

2.Чернышев А.Б. Исследование нелинейных распределённых систем управления температурными полями. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. Спец. выпуск Математическое моделирование и компьютерные технологии. – Новочеркасск, 2004. – С. 57-60.

3. Першин И.М. Анализ и синтез систем с распределенными параметрами. – Пятигорск: Изд-во РИА-КМВ, 2007. – 244 с.

4. Ильюшин Ю. В. Стабилизация температурного поля туннельных печей конвейерного типа. Научно технические ведомости СПбГПУ. -2011.-№ 3(126). С 67-72.

5. Чернышев А.Б. Ильюшин Ю.В. Определение шага дискретизации для расчета теплового поля трехмерного объекта управления // Изв. Южного федерального университета № 6.-Таганрог, 2011. С 192-200.

6. Чернышев А.Б. Ильюшин Ю.В. Устойчивость распределенных систем с дискретными управляющими воздействиями // Изв. Южного федерального университета № 12. - Таганрог, 2010. С 166-171.

7. Душин С.Е., Зотов Н.С., Имаев Д.Х. и др. Теория автоматического управления. //Под ред. В.Б. Яковлева. – М.: Высшая школа, 2003. – 567 с.

8. Чернышев А.Б., Антонов В.Ф., Шураков Д.Л. Система стабилизации температурного поля в процессе утилизации тепла при контактной сварке.// Научно-технические ведомости СПбГПУ. – 2010. – № 6(113). – С. 151-155.

9. Чернышев А.Б. Модификация критерия абсолютной устойчивости для систем с распределенными параметрами. Ставрополь: СевКавГТУ, 2008.

10. Рапопорт Э.Я. Структурное моделирование объектов и систем управления с распределенными параметрами. М.: Высшая школа, 2003.

11. Першин И.М. Анализ и синтез систем с распределенными параметрами. Пятигорск: РИА-КМВ, 2007.

12. Першин И.М. Синтез систем с распределенными параметрами. Пятигорск: РИА-КМВ, 2002.