Технические науки/2. Механика

Гавеля Г.М.

Днепропетровский национальный университет им. О Гончара, Украина

ИДЕНТИФИКАЦИЯ ТОЛЩИНЫ ТОНКОСТЕННОЙ ОБОЛОЧКИ

Тонкостенные оболочки находят широкое применение в качестве несущих и защитных элементов в ракетостроении, атомных реакторах, кораблестроении, металлургии. Диагностика реального состояния тонкостенных конструкций в процессе эксплуатации весьма актуальна. Процесс мониторинга таких конструкций, обычно связанный с измерением перемещений, весьма затруднен, обусловленность такой задачи диагностики весьма низка. Поэтому разработка таких математических моделей и методов идентификации отклонений в номинальных параметрах тонкостенных конструкций, в частности, толщины (ее изменение образуется в процессе изготовления или эксплуатации), даст возможность повысить надежность их эксплуатации.

В данной работе рассматривается задача об определении функции распределения толщины по поверхности оболочки по результатам наблюдений. В качестве наблюдаемых параметров выступают значения функций , характеризующих напряженно-деформированное состояние (НДС) в точках измерений; главной особенностью таких обратных задач является некорректность [1]. Поэтому для решения поставленной задачи должен быть использован метод регуляризации [4], в качестве которого может быть использован прием выбора решения на множестве корректности, тогда задача определения неизвестной толщины может быть сформулирована как

, (1)

где − наблюдаемые значения функций НДС, − множество корректности (компакт), − множество возможных состояний оболочки, − метрика в пространстве состояний, которая должна быть задана на основе учета свойств решений прямой задачи [4], − функция, характеризующая распределение толщины.

Для поиска решения из соотношения (1) при известном решении прямой задачи может быть использована нейросетевая аппроксимация, если принять, что , – вектор входных значений нейросети, , – вектор её выходных значений [2,3]. Поведение тонкостенной оболочки переменной толщины в ограниченной пространственной области , где − вектор пространственных координат, описывается соотношениями:

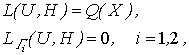(2)

где − вектор-функция перемещений, − граничные контуры области , − заданные дифференциальные операторы, − внешнее воздействие. В качестве математической модели обратной задачи выбрана нейросетевая аппроксимация; в случае использования двухслойного персептрона имеем

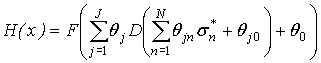, (3)

где – активационные функции, – число нейронов в слоях; – вектор настраиваемых параметров; – значения заданных функций в фиксированных точках области .

Для получения решения из уравнений (2) и использования его в структурной схеме обучения сети (3) используется метод конечных элементов. Для аппроксимации всех функций задачи вводятся следующие сетки:

1) для решения прямой задачи НДС тонкостенной оболочки вводится сетка с координатами узлов , где , и соответствующими значениями для функции ,;

2) для структурирования информации о наблюдаемых значений функции вводится сетка с координатами узлов , , , и значениями , ;

3) для описания функции толщины вводится сетка , , , с соответствующими значениями функции , .

Для решения задачи (2) используется аппроксимация на элементе в виде:

, (4)

где – матрица функций формы; – вектор узловых значений функции перемещений.

После выполнения процедуры метода Бубнова-Галеркина для задачи (2) с учетом аппроксимации (4) и суммирования матриц элементов можно получить систему линейных алгебраических уравнений

, (5)

где – матрица жесткости, – вектор внешней нагрузки.

Предложенный подход был реализован для идентификации толщины цилиндрической оболочки, находящейся под действием внешнего равномерно распределенного давления. Геометрические и физические параметры оболочки: радиус , длина , толщина , модуль упругости , коэффициент Пуассона .

В качестве обучающей выборки использовались различные варианты расположения областей изменения толщины с соответствующими наблюдаемыми прогибами, в качестве нейронной сети – двухслойный персептрон. Участок разнотолщинности располагался в диапазоне , , где – координаты центра тяжести участка утонения (утолщения). Изменение значений проводилось на координатной сетке , т.к. граница области разнотолщинности совпадала с границей элементов сетки . Толщина изменялась в диапазоне значений , где , .

В таблице приведены результаты прогноза значений толщины по результатам наблюдений, в качестве которых использовались значения перемещений, определенные из тестовых прямых расчетов, не входящих в выборку.

Таблица. Прогноз значений толщины по результатам наблюдений

Область	Координаты центра области				( %)
1	2.355	2.25	0.07713	0.07559	2
	2.355	2.25	0.06856	0.06650	3
	2.355	2.25	0.05999	0.05849	2.5
2	7.065	6.75	0.07713	0.07481	3
	7.065	6.75	0.06856	0.06684	2.5
	7.065	6.75	0.05999	0.05867	2.2
3	11.775	11.25	0.07713	0.07535	2.3
	11.775	11.25	0.06856	0.06664	2.8
	11.775	11.25	0.05999	0.05819	3

Из таблицы видно, что применение предложенного алгоритма идентификации толщины дает достаточные по точности результаты. Предложенный алгоритм может быть использован в соединении с результатами мониторинга для идентификации толщины оболочки в реальных элементах систем при их эксплуатации.

Литература:

1. Ватульян А. О. Обратные задачи в механике деформируемого твердого тела – М.: Физматлит, 2006. – 222 с.

2. Гук Н.А., Ободан Н.И., Гавеля Г.М. Выбор критерия идентификации в обратных задачах теории оболочек // Проблеми обчислювальної механіки і міцності конструкцій. – Д.: Наука і освіта, 2010.–Вип..14.–С.123 – 133.

3. Ободан Н.И., Рундуев К.В. Восстановление нагрузок, действующих на наблюдаемые тонкостенные системы, с помощью ядерных нейронных систем // Проблеми обчислювальної механіки і міцності конструкцій. – Д.: Наука і освіта, 2010.–Вип..14.–С.267 – 277.

4. Тихонов А. Н., Арсенин В.Я. Методы решения некорректных задач – М.: Наука, 1986. – 286 с.