Рябоштан А.Ф., Миленин А.Н.

Харьковский национальный технический университет сельского хозяйства им. П. Василенко

Математика/4.Прикладная математика

Конструирование порций поверхности дискретной сетью специальных линий

С практической точки зрения важным является определение сети специальных линий с заданными параметрами на сконструированной поверхности. Тем более важной является задача формирования и аналитического описания поверхности, у которой заданные линии или их сеть являлись бы специальными линиями будущей поверхности. Конструирование таких линий используется при проектировании поверхностей лопаток газовых турбин, различных оболочек, лемешно-отвальных поверхностей и т.п. При этом используется два важных свойства этих линий – совпадение ее главной нормали с нормалью поверхности и ее свойство быть кратчайшей линией поверхности.

Подобные задачи возможно решать при помощи дифференциальных уравнений с частными производными I порядка. Однако формирование поверхности по заданной сети и ее специальных линий оказывается возможным только при наличии уравнения четырехугольной порции поверхности I порядка гладкости. Значения функций оснащения в узлах порций поверхности должны быть согласованными.

Пусть ребра порции поверхности заданы уравнениями - параметрическое уравнение кривой для координат соответственно

Бинормаль кривой имеет координаты

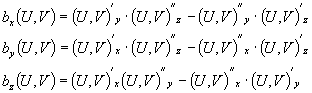(1)

где штрихи означают производные по параметру. Главная нормаль кривой имеет координаты

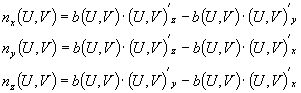(2)

Две линии будут ассимптотичными линиями поверхности, если определяемая ими в точке пересечения нормаль поверхности будет бинормалью каждой из кривых. Для этого достаточно соблюдения двух равенств

; (3)

Последовательной стыковкой порций поверхности можно получить произвольную лоскутную поверхность, заданную дискретной сетью линий.

Путь задано - параметрическое множество линий

; , . (4)

Поверхность конструируется из множества линий наложением связей на параметр ; при помощи начальных условий, в качестве которых выступают:

1. кривая, с которой линии пересекаются;

2. поверхность, с которой линии имеют касание I или II порядков.

Рассмотрим эти условия.

1. Кривая :

, ; . (5)

Из условия пересечения с кривыми множества при подстановке (5) в (4) позволяет получить два уравнения связи параметров

, , (6)

где общее количество параметров увеличилось на 1 (прибавился ), а общее количество уравнений на 2, т.к. из уравнений (6) можно получить уравнения связи параметров

, , (7)

обеспечивающее пересечение кривых множества с кривой . Для получения поверхности из (4) необходимо иметь таких связей и, следовательно, начальных кривых в виде (5).

2. Пусть в качестве начального условия задана поверхность

. (8)

Условие перпендикулярности касательных к линиям (4) и нормалей к поверхности (8) дает дифференциальное уравнение:

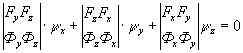(9)

где , , - частные производные функции .

Если из системы уравнений (4), (8), (9) исключить координаты точки касания, получим одно уравнение связи параметров

. (10)

Следовательно, для получения поверхности из множества (4) при соблюдении касания I порядка к заданным поверхностям необходимо иметь в качестве начальных условий уравнений (9), что совместно с (4) дает уравнений, из которых нужно исключить параметров. Для обеспечения второго порядка гладкости соприкосновения заданной поверхности (8) к искомой необходимо вычислить частные производные по формулам

, ,

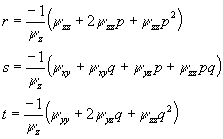(11)

подставить их в уравнение (5), общее для множества поверхностей, полученных из линий (4).

Совместное рассмотрение уравнений (4) и (8) и полученного уравнения после исключения , и дает уравнение связи параметров

. (12)

Уравнения (10) и (12) гарантируют соприкосновение второго порядка гладкости. Указанное условие равносильно фиксированию двух параметров на границах порций поверхности при проектировании лопаток газовых турбин.