Экономические науки/8. Математические методы в экономике

Садыков В. М., Матяж Н. В.

Автомобильно-дорожный институт ГВУЗ ДонНТУ

Теория катастроф и моделирование экономических процессов

На данном этапе развития цивилизации можно выделить ряд основных факторов, способных привести к глобальным катастрофам (в математическом понимании) с отрицательными и положительными последствиями. Такими катастрофами являются демографический взрыв, энергетический, экологический, сырьевой кризисы, международные конфликты, социально-экономические и научные кризисные ситуации, увеличение разрыва в уровне жизни между различными слоями населения одной страны, между экономически развитыми и развивающимися странами, возможность резкого скачка в развитии отдельной страны и многие другие явления и процессы.

В последнее время активно стали появляться публикации по проблеме катастроф в экономике, которые, как правило, посвящаются констатации неблагоприятных событий в той или иной сфере человеческой деятельности и возможному анализу причин и последствий (труды П.Т. Обыденного, В.Л. Владимирова).

В кризисной ситуации, которую переживает современный мир, достоверное, конкретное знание все же лучше любой неопределенности [1]. Научный поиск идет в основном в направлении создания математических моделей развития процессов на глобальном уровне, а также вопросов, связанных с развитием систем. Любая система претерпевает кризисные этапы, характеризующиеся временным преобладанием одной из сил, что приводит к хаосу, разрушающему предыдущие структуры; затем происходит гармонизация, равновесие восстанавливается, но уже в новом, качественно ином состоянии [2].

Следовательно, необходимо акцентировать внимание на проблеме обоснования использования основных положений теории катастроф для глобального и локального моделирования экономических процессов.

Термин «катастрофа» был введен в конце 60-х годов для обозначения качественного изменения объекта при плавном изменении параметров, от которых объект зависит. Математическим базисом теории катастроф является теория особенностей гладких отображений – обобщение исследования функции на наличие экстремумов. Последние представляют собой критические точки функции, которые во многом определяют ее поведение.

Классификационной теоремой Тома [3] доказано, что если число параметров не превышает четырех, то существует лишь семь типов структурных неустойчивостей, названных элементарными катастрофами (число К_Э), независимо от числа фазовых переменных. В настоящее время в большинстве предлагаемых моделей используется лишь одна фазовая переменная [4]. В этом случае К_Э = 4, а любая система может рассматриваться как градиентная.

Простейшая элементарная катастрофа (с одним параметром с) называется «складка», и для нее потенциал F в дифференциальном уравнении 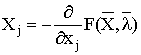, имеет вид .

Катастрофа с двумя параметрами (а, b) называется «сборка». Она имеет функцию . Именно она получила наиболее широкое распространение в приложениях. Согласно классификационной теореме любая гладкая функция имеет особенности только типа «складки» и «сборки».

Отложив в трехмерном пространстве по вертикальной оси значения х действительных стационарных точек, а по двум другим осям – значения параметров (а, b), получим некоторую поверхность. В точках перегиба поверхности, имеющих вертикальную касательную, происходит слияние двух стационарных режимов, соответствующих минимуму и максимуму . Их проекции на плоскость параметров (а, b) дают бифуркационную кривую.

Параметр (а) получил название нормального фактора, параметр (b) – расщепляющего фактора, который называется так потому, что при b > 0 поверхность поведения расщепляется на два листа.

Таким образом, одной из главных проблем при построении модели является выделение пары основных факторов (а, b), изменение которых определяет скачкообразные переходы в данном процессе.

Пусть функция характеризует состояние экономики в зависимости от какого-либо параметра. Если экономика регулируется так, чтобы обеспечивать максимизацию функции, то система будет находиться в точке максимума А. Если при изменении дополнительного параметра максимум А (локальный экстремум) исчезает, то система скачкообразно перейдет в состояние В (рис. 1). Такого рода скачки получили название катастроф, так как они связаны с резкими изменениями в состоянии системы и могут приводить к ее разрушению.

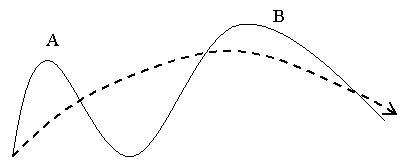
Рисунок 1 – Качественное представление понятия «катастрофа»

В. И. Арнольд [5], считает, что картина вблизи рассматриваемого локального экстремума могла быть примерно такой:

- вначале оптимальное решение единственно;

- по мере развития системы вместе с близким локальным минимумом возникает новый локальный максимум;

- с момента, когда побочный максимум обгоняет исходный, новый режим становится выгоднее старого. Но переход на него затруднен необходимостью резкого скачка – катастрофы.

Поэтому при плавном переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.

В линейных системах малые изменения параметра в сторону лучшего режима улучшает положение, но после достижения локального экстремума такие же изменения управляющего параметра не улучшают, а ухудшают положение. И поскольку система стремиться оптимизировать свое состояние, то она будет отвечать на недостаточно радикальные изменения возникновением сильных тенденций возврата к старому режиму.

Наконец, в ходе дальнейшего развития системы исходное локально-оптимальное состояние вообще исчезает и переход на далекий от первоначального режим становиться неизбежным.

Таким образом, в момент катастрофы оба режима сближаются с бесконечной скоростью. Это объясняет, почему с почти наступившей катастрофой бороться очень сложно.

Модели, использующие катастрофу типа «сборки», описывают самые разнообразные процессы. Они достаточно просты и удовлетворяют представлениям о скачкообразном переходе как результате взаимодействия противодействующих (в простейшем случае двух) факторов.

При использовании для построения моделей различных процессов катастрофы типа «сборка» общим является то, что пока значение фактора b мало, изменение системы х в зависимости от а происходит медленно и непрерывно, а когда b - велико, наблюдается резкий скачок.

Таким образом, одно из главных значений теории катастроф в науке состоит в том, что она сводит огромное многообразие практических ситуаций к небольшому числу стандартных моделей, поведение которых можно детально исследовать.

Развитие любой системы представляет собой процесс прохождения ряда неустойчивых моментов (точек) и исследование поведения систем в этих точках представляется очень важным.

Неустойчивость в экономических системах проявляется в различных критических ситуациях, которые возникают при изменении соответствующих параметров в результате влияния среды, экономических изменений, научно-технического прогресса и др. Эти критические ситуации играют существенную роль в изменении состояния экономических систем, поэтому так важен их анализ, который осуществляется через соответствующее моделирование.

Выяснение подобных критических границ, на которые выходит человечество в настоящее время, является, в частности, задачей нового направления исследований общественного развития - глобального моделирования.

Поводом для использования теории катастроф в области глобального моделирования являются такие свойства экономического развития как увеличение разрыва в жизненном уровне между экономически развитыми и развивающимися странами (дивергенция), возможность резкого изменения (скачка) в уровне развития отдельной страны и др. Эти свойства дали основание использовать катастрофу «сборка» для качественного анализа глобальной модели.

Начальные попытки использования теории катастроф для моделирования экономических кризисных ситуаций глобального развития носят несколько упрощенный характер и не отражают всей сложности анализируемой проблемы, нуждаются в проведении обширных эконометрических и социометрических исследований, а также исследований уже имевших место критических ситуаций. Для прогнозирования изменений экономической системы, находящейся в установившемся устойчивом состоянии, которое признано плохим, поскольку в пределах видимости имеется лучшее, более предпочтительное устойчивое состояние системы, необходимо понять несколько простейших качественных выводов из теории катастроф применительно к нелинейной системе.

Постепенное движение в сторону лучшего состояния сразу же приводит к ухудшению. Скорость ухудшения при равномерном движении к лучшему состоянию увеличивается. По мере движения от худшего состояния к лучшему сопротивление системы изменению ее состояния растет.

Максимум сопротивления достигается раньше, чем самое плохое состояние, через которое нужно пройти для достижения лучшего состояния. После прохождения максимума сопротивления состояние продолжает ухудшаться.

По мере приближения к самому плохому состоянию на пути перестройки сопротивление, начиная с некоторого момента, начинает уменьшаться, и как только самое плохое состояние пройдено, не только полностью исчезает сопротивление, но система начинает притягиваться к лучшему состоянию.

Величина ухудшения, необходимого для перехода в лучшее состояние, сравнима с финальным улучшением и увеличивается по мере совершенствования системы. Слабо развитая система может перейти в лучшее состояние почти без предварительного ухудшения, в то время как развитая система, в силу своей устойчивости, на такое постепенное, непрерывное улучшение неспособна.

В том случае если систему удается сразу, скачком, а не непрерывно, перевести из плохого устойчивого состояния достаточно близко к хорошему, то дальше она сама собой будет эволюционировать в сторону хорошего состояния.

Таким образом, пользуясь вышеописанными качественными выводами, зная состояние самой системы, степень влияния нормального и расщепляющего фактора, можно спрогнозировать практически любое качественное изменение системы. Но в связи с тем, что при анализе подобных систем возможно учесть далеко не все факторы, влияющие на их «поведение», прогнозы, получаемые в результате, будут достаточно условны. На практике невозможно предусмотреть все особенности деструктивных процессов.

Теория катастроф может быть использована для анализа и управления теми или иными экономическими процессами, происходящими в Украине в настоящее время.

ЛИТЕРАТУРА

1. Ерохина Е.А. Теория экономического развития: системно-синергетический подход — Томск: Изд-во Томского ун-та, 1999. — 160 с.

2. Чуличков А. Теория катастроф и развитие мира // Наука и жизнь. 2001. №6.

3. Томпсон Дж.М.Т. Неустойчивости и катастрофы в науке и технике.- М.: Мир, 1985.- 254 с.

4. Постон, Т. Теория катастроф и ее приложения / Т. Постон, И. Стюарт; пер. с англ. – М.: Мир, 1980. – 608 с.

5. Арнольд В. И. Теория катастроф /В. И. Арнольд. - 4-е изд., стер. - М.: Едиториал УРСС, 2004. - 127 с.