Современные информационные технологии/1.Компьютерная инженерия

К.т.н. Ткаченко В.Г., аспирант Кокорев А.В.

Одесская национальная академия связи

Исследование монотонных булевых функций

с малым количеством переменных

В настоящее время значительно расширилась сфера применения цифровых схем. В области телекоммуникаций эти схемы широко используются при сжатии и кодировании передаваемой информации, при цифровой коммутации, в маршрутизаторах и шлюзах. В связи с этим возникает проблема синтеза надежных цифровых схем. В частности это могут быть цифровые схемы, построенные на основе монотонных булевых функций (МБФ). Такие схемы являются более надежными [1], чем схемы, построенные на основе всех булевых функций.

В [2,3] разработана классификация МБФ на типы и перечисление максимальных типов МБФ. Здесь же показано, что для синтеза цифровых схем на основе МБФ необходимо сначала перебрать типы, а затем исследовать все МБФ, принадлежащие определенному типу. В [4] доказано выражение о перечислении типов МБФ в виде произведения матриц.

Покажем на примере простых МБФ, с количеством переменных не более 3, классификацию и исследование этих функций.

Вектор P = (a_n,…, a_i,…, a₁, a₀), компоненты которого принимают значения из множества {0,1}, будем называть входным набором булевой функции от n переменных. Множество всех таких входных наборов образует булев куб [3] ранга n. Сами входные наборы P являются вершинами булева куба. Любую булеву функцию можем определить множеством вершин булева куба, на которых эта функция равна единицы. Любое множество несравнимых вершин булева куба называется антицепью. Для задания МБФ достаточно указать некоторую антицепь в булевом кубе.

Будем говорить, что две МБФ от n переменных принадлежат одному типу, если соответствующие этим МБФ антицепи для любого i от 0 до n содержат одинаковое число наборов с i единицами. В этом случае для каждого i в минимальных дизъюнктивных формах [1] этих МБФ содержится одинаковое число конъюнкций, в которые входят i переменных. В [2] определен тип МБФ, как вектор Т=(a₀, a₁,…,a_i,…,a_n) из n+1-й компоненты, которые нумеруются слева направо от 0 до n, причем i-я компонента вектора a_i равна числу входных наборов данной МБФ, содержащих по i единиц. Число n называется рангом типа Т, число v ненулевых компонент – весом типа Т, номер i первой слева ненулевой компоненты – левой границей типа Т, номер j первой справа ненулевой компоненты – правой границей типа Т, сумму m всех компонент типа Т – мощностью типа Т. Тип Т называется максимальным, если при увеличении любой компоненты соответствующего ему вектора на 1, полученный вектор не соответствует никакому типу.

Имеется всего две МБФ ранга 0. Это f₀(0) тождественно равная 0 и f₁(0) тождественно равная 1. Первая имеет тип (0), а вторая (1). Максимальным является только тип (1).

Имеется три МБФ ранга 1. Это f₀(1) тождественно равная 0, f₁(1) тождественно равная 1 и f₂(1) = x₁. Первая имеет тип (0,0), а вторая (1,0), а третья (0,1). Максимальными являются только два последних типа.

Имеется шесть МБФ ранга 2. Это f₀(2) тождественно равная 0, f₁(2) тождественно равная 1, f₂(2) = x₁, f₃(2) = x₂, f₄(2) = x₁x₂ и f₅(2) = x₁ x₂. Эти МБФ имеют типы (0,0,0), (1,0,0), (0,1,0), (0,1,0), (0,0,1) и (0,2,0) соответственно. Тип (0,1,0) имеют 2 МБФ. Максимальными являются типы (1,0,0), (0,0,1) и (0,2,0).

Имеется двадцать МБФ ранга 3. Это f₀(3) тождественно равная 0, f₁(3) тождественно равная 1, f₂(3) = x₁, f₃(3) = x₂, f₄(3) = x₃, f₅(3) =x₁x₂, f₆(3) = x₁x₃, f₇(3) = x₂x₃, f₈(3) =x₁x₂, f₉(3) = x₁x₃, f₁₀(3) = x₂x₃, f₁₁(3) = x₁x₂x₁x₃, f₁₂(3) = x₁x₂x₂x₃, f₁₃(3) = x₁x₃x₂x₃, f₁₄(3) = x₁x₂x₃, f₁₅(3) = x₁x₂ x₁x₃x₂x₃, f₁₆(3) = x₁x₂x₃, f₁₇(3) = x₁x₂x₃, f₁₈(3) = x₂x₁x₃ и f₁₉(3) = x₃x₁x₂. МБФ f₀(3), f₁(3), f₁₄(3), f₁₅(3) и f₁₆(3) имеют типы (0,0,0,0), (1,0,0,0), (0,3,0,0), (0,0,3,0), и (0,0,0,1) соответственно. Тип (0,1,0,0) имеют МБФ f₂(3), f₃(3) и f₄(3). Тип (0,0,1,0) имеют МБФ f₅(3), f₆(3) и f₇(3). Тип (0,2,0,0) имеют МБФ f₈(3), f₉(3) и f₁₀(3). Тип (0,0,2,0) имеют МБФ f₁₁(3), f₁₂(3) и f₁₃(3). Тип (0,1,1,0) имеют МБФ f₁₇(3), f₁₈(3) и f₁₉(3). Максимальными являются типы (1,0,0,0), (0,0,0,1), (0,3,0,0), (0,0,3,0), и (0,1,1,0).

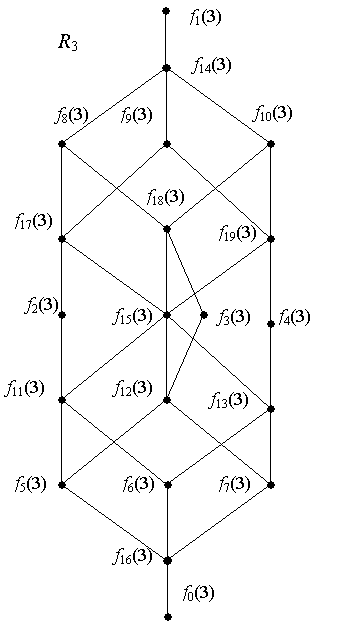Относительно операций дизъюнкции и конъюнкции все МБФ одного ранга образуют дистрибутивную решетку. Такие решетки R₀, R₁, R₂ и R₃ для рангов МБФ от 0 до 3 изображены на рис.1.

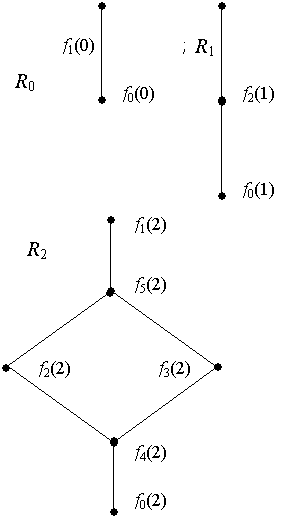
Рисунок 1 – Решетки МБФ R₀, R₁, R₂ и R₃.

Решетки R₁, R₂ и R₃ отличаются от свободных дистрибутивных решеток такого же ранга добавлением самой верхней и самой нижней вершин. Для типов и МБФ можно ввести матрицы распределения, в которых строка соответствует левой границе, а столбец правой границе. Обозначим через M_n и R_n матрицы распределения для максимальных типов и всех типов, а через G_n и F_n – матрицы распределения МБФ максимальных типов и всех МБФ ранга n. Для ранга 0 все четыре матрицы M₀, R₀, G₀ и F₀ одинаковы и имеют вид (1), т.е. состоят из одной строки и одного столбца. Для ранга 1 также все четыре матрицы M₁, R₁, G₁ и F₁ одинаковы и имеют вид . Для ранга 2 матрицы M₂ и G₂ имеют вид , R₂ = 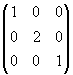и F₂ = 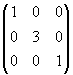. Для ранга 3 имеем M₃ = 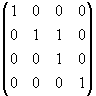, G₃ = 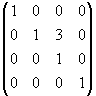, R₃ = 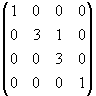и F₃ = . В матрицах R_n и F_n не учитывается тип из всех нулей и соответствующая ему МБФ f₀(n), т.к. в данном случае левая и правая границы не определены. В [3] показано, что типы ранга n+1 можно получать из типов ранга n с помощью операции сдвиг-суммы. В [4] доказана рекуррентное выражение, позволяющее по матрице M_n-1 находить матрицу M_n:

M_n = ^*M_n-1(^*T_n-2M_n-1)^* . (1)

Также доказано выражение:

R_n=⁺(R_n-1)+(R_n-1)⁺+⁺(R_n-1S_n-2⁺)(R_n-1)⁺. (2)

В (1) и (2) T_n-2 и S_n-2 это верхние треугольные матрицы размерности (n–1)(n–1),

причем у матрицы T_n-2 на главной диагонали расположены единицы, а у матрицы S_n-2 нули. Матрица ^*A получается из матрицы A добавлением сверху строки и слева столбца, состоящих из нулей, а на пересечении этих строки и столбца добавляется единица. Матрица A^* получается из матрицы A добавлением снизу строки и справа столбца, состоящих из нулей, а на пересечении этих строки и столбца добавляется единица. Матрица ⁺A получается из матрицы A добавлением сверху строки, а слева столбца, состоящих из нулей. Матрица A⁺ получается из матрицы A добавлением снизу строки, а справа столбца, состоящих из нулей. Таким образом M₃ = ^*M₂(^*T₁M₂)^*, а R₃=⁺(R₂)+(R₂)⁺+⁺(R₂S₁⁺)(R₂)⁺. Если допустить, что ^*T_-1= T_-1^*= =(1) и ⁺T_-1= T_-1⁺=(0), то все матрицы видов M_n и R_n рекуррентно порождаются выражениями (1) и (2) из матрицы (1) размерности 11.

f₁₇(3)

f₇(3)

В [5] на множестве МБФ любого ранга определены три унарные операции: двойственность, дизъюнктивное дополнение и конъюнктивное дополнение. Относительно этих операций МБФ ранга 3 распадаются на 4 блока по 5 элементов. На рис. 2 показан блок, порожденный МБФ f₂(3) = x₁.

f₁₁(3)

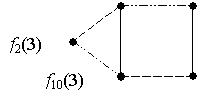
Рисунок 2 – Блок МБФ

На рис.2 указанные 3 операции изображены соответственно сплошной, штриховой и штрихпунктирной линиями. Для порождения из f₂(3) остальных МБФ достаточно применять по очереди вторую, а затем первую операции. Получаем цепочку МБФ: f₂(3), f₇(3), f₁₀(3), f₁₁(3), f₁₇(3). Аналогично можно получить цепочку f₃(3), f₆(3), f₉(3), f₁₂(3), f₁₈(3), цепочку f₄(3), f₅(3), f₈(3), f₁₃(3), f₁₉(3) и цепочку f₁₅(3), f₁₄(3), f₁₆(3), f₁(3), f₀(3)

Литература:

1. Ткаченко В.Г. Отказы цифровых схем и представления монотонных булевых функций / В.Г. Ткаченко //Наукові праці ОНАЗ ім. О.С. Попова. – Одеса, 2006. – №2. – С. 45 – 69.

2. Ткаченко В.Г. Классификация монотонных булевых функций при синтезе цифровых схем / В.Г. Ткаченко // Наукові праці ОНАЗ ім. О.С. Попова. – Одеса, 2008. – №1. – С. 35 – 43.

3. Ткаченко В.Г. Перечисления типов монотонных булевых функций при синтезе цифровых схем / В.Г. Ткаченко // Наукові праці ОНАЗ ім. О.С. Попова. – Одеса, 2008. – №2. – С. 54 – 69.

4. Ткаченко В.Г. Построение корректирующего кода для криптосистем на основе типов монотонных булевых функций / В.Г. Ткаченко, О.В. Синявский // Наукові праці ОНАЗ ім. О.С. Попова. – Одеса, 2010. – №1. – С. 85– 92.

5. Ткаченко В.Г. Взаимосвязь между матроидами и монотонными булевыми функциями электрических цепей/ А.М.Иваницкий, В.Г. Ткаченко //Наукові праці ОНАЗ ім. О.С. Попова. – Одеса, 2009. – №1. – С. 18 – 26.