Математика/5.Математическое моделирование

 

К. ф.‑м. н. Карнаух Т.А.

КНУ им. Т. Шевченко, Украина
Псевдометрика и ее свойства

 

При моделировании реальных объектов синтаксическими конструкциями зачастую оказывается, что некоторые объекты могут иметь несколько моделей. В этом случае семантическое расстояние между моделями уже не является метрикой, а потому теория пространств моделей не может рассматриваться как теория метрических пространств. Одним из возможных выходов является ослабление требований к метрике, который и рассматривается в данной работе.

Расстояния в пространствах. Согласно [1, с. 48], отображение d:X´X®[0;+¥), удовлетворяющее условиям:

"x, y ÎX d(x, y) = 0 Û x = y,

"x, yÎX d(x, y) = d(y, x)                      (аксиома симметрии),

"x, y, zÎX d(x, y) + d(y, z) £ d(x, z)      (неравенство треугольника),

называется метрикой, а сама пара (X, d) — метрическим пространством.

Рассмотрим некоторые логические свойства метрики.

Теорема 1. Построить метрику можно в пространстве любой мощности.

► В качестве доказательства введем на множестве X метрику d следующими правилами.

"xÎX d(x, x) = 0

"x, yÎX, x ¹ y d(x, y) = 1

◄

В [2, с. 378] в определении метрики опущена аксиома симметрии. На самом деле справедливо следующее утверждение.

Теорема 2. Все три аксиомы метрики независимы.

► Для множества X = {0, 1}w и расстояния d2(w, v) = |||w||2-||v||2| "w, uÎX (тут ||c1c2…||2 = 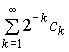) выполнены аксиомы симметрии и треугольника, но d2(0(1), 1(0)) = 0.

Для множества X = {a, b}, и расстояния d, заданного соотношениями :

d(a, a) = d(b, b) = 0, d(a, b) = 1, d(b, a) = 2,

первая аксиома метрики и аксиома треугольника выполнены, а аксиома симметрии — нет.

Для множества X = {a, b, c}, и расстояния d, заданного соотношениями :

d(a, a) = d(b, b) = d(c, c) = 0, d(a, b) = 1, d(b, a) = 1, d(a, с) = 1, d(с, a) = 1,

d(b, c) = 3, d(c, b) = 3,

выполнены все аксиомы метрики, кроме неравенства треугольника. ◄

Как обсуждалось в [3], в пространствах моделей бывает удобно иметь расстояние, согласно которому различные объекты могут оказываться на нулевом расстоянии. Понятно, что такое расстояние не является метрикой, поскольку не удовлетворяет первой аксиоме метрики. Рассмотрим, что произойдет, если первую аксиому метрики

"x, yÎX d(x, y) = 0 Û x = y

заменить на более слабую

"xÎX d(x, x) = 0.

Определение. Отображение d:X´X®[0;+¥), удовлетворяющее условиям:

"xÎX d(x, x) = 0                                  (аксиома равенства),

"x, yÎX d(x, y) = d(y, x)                      (аксиома симметрии),

"x, y, zÎX d(x, y) + d(y, z) £ d(x, z)      (неравенство треугольника),

будем называть псевдометрикой в пространстве X, а саму пару (X, d) — псевдометрическим пространством.

Теорема 3. В псевдометрическом пространстве (X, d) свойство точек быть на расстоянии 0 является эквивалентностью.

► Рефлексивность и симметричность очевидным образом выполняются. Проверим транзитивность.

d(x, y) = 0, d(y, z) = 0 Þ d(x, z) £ d(x, y) +d(y, z) £ 0 Þ d(x, z) = 0.

Поэтому отношение E: xE y Û d(x, y) = 0, является эквивалентностью. ◄

Количество n(x) = card{y | d(x, y) =0} точек пространства, на нулевом расстоянии от x, назовем кратностью точки x. Кратностью пространства назовем наибольшую из кратностей его точек (если таковая существует).

Для метрики из первой аксиомы метрики следует, что "xÎX  n(x) = 1. Таким образом, метрическое пространство имеет кратность 1. Кратность псевдометрического пространства, не являющегося метрическим, не может быть менее 2. К примеру, кратность псевдометрического пространства ({0, 1}w, d2) в точности равна 2. Имеет смысл отдельно рассматривать пространства конечной кратности. В частности, добавлением к аксиомам псевдометрики аксиомы кратности

"xÎX  n(x) £ k

можно ввести понятие k‑кратного псевдометрического пространства.

Теорема 4. Точки на расстоянии 0 имеют одинаковые кратности, то есть

 d(x, y) = 0 Þ n(x) = n(y).

► Утверждение следует из того, что n(x) = card[x]E, где xEy Û d(x, y) = 0. ◄

Теорема 5. Если d(x1, x2) = 0, то d(x1, y) = d(x2, y).

► Из аксиом псевдометрики следует, что

d(x1, y) £ d(x1, x2)+ d(x2, y) = 0 + d(x2, y) = d(x2, y).

Неравенство  d(x2, y) £ d(x1, y) доказывается аналогично. ◄

Доказанное утверждение дает право рассматривать фактор-пространство X/E с расстоянием dE([x]E, [y]E) = d(x, y).

Теорема 6. Пространство (X/E, dE) является метрическим.

Заметим, что для псевдометрического пространства моделей (M, dS) [3], построенного по пространству реальных объектов (X, dX), в метрике пространства (M/E, dE) расстояние между классами моделей совпадает с расстоянием между соответствующими реальными объектами в пространстве (X, dX).

Интересно рассмотреть, что изменится с точки зрения математического анализа при переходе от метрического пространства к псевдометрическому, а также, что останется в силе.

Предел последовательности точек. Как и в случае классического метрического пространства, будем говорить, что последовательность (xn)nÎN точек пространства X сходится к точке xÎX, если  d(xn, x) = 0.

Утверждение 7. Если последовательность (xn)nÎN точек пространства X имеет несколько различных пределов, то все попарные расстояния между ними равны 0.

► Пусть  d(xn, x) =  d(xn, y) =0. Тогда

0 £ d(x, y) £ d(x, xn) + d(xn, y).

Переходя в полученных неравенствах к пределу при n®0, получаем d(x, y) = 0, что и требовалось показать. ◄

Непрерывность функции. Пусть даны два метрические пространства реальных объектов (X, dX) и (Y, dY), а также два псевдометрические пространства (MX, dX) и (MY, dY), в которых псевдометрика соответствует семантической эквивалентности их моделей (а потому и обозначена как метрика соответствующего пространства). Пусть dX1 и dY1 задают согласованные [3] синтаксические расстояния в пространствах MX и MY, то есть синтаксически близкие элементы являются близкими и семантически.

В классическом случае понятие непрерывного отображения метрического пространства рассматривается относительно метрики [1, с.51]. Несколько обобщим определение. Будем говорить, что функция f (d1, d2)‑непрерывна в точке x0 пространства Z, если

"e>0 $d>0 "xÎZ (d1(x0, x)<d ® d2(f(x0), f(x))< e).

Таким образом, (dX1, dY1)‑непрерывность соответствует классической непрерывности в метрических пространствах. С точки зрения алгоритмических устройств это абсолютно естественное понятие: синтаксически близкие входы должны преобразовываться в синтаксически близкие объекты. Тут следует заметить, что перенос непрерывного отображения fM:MX ® MY в пространство реальных объектов f: X®Y по правилу f(x) = fM(n¢(x)), где отображение n¢ по элементу восстанавливает некоторую его модель, может приводить к тому, что отображение f утратит непрерывность (в смысле метрик dX и dY) в точках, имеющих несколько моделей.

Если рассматривать теорию R‑преобразователей [4], то заданная R‑преобразователем словарная функция является (dX1, dY1)‑непрерывной (синтаксически близкие входы перерабатываются в синтаксически близкие выходы). Кроме того, введенное в работе [4] понятие частично непрерывной функции соответствует (dX1, dY)‑непрерывности. В силу того, что синтаксическое и семантическое расстояния dY1 и dY  согласованы, (dX1, dY1)‑непрерывное отображение является и  (dX1, dY)‑непрерывным. Для непрерывности отображения f: X®Y необходимо требовать (dX, dY)‑непрерывность для fM.

(dX, dY)‑непрерывное в точке отображение fM:MX ® MY  псевдометрических пространств будем называть псевдонепрерывным в точке.

Свойства псевдонепрерывных отображений. Для упрощения изложения далее рассматриваем псевдонепрерывное отображение f из псевдометрического пространства (X, dX) в псевдометрическое пространство (Y, dY). Будем говорить, что фукнция f имеет псевдопредел a в точке x0, если

"e>0 $d>0 "xÎZ (dX(x0, x)<d ® dY(a, f(x))< e),

и обозначать это так a Î f(x).

Теорема 8. a, bÎf(x) Þ dY(a, b) = 0.

► Справедливость утверждения следует из того, что

0 £ dY(a, b) £ dY(a, f(x)) + dY(f(x), b) = dY(a, f(x)) + dY(b, f(x)) ® 0 при x®x0. ◄

Теорема 9. aÎf(x) , dY(a, b) = 0 Þ bÎf(x) .

►0 £ dY(b, f(x)) £ dY(b, a) + dY(a, f(x)) = dY(a, f(x)) ® 0 при x®x0. ◄

Таким образом, если псевдонепрерывная функция имеет несколько псевдопределов в точке, то все они эквивалентны (расстояние между ними равно 0). И каждое из эквивалентных значений является псевдопределом, если таковым является хотя бы одно.

Кроме того, следует отметить, что, аналогично классическому математическому анализу, определения псевдонепрерывности и псевдопредела по Гейне эквивалентны приведенным тут определениям по Коши.

При работе с моделями чаще всего мы имеем дело с псевдометриками. Дальнейшим продолжением данного исследования будет описание и построение псевдометрических пространств моделей для реальных пространств, с псевдометриками, которые согласованы с метрикой реального пространства. Данный метод позволит предложить качественно новый подход к решению задач распознавания и классификации в целом.

 

Литература:

1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1976. – 544 с.

2. Корн Г., Корн Т. Справочник по математике. – М.:Наука, 1973. – 832 с.

3. Карнаух Т.А. Метрики в пространствах моделей. // Материалы II Международной научно-практической конференции "Новости научной мысли – 2010".

4. Лисовик Л. П. Логические свойства частично непрерывных функций. // Тр. ин-та математики СО АН СССР. – Математическая логика и алгоритмические проблемы. Н.: Наука, 1989. – Т. 12. – С. 39-72.

 

e-mail: tkarnaukh@unicyb.kiev.ua