Ибрагимов У.М., Бахбердиева К.М.
Южно-Казахстанский
государственный университет им. М.Ауезова,
г.Шымкент, us-ibr@rambler.ru
![]() О задаче оптимального перехода
О задаче оптимального перехода
под воздействием управления
1. Постановка задачи. Пусть управляемый
объект описывается уравнением
![]() (1)
(1)
где ![]()
![]() мерный вектор евклидова пространства
мерный вектор евклидова пространства ![]()
![]() постоянная матрица порядка
постоянная матрица порядка ![]()
![]() управляющий параметр,
управляющий параметр, ![]() непустое подмножество пространства
непустое подмножество пространства ![]() . В пространстве
. В пространстве ![]() выделено непустое подмножество
выделено непустое подмножество ![]() , которое называется
терминальным.
, которое называется
терминальным.
Определение 1. Будем говорить, что из
точки ![]() возможен переход
на
возможен переход
на ![]() , если существует измеримая
функция
, если существует измеримая
функция ![]() ,
, ![]() , такая, что решение
, такая, что решение ![]() ,
, ![]() уравнения
уравнения
![]() ,
,
![]() (2)
(2)
при ![]() попадает на
попадает на ![]() , т.е.
, т.е. ![]() . Время
. Время ![]() будем называть
временем перехода из точки
будем называть
временем перехода из точки ![]() на множество
на множество ![]() .
.
Определение 2. Время перехода ![]() из точки
из точки ![]() на множество
на множество ![]() называется
оптимальным, если для произвольного времени перехода
называется
оптимальным, если для произвольного времени перехода ![]() имеет место
неравенство
имеет место
неравенство ![]()
2. Основная часть. Через ![]() обозначим
пространство всех подмножеств
обозначим
пространство всех подмножеств ![]() , через
, через ![]() - пространство всех замкнутых, через
- пространство всех замкнутых, через ![]() пространство всех компактных подмножеств пространства
пространство всех компактных подмножеств пространства ![]() .
.
Пусть ![]() ,
, ![]() произвольная функция со значениями в пространстве
произвольная функция со значениями в пространстве ![]() Интегралом
Интегралом 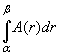 называется множество тех и только тех точек
называется множество тех и только тех точек ![]() , для каждой из которых существует суммируемая функция
, для каждой из которых существует суммируемая функция ![]() ,
, ![]() , такая, что
, такая, что 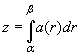 ,
, ![]() для почти всех
для почти всех ![]() . В дальнейшем, изменив, если нужно, значения функции
. В дальнейшем, изменив, если нужно, значения функции ![]() ,
, ![]() на множестве меры
нуль, будем считать, что
на множестве меры
нуль, будем считать, что ![]() при всех
при всех ![]() .
.
Через ![]() ,
, ![]() , обозначим множество
, обозначим множество 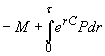 ; при
; при ![]() положим
положим ![]() . Имеет место следующая.
. Имеет место следующая.
Лемма. Для возможности перехода из точки ![]() на
на ![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
![]() (3)
(3)
для некоторого ![]() .
.
Доказательство. Достаточность условия (3). Имеем ![]() . По определению алгебраической суммы множеств в векторном
пространстве
. По определению алгебраической суммы множеств в векторном
пространстве ![]() существует точки
существует точки ![]() и
и ![]() , такие, что
, такие, что ![]() . По определению же интеграла от функции
. По определению же интеграла от функции ![]() ,
, ![]() , существует симмируемая функция
, существует симмируемая функция ![]() ,
, ![]() , для которой
, для которой 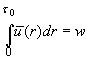 ,
, ![]() для всех
для всех ![]() . Ввиду гомеоморфности отображения
. Ввиду гомеоморфности отображения ![]() суммируемой будет и
функция
суммируемой будет и
функция ![]() ,
, ![]() . Очевидно, что
. Очевидно, что ![]() для всех
для всех ![]() . Такими же свойствами обладает и функция
. Такими же свойствами обладает и функция ![]() ,
, ![]() .
.
Покажем, что под воздействием управления ![]() ,
, ![]() фазовая точка
переходит из
фазовая точка
переходит из ![]() на
на ![]() . Действительно, для решения
. Действительно, для решения ![]() ,
, ![]() , уравнения (2) соответствующего управлению
, уравнения (2) соответствующего управлению ![]() ,
, ![]() , имеем
, имеем
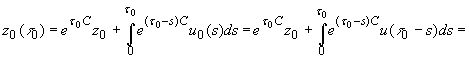
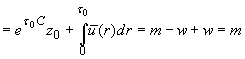 . (4)
. (4)
Необходимость условия (3). Ввиду
автономности уравнения (1) все управления можно считать определенными на
сегментах вида ![]() .
.
Ясно, что если под воздействием управления ![]() ,
, ![]() фазовая точка
переходит из
фазовая точка
переходит из ![]() на
на ![]() , то для решения
, то для решения ![]() ,
, ![]() имеем
имеем
![]()
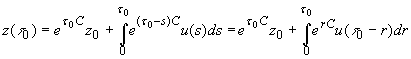 (5)
(5)
Очевидно, функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() , суммируемы и
, суммируемы и ![]() ,
, ![]() , для почти всех
, для почти всех ![]() . Поэтому
. Поэтому
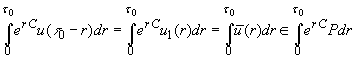 .
.
Так как ![]() , то
, то 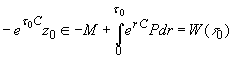 .
.
Лемма доказана полностью. С помощью леммы можно получить
полное описание тех точек, из которых возможен переход на ![]() .
.
3. Вывод. Для возможности перехода
из точки ![]() на
на ![]() необходимо и
достаточно, чтобы
необходимо и
достаточно, чтобы 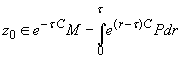 для некоторого
для некоторого ![]() .
.
Л и т е р а т у р а
1. Понтрягин
П.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория
оптимальных процессов. М., "Наука", 1969
2. Ibragimov
U.M. Task of vitality in discrete inclusions. Nauka i
studio. NR 6 (11), 2008. Techniczne nauki. p.74-77.