М. Б. Вакарчук

Днепропетровский национальный университет имени О. Гончара

НЕРАВЕНСТВА ТИПА КОЛМОГОРОВА ДЛЯ НАИЛУЧШИХ ПРИБЛИЖЕНИЙ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ИЗ ПРОСТРАНСТВА ХАРДИ

С начала прошлого века особый интерес у многих математиков, начиная с Э. Ландау, Ж. Адамара, Г. Харди, Дж. Литтльвуда, А. Н. Колмогорова, вызывает получение точных неравенств для норм промежуточных производных функции через норму самой функции и норму ее старшей производной. Современное развитие этой тематики связано с работами В. В. Арестова, С. Б. Стечкина, Л. В. Тайкова, В. Н. Габушина, Н. П. Купцова, А. Ю. Шадрина, В. М. Тихомирова, Н. П. Корнейчука, В. Н. Коновалова, В. Ф. Бабенко, А. А. Лигуна, С. А. Пичугова, В. А. Кофанова, Г. Г. Магарил-Ильяева и многих других [1].

Не меньший интерес представляет решение подобных задач и в случае аналитических функций комплексного переменного, где по сравнению с вещественным случаем не так много окончательных результатов Введем необходимые обозначения и понятия.

Пусть , A(U) – множество функций, аналитических в круге U; – банахово пространство Харди, состоящее из функций , для которых конечна норма

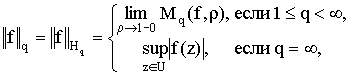
где .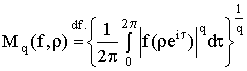

Известно, что норма функции реализуется на ее угловых граничных значениях , которые существуют почти для всех [2].

Пусть – точка двумерного комплексного пространства ; – единичный бикруг в ; – остов бикруга.

Класс всех аналитических в функций обозначим через . Пусть и

.

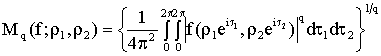Символом () обозначим пространство Харди в , состоящее из функций , для которых конечна норма

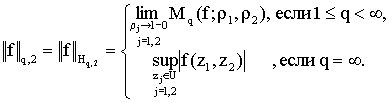
Из результатов А. Зигмунда [3] следует, что для функции почти всюду на существуют угловые граничные значения, выполняется равенство

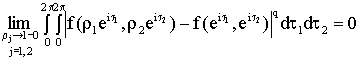
и функцию f можно считать заданной почти всюду на . Поэтому под часто подразумевают именно множество таких граничных функций и говорят, что норма реализуется на ее угловых граничных значениях , которые существуют почти для всех .

Символом обозначим множество функций , у которых смешанные производные по переменным и и частные производные по переменной и по переменной принадлежат пространству .

Пусть – алгебраический многочлен степени по переменной , а – алгебраический многочлен степени по переменной .

Величину

–

назовем наилучшим приближением функции двумерным «углом» по переменным . Имеет место следующая

Теорема. Пусть – натуральные числа, . Тогда для любой функции справедливы неравенства

,

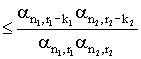
Литература:

1. Бабенко, В. Ф. Неравенства для производных и их приложения / В. Ф. Бабенко, Н. П. Корнейчук, В. А. Кофанов, С. А. Пичугов. – К., 2003. – 590 с.

2. Гофман, К. Банаховы пространства аналитических функций / К. Гофман. – М., 1963. – 312 с

3. Zigmund A. On the boundary values of functions of several complex variables / A. Zigmund // Fund. Math. – 1949. – V. 36 – P. 47 – 59