Физика / 2.Физика твердого тела

Губарев А.А., к. ф.-м. н. Яковлев Д.А.

Донецкий национальный университет

Моделирование методом Монте-Карло начальных этапов формирования рельефа поверхности аморфной мишени, учитывающее диффузионную релаксацию плотности

В данной работе продолжено (начатое в [1, 2, 3]) исследование методом Монте-Карло формирования рельефа на изначально плоской поверхности аморфного твердого тела при облучении пучком ионов. В [1] детально описана схема моделирования, не учитывающая изменение мишени в объеме. При моделировании, описанном в [2, 3], на поверхность мгновенно переносились вакансии и междоузельные атомы образованные только в поверхностном и приповерхностном слое; вакансии и междоузельные, образовавшиеся на больших глубинах, участвовали в формировании поверхности только после того, как в результате распыления, ячейки с этими вакансиями и междоузельными становились поверхностными. Вакансия, образующаяся на большем удалении от поверхности, может лишь рекомбинировать с существующим в некоторой её окрестности (рекомбинационный объем) междоузельным, аналогично, образующийся междоузельный может рекомбинировать с существующей в некоторой его окрестности вакансией. Поскольку вакансии, в среднем, образуются ближе к поверхности, чем междоузельные, в глубине могут формироваться области, которые будут содержать слишком много избыточных атомов. Для предотвращения этого по достижению некоторого порогового максимального значения избыточных атомов в окрестности точки остановки, избыточный атом переносится за её границу (объемная релаксация по достижению порогового значения). При моделировании по этой схеме на поверхности формируется рельеф с большей длиной волны по сравнению с рельефом, рассчитанным по предыдущей схеме; на тыльных сторонах склонов не формируется, не наблюдаемых в эксперименте и не учитываемых в модели, вертикальных участков.

В модели данной работы каскад столкновений рассчитывается, как и в [1–3], а релаксация выполнялась, как за счет попадании дефекта в рекомбинационный объем дефекта другого типа, так и за счет за счет диффузии междоузельных атомов с учетом энергии взаимодействия междоузельных атомов между собой и с вакансиями. Рекомбинационный объем был выбран, как и в [2, 3], равным 27-ми вычислительным ячейкам. В результате диффузионного скачка атом может перейти из позиции в одно из шести ближайших положений с частотой

,

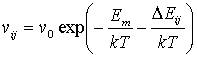где — частота собственных колебаний (полагаемая равной  Гц), — энергия миграции междоузельного атома (полагаемая равной 1 эВ), приращении энергии взаимодействия междоузельного атома с окружающими вакансиями и междоузельными атомами при переходе атома из положения в положение . Для энергии взаимодействия двух дефектов использовано простейшее выражение , где — длина ребра вычислительной ячейки; — расстояние между дефектами; — коэффициент, абсолютное значение которого полагалось равным эВ; имел знак плюс, при взаимодействии двух междоузельных атомов, и знак минус, при взаимодействии междоузельного атома и вакансии. При расчете энергии взаимодействия учитывались взаимодействия с атомами в окрестности 7×7×7 ячеек. Моделирование выполнялось по следующей схеме. В соответствии с частотой диффузионных скачков атомов и частотой падения ионов на моделируемый участок поверхности, на очередном шаге расчета выполняется: либо расчет каскада в приближении бинарных столкновений, либо выполняется диффузионное перемещение одного из междоузельных атомов. После расчета каждого каскада столкновений и после каждого диффузионного скачка, пересчитываются частоты диффузионных скачков атомов, в окружении которых произошли изменения.

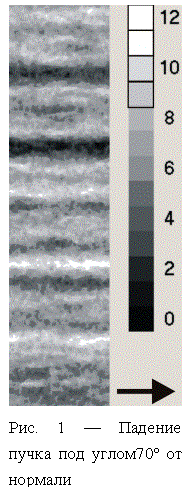
Было выполнено моделирование облучения ионами Ar с энергией 1 кэВ мишени Si под углами 30° и 70° от нормали к исходной плоской поверхности образца. На рис. 1 и 2 высоты поверхности отображены оттенком серого: чем участок выше, тем он светлее; стрелкой помечено направление падения пучка; высоты на цветовой шкале отложены в единицах длин вычислительной ячейки, Å. На рис. 1 отображен рельеф, сформировавшийся при облучении под углом 70° и дозе 8.3×10¹⁶ см^–2 (65 иона на атом). От начала облучения и до дозы приблизительно 1.0·10¹⁶ см^–2 (8 ионов на атом) число междоузельных атомов возрастает, а, начиная с указанной дозы, испытывает очень слабые колебания вокруг среднего значения, которое не меняется с увеличением дозы моделирования (см. линию 1 на рис. 3). Среднеквадратичное отклонение высот растет при всех значениях дозы достигая, при наибольшей рассчитанной дозе (8.3×10¹⁶ см^–2), значения 2.9.

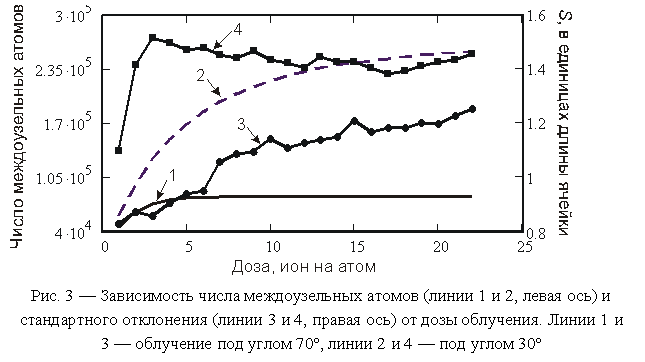
Моделирование облучения под углом 30º выполнялось до дозы 2.8·10¹⁶ см^–2 (22 иона на атом), насыщения числа междоузельных атомов не наблюдалось (см. лин. 2 на рис. 3). На начальном этапе облучения (до 5 ион на атом поверхности, т.е. до 0.6·10¹⁶ см^–2) растет размах и среднеквадратичное отклонение высот поверхности). Начиная с дозы 0.6·10¹⁶ см^–2, рост размаха прекращается, среднеквадратичное отклонение убывает.

В процессе моделирования не возникали области объема 3×3×3 атома, в которых все ячейки содержали бы избыточные атомы. Т.е. диффузионного механизма было достаточно для релаксации плотности.

Литература:

1. Губарев А.А., Яковлев Д.А. Вісник Донецького національного університету, Сер. А: Природничі науки. – 2009. – вип. 2. – C. 198–205.

2. Губарев А.А. Известия РАН. Серия физ. – 2008. – том 72. – N. 5. – С. 632–635.

3. Губарев А.А. Известия РАН. Серия физ. – 2010. – том 74. – № 2 – С. 153–158.