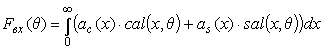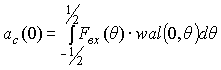Технические науки / 12. Автоматизированные системы управления на производстве

Kulyk A.J., Kulyk J.A, Kulyk A.A.

Vinnytsia national technical university, Ukraine

Аналіз впливу амплітудних спотворень сигналів The analysis of amplitude distortion of signals

каналом зв'язку в базисі функцій Уолша communication channel in basis Walsh functions

The literature shows that the analysis of influence communication channel for the transfer process can be carried out not only the sine and cosine, but also other types of orthogonal functions [1]. Using the sine basis functions due to the simplicity of transient analysis for circuits with passive elements, is invariant to time, which is the coil inductance, capacitors and resistors. In this case the equipment can be described by differential equations with constant coefficients. Sine voltage is applied to the entrance of such a scheme, as shown on the output voltage amplitude with a lower phase shift, but the S-shape and frequency are stored. In practice, the transfer of information technology, mainly used rectangular signals. It is reasonable and cross-impact communications and signals when transmitting information to bases in rectangular orthogonal Walsh or the Haar functions [2]. A similar analysis for synusopodibnyh functions is quite common [3, 4], although not always convenient.

Any complete system of orthogonal functions f(j, θ) can be divided into even functions f _s (j, θ), odd f_s (j, θ) and the permanent component of f(0, θ). For Walsh functions basis functions are paired cal ( j , θ ), odd – sal ( j , θ ), and the constant component – wal (0, θ ). In this case the input entrance of F_вх(θ) may be filed as

. (1)

Ratios a _c and a _s are based on equations

, ;

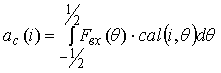, ; (2)

, .

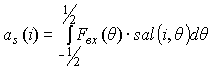Given the specific features of Walsh functions to replace the integral representation of bounded time function signal entrance of F _вх ( θ ) a sum of components [2]

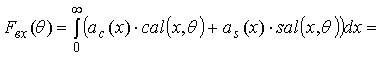
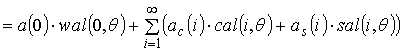. (3)

Given that

, (4)

where K ( θ ) – coefficient of transmission channel.

In the simplest case channel carries only the amplitude distortion (attenuation or gain). This factor K ( θ ) can be represented as a number of composition is also determined basis Walsh functions

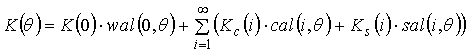. (5)

Let this number is limited to a constant component and the first even harmonic

. (6)

Then the output channel signal will be

(7)

Given the rules of transformation products of odd and even Walsh functions described in the literature [2], expression (7) can be represented as

(8)

If the number that describes the rate of conversion of feed to restrict only to the first component and odd harmonics

, (9)

then the signal on the output channel will look like

(10)

If the specified limited number of fixed component and the first odd and even harmonic

, (11)

channel output signal takes the form

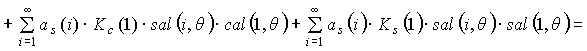
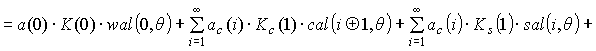
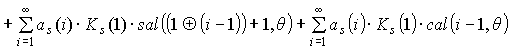. (12)

If the number is limited only even harmonic

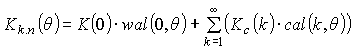, (13)

the reference signal channel expression can be described

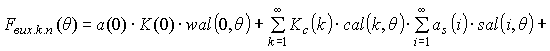
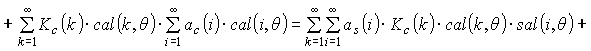
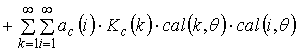. (14)

Similarly you can define output for the case when the number is limited only odd harmonics

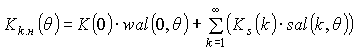, (15)

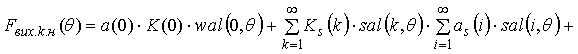
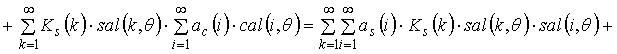
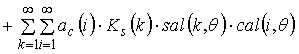. (16)

The expressions show that in all cases, changing only the frequency components of the signal spectrum, unlike the case when the test is done in Fourier basis functions. The latter is formed without the final number of components that precede and late in relation to the informative signal [5]. Thus, the analysis functions in the basis Walsh functions greatly simplifies the process of transfer and construction of hardware and software in this basis to release the channel from echo signals which significantly complicate the process of transmitting information.

REFERENCES:

1. Хармут Х.Ф. Теория секвентного анализа. Основы и применения. – М.: Мир, 1980. – 574 с.

2. Хармут Х.Ф. Передача информации ортогональными функциями. – М.: Связь, 1975. – 272 с.

3. Квєтний Р.Н., Компанець М.М., Кривогубченко С.Г., Кулик А.Я. Основи техніки передавання інформації. – Вінниця: УНІВЕРСУМ-Вінниця, 2002 – 358 с.

4. Кулик А.Я., Компанец Н.Н., Кривогубченко Д.С. Энергетический спектр сигналов при передаче информации оптическими линиями связи // Вимірювальна та обчислювальна техніка в технологічних процесах. – 2000. – № 1. – С. 50 – 51.

5. Кулик. А.Я. Аналіз впливу каналу зв’язку на процес передавання інформації. // Оптико-електронні інформаційно-енергетичні технології, 2002. – № 1. – С. 170 – 173.