Мельник В.Н., Карачун В.В.

Национальный технический университет Украины «КПИ»

ПОРИСТАЯ ПЛАСТИНА В АКУСТИЧЕСКОМ ПОЛЕ

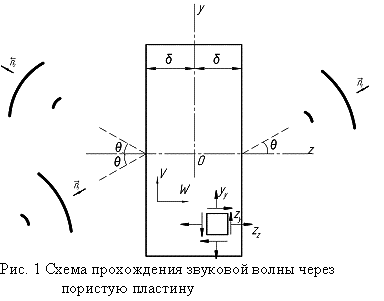Расчетная модель прохождения звука представлена на рис. 1. Здесь оси параллельны плоскости падающей волны. Математическая модель взаимодействия системы «пластина-воздух в порах» при падении звуковой волны со стороны открытых пор может быть представлена в виде. Уравнение, которое описывает движение скелета пластины, и уравнения, описывающего движение воздуха в порах жесткого скелета –

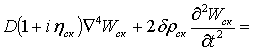
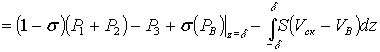; (1)

, (2)

где индекс «ск» ставится у величин, относящихся к скелету, индекс «в» – относящихся к воздуху; смещение скелета; колебательная скорость скелета; колебательная скорость воздуха в порах в направлении оси ; звуковое давление в воздухе, заключенном в порах; плотность материала скелета (масса скелета на единицу объема пластины); плотность воздуха в пластине (масса воздуха в порах в единице объема пластины); , плотность свободного воздуха; цилиндрическая жесткость пластины на изгиб; коэффициент потерь скелета; модуль упругости воздуха; сила взаимодействия между скелетом и воздухом в порах, отнесенная к единице объема пластины, при разности равной единице; давления в падающей, отраженной и прошедшей волнах соответственно; .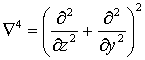

Правая часть уравнения (1) представляет собой силовые факторы, действующие на пластину. Так, первое слагаемое отображает звуковое давление на лицевой поверхности пластины, второе слагаемое звуковое давление на теневой стороне пластины (давление в прошедшей волне), третье слагаемое давление воздуха в порах на закрытые части пор, расположенные на теневой стороне пластины, четвертое слагаемое 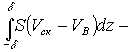определяет давление воздуха в порах на скелет

Рассмотрим пористую пластину, конструктивно выполненную таким образом, что поры закрыты с обеих сторон, и проанализируем изменение ее динамических свойств под действием падающей звуковой волны.

В отличие от известного, в этом случае видоизменится правая часть уравнения движения –

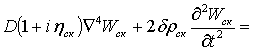
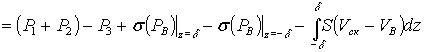, (3)

а уравнение движения воздуха в порах и уравнение непрерывности

, (4)

останутся без изменений. Граничные условия для скелета пластины примут вид

; , (5)

а для воздуха в порах –

. (6)

Решив систему уравнений с учетом граничных условий (5), (6), получим закон изгибных колебаний пористой пластины при акустическом нагружении.

Анализ показывает, что повышение звукоизоляционных свойств таких конструкций, по сравнению со сплошными, незначительно и им можно пренебречь. Однако на резонансных частотах возможно резкое снижение звукоизоляции, что необходимо учитывать.

Количественный анализ генерируемой в пористой пластине вибрации удобно, как и в предыдущих случаях, проводить по ее пространственным характеристиках, т.е. длине и амплитуде изгибной волны. Так как при этом полагаем время , то выражение (3) существенно упрощается –

.

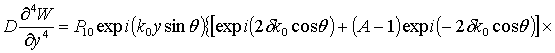
Техническая реализация конструкции, которая может быть приведена к предлагаемой расчетной модели, может быть не только в виде пластины, но и в виде их сочетания, в том числе, композиционного состава.