Технические науки/2. Механика
Рыстыгулова
В.Б.
Казахский
Национальный Педагогический Университет имени Абая,
Республика
Казахстан
ОСЕСИММЕТРИЧНЫЙ ИЗГИБ СФЕРИЧЕСКОЙ
ОБОЛОЧКИ
В работах [1-3] рассмотрены задачи о осесимметричной
деформации конической оболочки при постоянных и переменных нагрузках, приведены
общее решение задачи осесимметричной деформации конической оболочки для любого
закона изменения внешних нагрузок. Также решена задача осесимметрично
нагруженной оболочки вращения [4].
Теория тонких оболочек является одним из
актуальных разделов теории упругости и широко используются в машиностроении,
авиастроении, судостроении.
Рассмотрим
сферическую оболочку для ![]() .
.
Разрешающие
дифференциальные уравнения получены Майснером /5/:
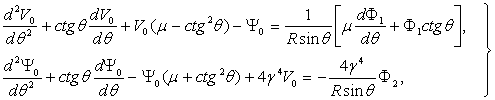 (1)
(1)
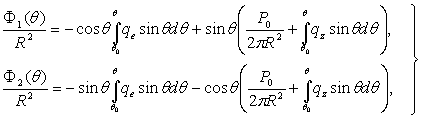 (2)
(2)
где ![]() силовая функция,
силовая функция, ![]() функция перемещений,
функция перемещений, ![]() составляющие распределенной внешней нагрузки в радиальном
и осевом направлениях,
составляющие распределенной внешней нагрузки в радиальном
и осевом направлениях, ![]() постоянная интегрирования, равная осевому усилию в
крайнем сечении
постоянная интегрирования, равная осевому усилию в
крайнем сечении ![]() (
(![]() ).
). ![]() - параметр,
характеризующий относительную толщину оболочки.
- параметр,
характеризующий относительную толщину оболочки.
Рис.1. Сферическая оболочка
Дискретизация третих, четвертых
членов системы уравнения (1), дает:
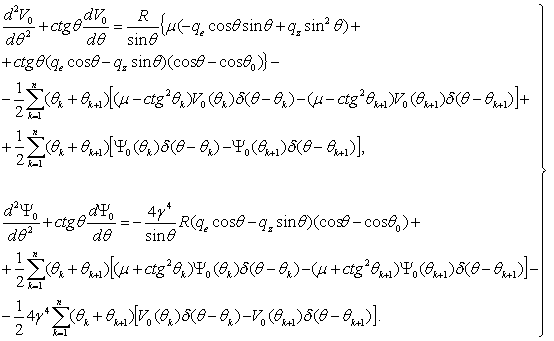 (3)
(3)
Методом
частичной дискретизаций нелинейных дифференциальных уравнений получим следующее
решение системы (3):
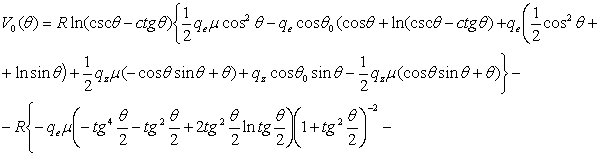 (4)
(4)
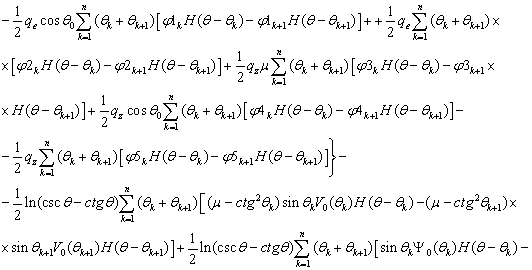
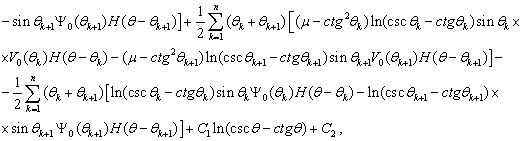
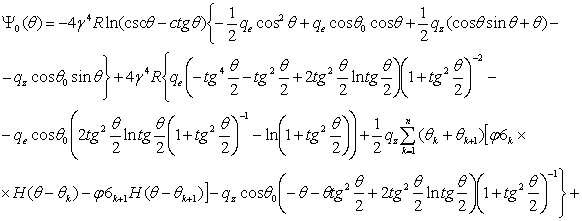 (5)
(5)
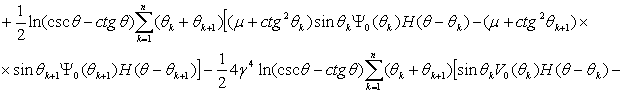
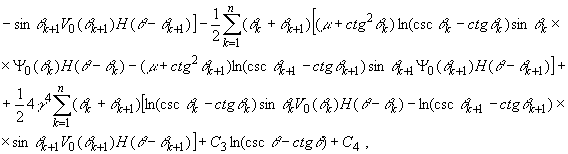
где
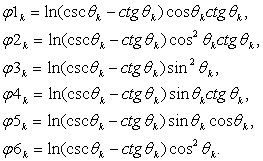 (6)
(6)
Примем следующие граничные условия
1)
![]() при
при ![]() (7)
(7)
2)
![]() при
при ![]()
где
![]() радиальное усилие,
радиальное усилие, ![]() меридиональный
изгибающий момент,
меридиональный
изгибающий момент, ![]() радиальное
перемещение,
радиальное
перемещение, ![]() угол поворота,
и
угол поворота,
и
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Постоянные интегрирования ![]() ,
, ![]() ,
, ![]() ,
, ![]() находятся из
граничных условий (7).
находятся из
граничных условий (7).
Построены поля меридиональных и окружных
растягивающих усилий и изгибающих моментов.
Построены
графики зависимости угла поворота сферической оболочки для ![]() (
(![]() ),
), ![]()
![]()
![]() ,
, ![]() см,
см, ![]() см. Для расчета
использована программа MathCad.
см. Для расчета
использована программа MathCad.
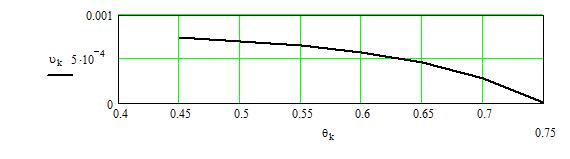
График конкретных значений нагрузок
иллюстрирует закономерность изгиба оболочки под воздействием и указанных выше
способов закрепления границ.
В отличии от результатов В.С. Черниной [6]
полученных для однородной системы уравнений в настоящей работе получены
аналитические решения для задачи (1), (7) с учетом правой части
дифференциальных уравнений (1).
Работа выполнена в рамках научной программы по фундаментальным
исследованиям МОН РК «Решений актуальных прикладных задач механики твердого и
деформируемого твердого тела методами Каппа-функции, частичной дискретизации
нелинейных дифференциальных уравнений» (№ госрегистрации: 0106РК00638).
Литература
1.
Тюреходжаев А.Н., Рыстыгулова В.Б.
Осесимметричная деформация конической оболочки // Материалы Международной
научно-технической конференции «Наука, образование, инновации: приоритетные
направления развития», посвященной 55-летнему юбилею Кыргызского
государственного технического университета им. И. Раззакова, 16-18 сентября
2009 г., Бишкек. 5 стр.
2.
Тюреходжаев А.Н., Рыстыгулова В.Б.
Аналитическое решение задачи о осесимметричном изгибе тонкостенной конической
оболочки // Труды Международной научно-практической конференции «Механика и
строительство транспортных сооружений», посвященная 75-летию Заслуженного
деятеля науки РК, академика НАН РК, д.т.н., профессора Айталиева Ш.М., 28-29
января 2010 г., Алматы. С.117-123
3.
Тюреходжаев А.Н., Рыстыгулова В.Б. Аналитическое решение уравнений Мейснера методом
частичной дискретизации // Международная научно-техническая
конференция «Современные проблемы геотехники, механики и
строительства транспортных сооружений», посвященная 70-летию д.т.н.,
профессора, академика МАИН Исаханова Е.А., 28-29 мая 2010 г., Алматы. 3 стр.
4.
Тюреходжаев А.Н., Рыстыгулова В.Б. Аналитическое решение задачи осесиметрично нагруженной
оболочки вращения // Международная научно-техническая
конференция «Третьи Ержановские чтения», посвященная 20-летию НИА
РК, 21-22 мая 2010 г., Актюбе. С.291-295
5.
Мeissner E.,
Über Elastizität und Festigkeit dünner Schalen,
Vierteljahrschrift der Naturforschenden Gesellschaft in Zürich, Jahrgang
60, 1915.
6.
Чернина В.С. Статика
тонкостенных оболочек вращения. Главная редакция физико-математической
литературы издательства «Наука», 1968, 456 с.