Бурцев Игорь Олегович

Иркутский национальный исследовательский технический университет, Россия

Позиционный принцип минимума в дискретных задачах оптимального управления. Анализ негативного примера

Дискретные процессы управления приобретают все большее значение в теории и практике оптимального управления. Это связано с тем, что многие задачи экономического планирования, технологии и организации производства, исследования операций, военного дела описываются разностными уравнениями, так как на практике чаще всего и информация о состоянии процесса, и управление процессом осуществляются в дискретные моменты времени, т.е. по шагам.

Для решения таких многошаговых задач возможны два подхода. Один из них – вариационный – подход основан на распространении идей и методов математического программирования на многошаговые задачи и смыкается с аппаратом принципа максимума Л.С.Понтрягина, развитого для решения задач оптимального непрерывного управления. Этот подход иногда называют «дискретный принцип максимума» (ДПМ).

Поскольку задачи дискретного оптимального управления фактически являются задачами математического программирования специальной структуры, то для них в общем случае не имеет места аналог принципа максимума Понтрягина – фундаментальное необходимое условие оптимальности в непрерывных задачах оптимального управления. Тем не менее, значительные усилия математиков были посвящены выделению классов задач дискретного оптимального управления, в которых принцип максимума справедлив, возможно в несколько ослабленной форме «квазимаксимума» [1; 2; 3].

В данной работе проводится аналитическое исследование негативного примера дискретной задачи из [3, с. 256]. Будем исследовать пример, исходя из следующей схемы:

а) функционал представляется как явная функция от управления;

б) проводится решение задачи при помощи ДПМ. Составляется функция Понтрягина и сопряженная система . Находится решение сопряженной системы и решается задача ;

в) вводится расширенная функция Понтрягина . Сопряженная система решается при заданном оптимальном управлении. Решаются задачи минимизации .

г) применяется позиционный принцип минимума в качестве схемы улучшения неоптимального управления.

В следующем примере не только не выполняется дискретный принцип максимума, но функция Понтрягина достигает своего минимума вдоль любого допустимого управления.

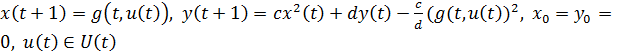
– произвольно, 

 – произвольны,

Вычислим явно

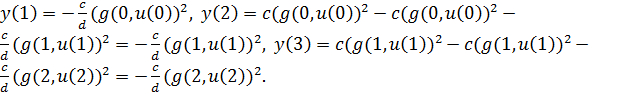
Отсюда .

Возможны три случая:

1) Если , то все управления оптимальны.

2) Если , то .

3) Если , то .

Пусть Составим функцию Понтрягина

и сопряженную систему

Решение сопряженной системы для любого имеет вид:

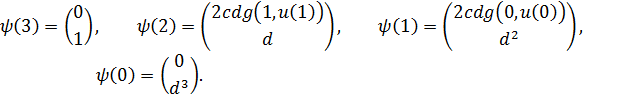Введем функцию

При

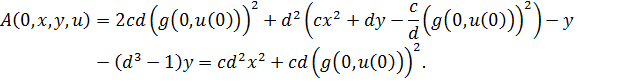
Если , то функция достигает минимума по при

Распишем при фиксированной

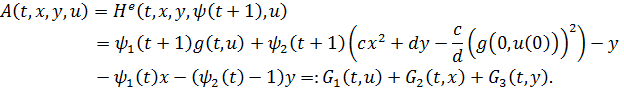
Получаем сумму трех функций от одного аргумента, причем выпукла по при , а линейна по (в переменные разделены). При этом

при , соответствующей произвольно фиксированному управлению , и двойственной траектории . Отсюда следует, что имеет минимум на любой паре . Аналогично, в силу сопряженной системы, т.е. не зависит от и, следовательно, тоже имеет минимум вдоль любой пары .

Остается рассмотреть

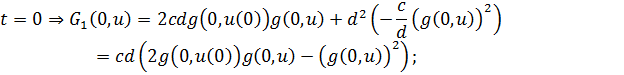
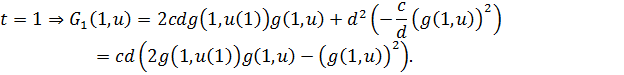
При аналогичное условие можно не рассматривать, т.к. при в задаче с вогнутой функцией условие минимума выполняется автоматически.

Из приведенного анализа следует, что при на любом допустимом процессе (в том числе и на оптимальных) функции и имеют при максимум по , а не минимум. Это означает, что условие минимума не является необходимым условием оптимальности в общих дискретных задачах оптимального управления.

Если же , то условие минимума выполняется на всех допустимых процессах, но достаточные условия (в терминах ) не выполняются, т.к. функция (или ) оказывается вогнутой по , а не выпуклой.

Проведем теперь схему улучшения неоптимального управления . Для заданного управления котраектория такова:

В зависимости от знака параметра , возможны два случая.

1) Пусть .

При

При

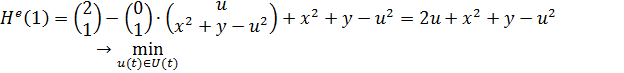
При

Отсюда получаем экстремальные селектора

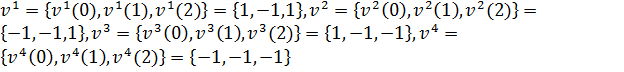
, которые образуют множество . Эти селектора дают оптимальные управления.

2) Пусть .

При

При

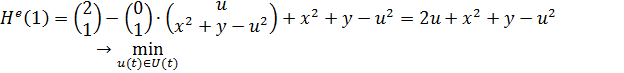
При

Отсюда получаем экстремальные селектора

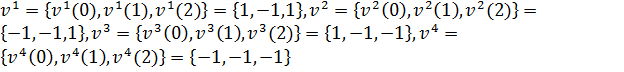
, которые образуют множество . Эти селектора дают оптимальные управления.

Можно видеть, что вне зависимости от знака параметра , схема улучшения неоптимального управления дает одно множество селекторов, которые доставляют оптимум функционалу.

В ходе данной работы было проведено аналитическое исследование негативного примера дискретной задачи оптимального управления. Сделан вывод о том, что схема улучшения неоптимального управления дает одно множество селекторов, которые доставляют оптимум функционалу. Попутно было установлено, что условие минимума не является необходимым условием оптимальности в общих дискретных задачах оптимального управления.

Литература:

1. Пропой А. И. Элементы теории оптимальных дискретных процессов.– М.: Наука. Гл. ред. физ.-мат. лит., 1973.

2. Иоффе А. Д., Тихомиров В. М. Теория Экстремальных задач.– М.: Наука, 1974.

3. Мордухович Б. Ш. Методы аппроксимаций в задачах оптимизации и управления.– М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 360 с.