Математика/1

Рашевський М.О.

Криворізький технічний університет

Асимптотичне інтегрування майже діагональних систем звичайних диференціальних рівнянь другого порядку

Розглянемо систему вигляду

(1)

де x(t, e) - шуканий n - вимірний вектор; A(t, e) – n´n - матриця, що зображується збіжним рядом за степенями дійсного малого параметра e > 0: 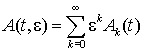, tÎ[0, L], L < ¥. Питання про асимптотичні розв’язки системи (1) вивчене у випадку стабільного спектра матриці A(t, e) [2] - [4]. Вимагалося виконання наступної умови.

1⁰. Коефіцієнти A_k(t) є нескінченно диференційовними на проміжку [0, L], k ³ 0.

У зв’язку з розв’язанням ряду прикладних задач система (1) розглядалась у [3] при наявності точок повороту (ТП) [1] – [3], тобто ізольованих точок, де збігаються принаймні два корені характеристичного полінома P(l, t, 0); , E - одинична матриця.

Розглядувана система може мати два типи ТП [3]: a) точка t = t₁ така, що l_i(t₁) = l_j(t₁) ¹ 0, i, j Î {1, 2, ¼, n}, i ¹ j, і l_i(t) ¹ l_j(t), якщо t ¹ t₁. b) точка t = t₂, де l_i(t₂) = 0 для деякого i Î {1, 2, ¼, n}, причому l_i(t) ¹ l_j(t) для i ¹ j, t Î[0, L]. Тут l_i(t) - корені полінома. Зокрема, у випадку виродження матриці A(t, e) у точці (0, 0) матимемо ТП t₂ = 0. При інтегруванні систем першого порядку із такою матрицею виникають так звані фазові ланцюги [1, 3], що є частинними розв’язками рівнянь вигляду де L( ) – функція, що виражається через відомі величини.

Продовжуючи дослідження [5], розглянемо задачу Коші

x(0) = x₀, ex¢(0) = x₁ (3)

для системи (1) у припущенні, що

2⁰. A(t, 0) подібна діагональній матриці L(t) = diag{l₁(t), l₂(t),¼, l_n(t)};

l_k(t) = tw_k(t), w_i(t) ¹ w_j(t) для i ¹ j, t Î[0, L]; T ^-1(t)A(t, 0)T (t) = L(t); det T (t) ¹ 0.

У такій постановці задача вміщує як окремий випадок задачу про накладання ТП, досліджену в [3]. За умов 1⁰, 2⁰ існує неособливе перетворення

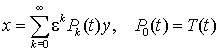(4)

таке, що зводить (1) до системи вигляду

e²y¢¢ + e²B(t, e)y¢ + A(t, e)y = 0 (5)

Записавши матриці B(t, e) та A(t, e) у вигляді B(t, e) = L₁(t, e) + B ^ij(t, e), A(t, e) = L₀(t, e) + A ^ij(t, e), де L₁(t, e) = d_ijB(t, e), B ^ij(t, e) = (1 - d_ij)B(t, e), будуватимемо розв’язок задачі Коші y(0) = y₀(e), ey¢(0) = y₁(e) для системи (5), і з урахуванням перетворень (4) одержимо розв’язок задачі (1), (3); .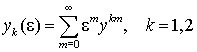

Формальний розв’язок системи (5) шукатимемо у вигляді

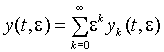(6)

Підставивши (6) у (5) та прирівнявши коефіцієнти при степенях e так, щоб для визначення y_k(t, e) дістати диференціальне рівняння [5], одержимо нескінченну систему:

e²y₀¢¢ + e²L₁y₀¢ - L₀y₀ = 0,

e²y₁¢¢ + e²L₁y₁¢ - L₀y₁ = eB₁^ijy₀¢ + A₁^ijy₀, (8)

e²y_k¢¢ + e²L₁y_k¢ - L₀y_k = .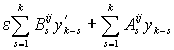

Задамо початкові умови: y₀(0) = y⁰⁰, ey₀¢(0) = y¹⁰, …, y_k(0) = y^0k, ey_k¢(0) = y^1k,…

Компоненти вектора y₀(t, e) знайдемо як розв’язки скалярних рівнянь

e²y₀¢¢_k + e²b_{k k} (t, e)y₀¢_k - l _k(t, e)y_0 k = 0.

Матимемо: y₀(t, e, C₀) = C₀₁y₀₁ + C₀₂y₀₂, де k – координати векторів y₀₁ та y₀₂ визначимо методами [2, 3] у вигляді

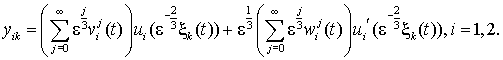
Тут u_i(t) – функції Ейрі [2, 3], 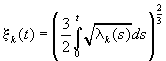. Розв’язок наступного рівняння системи (8) e²y₁¢¢ + e²L₁y₁¢ - L₀y₁ = eB₁^ijy₀¢ + A₁^ijy₀

побудуємо у вигляді 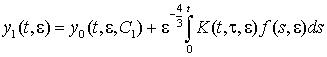, де , f (s, e) = eB₁^ijy₀¢ + A₁^ijy₀, а набір сталих C₁ здійснимо так, щоб задовольнити початкові умови (3). Зокрема, щоб виконати першу з умов, необхідно взяти .

Отже, при визначенні y₁(t, e) з’являються інтеграли від частинних розв’язків однорідного рівняння для визначення y₀(t, e).

Згідно з оцінками [2, 3] 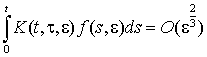. Звідси дістанемо для нульового наближення , що збігається із оцінкою [2]. Розв’язуючи далі систему (8) методом [2], переконаємось, що у виразах для y_k(t, e) матимемо інтеграли кратності k. Подібні інтеграли в [1] названі фазовими ланцюгами. Методом [2] при додатковій умові l_i(t) £ 0 на власні числа матриці A(t, 0) для m – наближення дістанемо оцінку:

(9)

Сформулюємо описаний спосіб побудови у вигляді наступного твердження.

Теорема. Якщо виконуються умови 1⁰, 2⁰, то задача (1), (3) має формальний розв’язок, утворений із (4), (6) такий, що отримане з нього m – наближення при l_i(t) £ 0 задовольняє нерівність (9).

Запропоновану методику без принципових змін можна застосувати до рівнянь вигляду 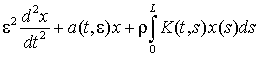, де r = e, тобто у випадку слабкого інтегрального збурення.

Література:

1. Кучеренко В.В. Асимптотика решения системы при h ® 0 в случае характеристик переменной кратности // Известия АН СССР, сер. Матем.-1974, 95, № 3.- C.625-662.

2. Ломов С.А. Введение в общую теорию сингулярных возмущений. – М.: Наука, 1981. – 400 с.

3. Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений.- М.: Наука, 1983. - 352 с.

4. Фещенко С.Ф., Шкиль Н.И., Николенко Л.Д. Асимптотические методы в теории линейных дифференциальных уравнений.- К.: Наук. думка, 1966. - 262 с.

5. Шкіль М.І., Рашевський М.О. Асимптотичне інтегрування лінійних систем другого порядку з нестабільним спектром.  // Доповіді НАН України, 2002. - № 3.- С. 39-43.