Коханенко В.Н., Папченко И.В., Папченко Н.Г.

Донской государственный аграрный университет

Формальное совпадение уравнений движения двухмерных в плане открытых водных потоков и уравнений движения идеального газа

В настоящее время в связи с развитием возможностей вычислительной техники и появлением мощных математических пакетов программ появилась возможность быстрого построения и апробирования различной сложности математических моделей по течению водных потоков. При этом наибольший интерес представляют собой наиболее простые модели, дающие, однако удовлетворительные по степени адекватности результаты для практики. Известно, что построение математической модели какого-либо физического процесса начинается с выбора системы уравнений, описывающей сам процесс. Часто математически формально система уравнений исследуемого процесса по внешнему виду сводится к уже известной системе, решение краевых задач, на базе которой также известно и его можно заимствовать для решения новой исследуемой задачи.

Целью настоящей работы является приведение известных уравнений движения идеального газа и уравнений движения, двухмерных в плане открытых водных потоков, при определенных ограничениях на поток к сопоставимому виду и демонстрации их совпадения.

Рассмотрим вначале уравнения движения двухмерных в плане открытых водных потоков. Для этого воспользуемся в качестве исходной системы известной системой двухмерных в плане уравнений движения открытого водного потока в случае горизонтального плоского отводящего русла, в которой не учитываются силы трения потоку [1]:

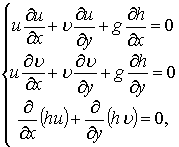(1)

где - осредненные по глубине потока проекции местной скорости;

- местная глубина потока;

Оху – плоская прямоугольная декартова система координат (в плоскости течения потока);

Ох – продольная ось симметрии потока;

Оу – дополняет ось Ох до правой системы координат;

- ускорение силы тяжести.

Система уравнений в частных производных (1) является, в соответствии с общепринятой в математической литературе [2] классификацией, существенно нелинейной системой, и поиск ее регулярных решений представляет определенные трудности. Поэтому для ее упрощения примем дополнительные условия, а именно потенциальность потока, т.е. существование функции такой, что выполнялись бы равенства:

(2)

Линия называется эквипотенциальной. Тогда с учетом условий (2) система уравнений (1) трансформируется к виду:

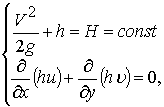(3)

где ; а постоянная «Н» определяется, если известны модуль

вектора скорости - и глубина потока - в некоторой характерной его

точке по формуле: .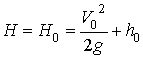

Первое уравнение системы (3) представляет собой интеграл Бернулли для двухмерных в плане водных потоков. Второе уравнение системы (3) является уравнением неразрывности потока и определяет существование функции тока , такой, что выполняются равенства:

(4)

Линия (5) называется линией тока, которая обладает свойством непроницаемости потока вдоль нее. Из условия (5) следует:

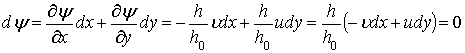, (6)

т.е. , . (7)

Условие (7) показывает, что касательная к линии тока совпадает с направлением вектора скорости жидкой частицы в рассматриваемой точке потока (рис.1).

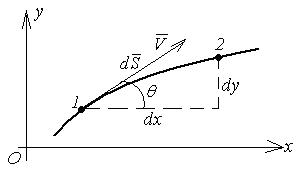
Рис. 1. Схема к пояснению понятия линии тока.

При совпадении направления векторов и выполняется условие: , (8)

из которого следует условие (7).

Линии тока перпендикулярны эквипотенциалам в физической плоскости. Это следует из условия:

.

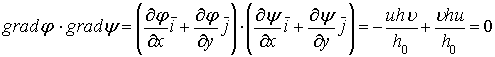Итак, систему уравнений (2), (3), (4) будем считать базовой для двухмерных в плане открытых водных потоков. Перепишем ее еще раз для лучшего восприятия по тексту работы:

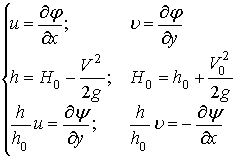(9)

Введем понятие квадрата скоростного коэффициента 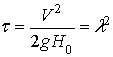(10) и преобразуем систему (9) к виду:

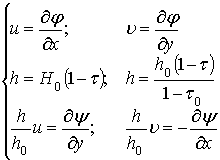(11)

Из системы (11) получим зависимость между функциями и , характеризуемую формулами:

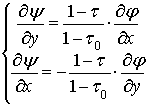(12)

Преобразуем далее систему (12), переходя в плоскость годографа скорости, т.е. к переменным [3]. В результате получим систему:

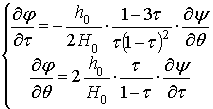(13)

Для удобства введем новую функцию тока 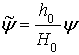(14) отличающуюся от постоянным множителем . В результате система (13) преобразуется к виду:

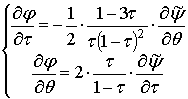(14)

Или убирая волну над в системе (14) окончательно получим систему уравнений двухмерных в плане потоков в плоскости годографа скорости в виде:

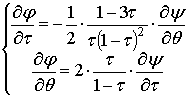(15)

Системе (15) эквивалентно уравнение в частных производных второго порядка: 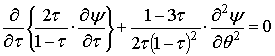. (16)

Для спокойных потоков ; (17)

для бурных потоков . (18)

Уравнения (15), (16) решают вопрос о течении жидкости, если известна область переменных , соответствующая этому течению, если даны значения на граничных линиях тока; если везде, внутри области, функция вместе со своими первыми производными конечна, однозначна и непрерывна, а количество не превышает и обращается в нуль лишь в некоторых точках контура для спокойных потоков и превышает и обращается в единицу лишь в некоторых точках контура для бурных потоков. Для спокойных потоков уравнение (16) относится к эллиптическому типу. Оно переписывается в раскрытом виде:

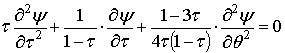. (19)

Из сравнения уравнения (19) с уравнением общего вида

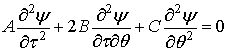[2] видно, что , ,

и , при , (20)

и уравнение (19) относится к эллиптическому типу.

Далее рассмотрим идеальный газ. Потенциальное движение газа согласно [4] требует для адиабатного процесса выполнение равенства:

, т.е. , (21)

где - давление газа;

- коэффициент пропорциональности;

- показатель адиабаты;

- плотность газа.

А.С. Чаплыгин рассматривал движение газа с сохранением тепла частицами газа ввиду малой теплопроводности и малой лучеиспускательной способности газа.

Для потенциала скоростей имеем функцию :

, . (22)

Уравнение неразрывности записывается в виде:

. (23)

Закон Бернулли с использованием уравнения (21) приводит к соотношению: 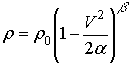, (24)

где , , , .

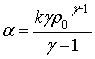При этом плотность газа в точке с . Полагая 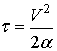[4] из (24) получим: . (25)

В литературе [5] эта же формула приводится в виде 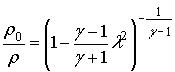. Из уравнения (23) следует существование функции , определяемой равенствами:

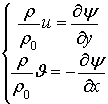(26)

Далее, переходя в плоскость годографа вектора скорости, получим уравнения С.А. Чаплыгина для идеального газа [4] в виде:

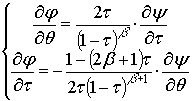(27)

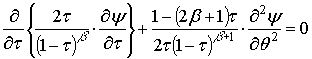. (28)

С.А. Чаплыгин в своих исследованиях рассматривал случай дозвукового течения совершенного газа и разработал методы решения ряда практических задач по течению идеального газа при его дозвуковых режимах.

Как видно из сравнения уравнений (15), (16) и (27), (28) они совпадают при . Следовательно, в плоскости годографа вектора скорости при одних и тех же граничных условиях решения соответствующих задач для газа при и двухмерного в плане спокойного потока будут совпадать. Этот факт дает широкие перспективы для теории и практического развития аналитических решений граничных задач по течению двухмерных в плане открытых водных потоков. Он позволит хорошо разработанные методы моделирования в газовой динамике заимствовать для решения сопоставимых задач по течению двухмерных в плане открытых водных потоков.

В заключение работы приведем для интересующихся исследователей формулу, связывающую параметры потока в плоскости годографа скорости жидких частиц с параметрами потока в физической плоскости течения потока в дифференциальном виде:

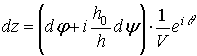, (29)

где , позволяющую имея решение граничной задачи в плоскости перейти в плоскость , т.е. полностью решить соответствующую задачу.

Литература

1. Емцев Б.Т. Двухмерные бурные потоки [Текст]/ Б.Т. Емцев. – М.: Энергия, 1967. – 212 с.

2. Справочник по математике для научных работников и инженеров / Под общ. ред. Г. Корн, Т. Корн. – М.: Наука, 1970. – 720 с.

3. Коханенко В.Н. Моделирование одномерных и двухмерных открытых водных потоков / В.Н. Коханенко, Я.В. Волосухин, В.В. Ширяев, Н.В. Коханенко: под общей ред. В.Н. Коханенко. – Ростов н/Д: Изд-во ЮФУ, 2007. – 168 с.

4. Чаплыгин С.А. Избранные труды. Механика жидкости и газа. Математика. Общая механика. [Текст] / С.А. Чаплыгин. – М.: Наука, 1976. – 496 с.

5. Лойцянский Л.Г. Механика жидкости и газа [Текст] / Л.Г. Лойцянский. - 5-е изд. М.: Наука, 1978. – 736 с.