Математика / 5. Математическое моделирование

К.ф.-м-н. Быкова И.Ю.

Восточно-Казахстанский государственный технический университет, Республика Казахстан

Модель принятия решения в условиях неполной информации с априорными решающими правилами

В процессе управления обычно представляется возможность последовательно наблюдать реализации случайных параметров условий задачи и каждый раз, если это окажется целесообразным в соответствии с вновь накопленной информацией, корректировать решение. Предварительный план и последовательные корректировки должны, конечны, помимо содержательных ограничений, учитывать априорные характеристики случайных параметров условий на каждом этапе. Последовательность поступления информации и порядок выбора и корректирования решения определяется информационной структурой задачи – набором исходных данных, накопленных на предшествующих этапах, от которого может зависеть решение на текущем этапе.

Если решение предшествует наблюдению, то оптимальный план стохастической задачи определяется статистическими характеристиками или известной выборкой возможных значений параметров условий задачи. Решения будем вычислять в чистых стратегиях с учетом априорной информации – некоторых характеристик распределения или выборок возможных значений случайных параметров условий.

Будем рассматривать многоэтапную задачу принятия решений в условиях неполной информации с априорными решающими правилами. В качестве критерия оптимальности принцип выбора пропорционального развития экономики региона:

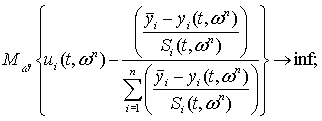(1)

(2)

(3)

(4)

, (5)

где t Î[1,T] – периоды принятия решения по распределению информационных ресурсов; c(t) = j(t) + y(t) – определенное количество имеющихся информационных ресурсов системы, причем j(t) – ресурсы, подлежащие распределению в данный момент времени t, y(t) – ресурсы, направляемые в резерв информационной системы, которые могут быть использованы в некоторый момент времени t Ì[1,T]; i = 1,2, ..., n – возможные варианты распределения информационных ресурсов; n – количество возможных вариантов распределения имеющихся информационных ресурсов; u_i(t) – количество ресурсов, вкладываемых в i-й вариант распределения в момент времени t; y_i(t) – показатель функционирования системы при использовании i-го варианта распределения ресурсов в момент времени t; – экспертные оценки (некоторое числовое выражение) идеального или желательного уровня функционирования системы при использовании i-го варианта распределения ресурсов; S_i(t) – эффективность использования i-го варианта распределения информационных ресурсов в момент времени t.

Обозначим нижнюю грань показателя качества решения данной задачи принятия решения через т.е. .

Пусть решение на i-м этапе принимается после реализации случайных параметров условий на предыдущем i–1-ом этапе, тогда решающие правила имеют вид:

Задача (1)-(5) – многоэтапная задача стохастического программирования с условными вероятностными ограничениями и с априорными решающими правилами.

Для пояснения постановки задачи опишем вспомогательные формальные понятия. Пусть w_i ÎW_i, i = 1,2, ..., n, где W_i – некоторые множества – пространства элементарных событий w_i на i-м этапе; W₀ = {w₀}; w ⁱÎW ⁱ = W₁´W₂´¼´W_i; w ⁱ = (w₁,w₂,¼,w_i) – вектор в пространстве размерности i; w ⁿÎW ⁿ = W₁´W₂´¼´W_n; w ⁿ = (w₁,w₂,¼,w_n) – последовательность случайных событий.

Пространство случайных событий W ⁿ обозначим через W (W ⁿ = W ).

Пусть на W задана вероятностная мера P. Определим меру P ^k на W ^k следующим образом: если элементарное событие AÌW ^k, тогда P ^k(A) = P(A´W_k+1´W_k+2´¼´W_n). Введем условную вероятностную меру P_k на W_k:

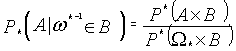для любого , S –s - алгебра случайных событий на W. Таким образом, мы определили вероятностное пространство (W, S, Р).

Рассмотрим последовательность множеств Y₀, Y₁, ..., Y_n произвольной структуры, y_kÎY_k, k = 0,1, ..., n;

Y₀ = {y₀(t)};

Y^k = Y₁´Y₂´¼´Y_k, y^k = (y₁(t),y₂(t), ..., y_k(t));

Yⁿ º Y

Пусть для каждого w^kÎW^k и y_i^k(t)ÎY^k, k = 1,2, ..., n задана вектор-функция y_k(w^k,y_i^k(t)) размерности m_k; на множестве Y для каждого wÎW функционал y₀(wⁿ,y_iⁿ(t)); G_k⁰ = G_k⁰(w^k) – некоторые случайные множества; c_k(t,w^k-1) –

m_k-мерные случайные величины – ограниченные измеримые вектор-функции от w^k-1; c^k(t,w^k-1) – -мерная вектор-функция; c^k(t,w^k-1) ÎB_k, B_k – некоторое банахово пространство; – условное математическое ожидание u_i(t,w^k) в предположении, что известна реализация w ^k-1.

Сформулируем задачу i-го этапа.

Рассмотрим множество, отвечающее области определения задачи i-го этапа для задачи (1)-(5) при фиксированных w ^i-1 и u^i-1:

(6)

(7)

. (8)

Сформулируем необходимое и достаточное условие разрешимости задачи (1)-(5).

Теорема 1. Если целевая функция задачи (1)-(5) ограничена снизу, то для разрешимости задачи (1)-(5) необходимо и достаточно, чтобы выполнялось условие K₁¹Æ.

Запишем целевую функцию Q_i(y_i,i(t)) задачи i-го этапа.

где

– набор случайных параметров, реализованный на этапах, предшествующих этапу i;

– набор принятых решений;

– решение на этапе i;

– оптимальное решение на этапах, следующих за i-м;

Определение оптимального решающего правила на i-м этапе многоэтапной стохастической задачи сводится, таким образом, к решению задачи математического программирования:

(9)

При сепарабельной целевой функции

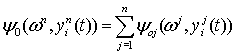(10)

вычисление упрощается.

Пусть

При сепарабельной целевой функции оптимальное решающее правило задачи (1)-(5) удовлетворяет на каждом этапе i=1,2,...,n-1 следующему функциональному уравнению Беллмана:

(11)

при i = n

(12)

из (10)-(12) следует, что

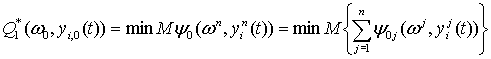(13)

при условиях (2)-(5).

Таким образом, задача (1)-(5) в предположении (10) эквивалентна задаче (11)-(13).

Целевая функция i-го этапа имеет в этом случае вид :

(14)