О
функциональном строении бинарных операций
к.ф.-м.н. доц. В.И.
Евсеев
![]()
Казанский институт
социальных и гуманитарных знаний,
Казань, Россия,
кафедра прикладной информатики
УДК 681.32 1 - vladislaw.evseev@yandex.ru,
Модель
адаптированной логической системы
Аннотация:
Данная работа посвящена моделированию структуры
бинарных логических операций для случая модели «мягкой логики», в которой
определяются специфические значения арифметической функции истинности.
Построена авторская модель конъюнкции в этой модели и указаны
возможности построения других бинарных операций.
This work is devoted to modeling the structure of
binary logic operations for the case of "soft" logic model that
identifies the specific values of an arithmetic function. Is the author's model of a conjunction in
this model and the possibility of building other binary operations.
Ключевые
слова:
«Мягкая»
логическая система, основное уравнение логики, отделяющие функции семантических
классов, определение значений функций истинности бинарных операций.
1. Структура «мягкой» логической системы.
В одной из своих публикаций (см. ![]() (стр.
278)), мы уже касались методики
построения логики по интуиционистскому принципу. Для него характерно неточное
задание значений функции истинности, что и принято называть «мягкой» логической
системой. Если «мягкая» логическая
система
(стр.
278)), мы уже касались методики
построения логики по интуиционистскому принципу. Для него характерно неточное
задание значений функции истинности, что и принято называть «мягкой» логической
системой. Если «мягкая» логическая
система ![]() строится
на базе классической двузначной логики,
то значения истинности выбираются следующим образом:
строится
на базе классической двузначной логики,
то значения истинности выбираются следующим образом: ![]() - параметр,
соответствующий относительно ложному суждению,
- параметр,
соответствующий относительно ложному суждению, ![]() - параметр, соответствующий относительно истинному
суждению (
- параметр, соответствующий относительно истинному
суждению (![]() ).
).
При этом
основное уравнение логики имеет вид:
![]() ,
(1.1)
,
(1.1)
где ![]() - текущее арифметическое значение логической
переменной.
- текущее арифметическое значение логической
переменной.
Указанная в
цитируемом источнике методика
позволяет найти отделяющие функции классов истинности этой модели:
![]()
![]() ,
(1.2)
,
(1.2)
![]() .
(1.3)
.
(1.3)
Следствиями из основного
уравнения (1.1) являются свойства:
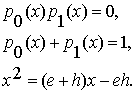 (1.4)
(1.4)
Первое из этих
соотношений указывает, что классы истинности в данном универсуме не
пересекаются. Второе говорит о том, что эти классы полностью покрывают весь
универсум. В результате можно заметить, что построено его правильное покрытие.
Третья формула позволяет утверждать, что все логические уравнения с одной
переменной будут линейными, а с двумя переменными будут квадратичными формами (без участия квадратов каждой
переменной).
2. Теперь универсум данной логической системы ( ![]() ) можно представить в виде прямой суммы двух
непересекающихся классов истинности:
) можно представить в виде прямой суммы двух
непересекающихся классов истинности:
![]() =
=![]()
![]() .
(1.5)
.
(1.5)
Выберем логически значащие части
суждения ![]() ,
принадлежащие заданным классам истинности:
,
принадлежащие заданным классам истинности:
![]() и
и
![]() . При этом само
высказывание
. При этом само
высказывание ![]() имеет
структуру:
имеет
структуру:
![]() .
(1.6)
.
(1.6)
Отсюда сразу же следует
формула для его структурной симметрии:
![]() .
(1.7)
.
(1.7)
Введем теперь функцию
истинности суждения по условиям:
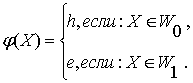
![]() (1.8)
(1.8)
Таким образом, из формул
(1.6) и (1.7) получим:
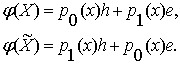 (1.9)
(1.9)
3. Если теперь
подставить в эти формулы значения отделяющих функций из (1.2) и (1.3), то
найдем, во-первых, естественное выражение для исходной функции:
![]() =
= ![]() ,
(1.10)
,
(1.10)
а во-вторых, явное
значение функции истинности структурной
симметрии:
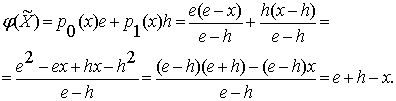 (1.11)
(1.11)
Таким образом, мы нашли
основные формулы для двузначной «мягкой» логической системы.
2. Изучение стандартной конъюнкции (в логике ![]() ).
).
1.Для
изучения конъюнкции введем второе суждение
![]() (2.1)
(2.1)
А также его
структурную симметрию
![]() (2.2)
(2.2)
Стандартная конъюнкция
определяется исходно простой формулой:
![]() (2.3)
(2.3)
Матричное задание этой
бинарной операции имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
На основе
этой матрицы можем построить выражение
для ее операции:
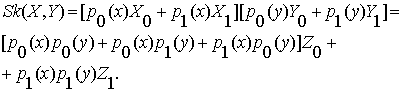 (2.4)
(2.4)
Значит, для конъюнкции
получаем функцию истинности в логике ![]()
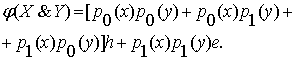 (2.5)
(2.5)
Поэтому матрица
истинности конъюнкции такова:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
Такая
таблица может быть построена для каждой бинарной операции, а с ее помощью
находится явное выражение функции истинности для любой из этих операций (мы
оставляем за этой формулой ее традиционное название).
2.Теперь из формулы (2.5) получаем явное выражение функции истинности:
![]() (2.6)
(2.6)
Позволим себе не приводить все соответствующие
вычисления.
Покажем на этом примере, как в реальности работают функции
истинности. Для этого вычислим по формуле (2.2.6) значения этой функции на
конкретных классах истинности исходных аргументов:
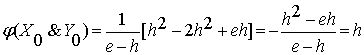 , (2.7)
, (2.7)
![]() , (2.8)
, (2.8)
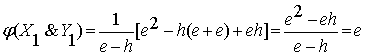 . (2.9)
. (2.9)
Эти
результаты однозначно соответствуют матрице истинности (см. табл. 1, ряд 1).
Поэтому получаем формулу для функции классов этой конъюнкции:
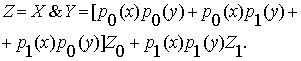 (2.10)
(2.10)
Аналогичные формулы получаются и для других бинарных операций.
3.
Моделирование значений бинарных операций
Два взаимных поляроида определяются традиционно
как соответствующие разности конгруэнций, поэтому для них можно получить:
для левого поляроида:
![]() (3.1)
(3.1)
По аналогии для правого поляроида сразу запишем
результирующую формулу функции истинности:
![]() . (3.2)
. (3.2)
Нильюнкция и дизъюнкция
представляют собой две соинверсных бинарных операции, причем первая из них
является конъюнкцией двух отсимметрированных ранее суждений:
![]() , (3.3)
, (3.3)
а вторая операция
представляет ее внешнюю структурную
симметрию:
![]() . (3.4)
. (3.4)
Учитывая
формулу (1.11), получим:
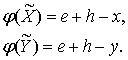 (3.5)
(3.5)
Отсюда
непосредственно следует:
![]()
После небольших преобразований получим окончательный
результат:
![]() (3.6)
(3.6)
Теперь для дизъюнкции, как внешней структурной симметрии
нильюнкции, получаем:
![]() . (3.7)
. (3.7)
Теперь
перейдем к изучению взаимных импликаций.
Левая
импликация имеет представление:
![]() (3.8)
(3.8)
Значит, для
ее функции истинности имеем:
![]() ,
,
Что после
небольших преобразований дает результат:
![]() . (3.9)
. (3.9)
Для правой
импликации по аналогии получаем:
![]() (3.10)
(3.10)
Значит,
формула для ее функции истинности такова:
![]() . (3.11)
. (3.11)
Эквиваленция
– это операция третьего уровня, как и ее структурная симметрия, называемая нами
хартъюнкцией (старое название «строгая дизъюнкция»). Для эквиваленции получаем
определяющую матрицу классов:
|
|
|
|
|
|
|
|
|
|
|
|
![]() =
=
Отметим, что
эквиваленция является конъюнкцией двух взаимных импликаций:
![]() . (3.12)
. (3.12)
Согласно таблице значений, получим общую
формулу эквиваленции:
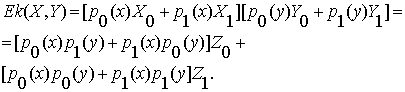
Применив
функцию истинности, находим:
 (3.13)
(3.13)
Проведя
соответствующие преобразования, находим формулу для этой операции:
![]() .
(3.14)
.
(3.14)
Учитывая, что
хартъюнкция – это взаимная операция к
изученной уже эквиваленции, получим:
![]() . (3.15)
. (3.15)
Формула для
ее функции истинности получается почти сразу же:
![]() (3.16)
(3.16)
Штокъюнкция, как операция, взаимная с конъюнкцией, имеет
следующую функцию истинности:
![]() . (3.17)
. (3.17)
Таким образом, мы
рассмотрели все основные бинарные операции в «мягкой» модели логики и нашли для
них функции истинности.
Литература:
1. Евсеев В.И. Основы
аналитической семантики. Монография. Издательство «Lambert», 2014 г.( 168 стр.)
2. Евсеев В.И., Вафин Ф.Ф. Информационное
обоснование логической семантики //Теория и технология компьютерного обучения,
вып. 6. Изд – во КГТУ (КАИ). 2002 (3- 16).
3. Евсеев В.И. О логических
основах функционирования систем// Труды ![]() Всероссийской научной
конференции «Информационные технологии в системе социально-экономической
безопасности России и ее регионов». Казань. 2010 (278 – 281).
Всероссийской научной
конференции «Информационные технологии в системе социально-экономической
безопасности России и ее регионов». Казань. 2010 (278 – 281).
Сведения об авторе:
Автор
– Евсеев Владислав Иванович, кандидат физико-математических наук, доцент
Казанского (Приволжского) федерального университета, кафедра прикладной
информатики.
Год
рождения: 1946.
Стаж:
44 года.
Опубликовано
всего – более 100 научных и методических работ, в том числе 3 монографии.
С
уважением.
Евсеев
В.И.