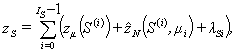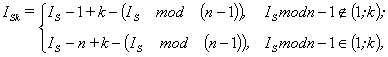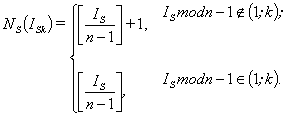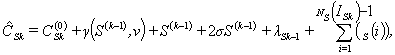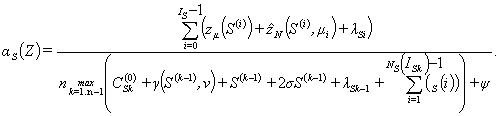Математика / 4. Прикладная математика.
к.т.н. Крючин О.В.
Тамбовский государственный
университет им. Г.Р. Державина, Россия
Аналитическая
модель для информационного процесса выбора структуры многослойного персептрона с
использованием параллельных вычислений
Как показано
в работах [1-3], информационный процесс выбора структуры искусственных
нейронных сетей (ИНС) организован следующим образом:
1. определение начальной
структуры сети;
2. подбор активационных
функций и весовых коэффициентов;
3. проверка критерия остановки
обучения; если критерий выполняется, то завершение подбора (в качестве критерия
могут выступать временные затраты, требуемая точность и т.п.);
4. проверка возможности
добавления нового нейрона на последний скрытый слой (в качестве критерия может
использоваться максимально допустимое количество нейронов на слое,
минимально-допустимая разница между текущим и предыдущим значениями невязки и
т.п); если нейроны добавлять можно, то добавляется новый и переход к пункту 2;
5. проверка возможности
добавления нового слоя; если добавить новый слой возможно, то он добавляется;
переход к пункту 2 [4].
В отличие от
многослойного персептрона, где каждый скрытый слой может иметь произвольное
количество нейронов, в каскадной сети и сети Вольтерри количество нейронов на
каждом из слоев определяется однозначно [5]. В случае каскадной сети каждый
скрытый слой содержит только один нейрон, а в структуре Вольтерри количество
нейронов на 
-ом слое выражается формулой
|
|
(1) |
где 
— количество
слоев. Следовательно, упростив описанный выше информационный процесс выбора
структуры (убрав из него подбор числа нейронов в каждом из скрытых слоев), его
можно применить для этих типов структур.
При
повышении эффективности информационных процессов (с помощью параллельных
вычислений) выбора структуры
используются 
элементов
информационных ресурсов (ИР-элементов). Под ИР-элементами здесь понимаются узлы
кластерной системы или компьютеры распределенной вычислительной сети. Ведущий
ИР-элемент формирует структуры и посылает на остальные. Получив структуру ИНС,
ИР-элементы начинают подбор весовых коэффициентов (и при необходимости типов
активационных функций). После того, как какой-либо ИР-элемент заканчивает
обучение, он посылает обученную структуру ведущему, который проверяет
необходимость продолжать обучение. Если такая необходимость остается, он
формирует новую структуру и вновь посылает ее свободному ненулевому
ИР-элементу. Такой процесс продолжается до тех пор, пока не будет подобрана
структура, которая удовлетворяет необходимым условиям [4].
Для
построения аналитической модели, обозначим количество элементов исходной
структуры ИНС как 
, тогда после добавления одного скрытого нейрона количество
элементов становится равным 
, после добавления второго — 
и т.д. Значения 
зависят от типа
структуры сети. Таким образом, учитывая, что на каждой итерации необходимо
добавить нейрон, провести подбор активационных функций и проверить ИНС на
адекватность, в случае, когда для подбора структуры сети необходимо перебрать 
вариантов, количество
операций может быть выражено формулой
|
|
(2) |
где 
— количество
операций, которое необходимо для добавления нейрона 
в 
-ую структуру, 
— к-во операций,
необходимых для подбора активационных функций (и весовых коэффициентов) сети в 
-ой структуре, 
— к-во операций,
необходимых для проверки критерия остановки обучения при 
-ой структуре.
В
случае параллельного информационного подбора структуры каждый ИР-элемент
подбирает активационные функции (и весовые коэффициенты) самостоятельно [2]. В
этом случае 
-ый ИР-элемент для обучения одной структуры затрачивает 
операций, а поскольку
он выполняет операции для получения и отправки этой структуры (
) , а также ожидание формирования (
), то общее количество операций вычисляется по формуле
|
|
(3) |
Таким
образом, ведущий ИР-элемент при первом проходе осуществляет 
операций:
|
|
(4) |
(
— обучение структуры 
-ым ИР-элементом, 
— возвращение
обученной структуры, 
— получение структуры
ведущим ИР-элементом, 
— проверка сети на
адекватность).
Поскольку
значение 
обычно превосходит
количество ИР-элементов 
, то 
-ый ИР-элемент последовательно обучает структуры с номерами 
, 
, 
, 
, 
, 
, 
. Номер последней структуры 
, обучаемой 
-ым ИР-элементом, вычисляется по формуле (5), а количество
структур 
— по формуле (6).
|
|
(5) |
|
|
(6) |
Таким
образом, количество операций, осуществляемых 
-ым ИР-элементом (включая пустые), можно вычислить по формуле
|
|
(7) |
|
|
(8) |
Соответственно, общее
количество операций 
вычисляется по
формуле
|
|
(9) |
где 
— задержки,
возникающие из-за асинхронности процесса, а коэффициент эффективности — по
формуле
|
|
(10) |
Таким
образом, аналитическая модель для информационного процесса выбора структуры многослойного
персептрона с использованием параллельных вычислений может быть выражена
формулой
|
|
(11) |
Литература:
1.
Крючин О.В., Арзамасцев А.А., Королев
А.Н., Горбачев С.И., Семенов Н.О. Универсальный симулятор, базирующийся на
технологии искуственных нейронных сетей, способный работать на параллельных
машинах / О.В. Крючин [и др.] // Тамбов: Вестн. Тамб. ун-та. Сер. Естеств. и
техн. науки. 2008. – Т.13, Вып. 5. – C. 372-375.
2.
Универсальный
программный комплекс для компьютерного моделирования на основе искусственной
нейронной сети с самоорганизацией структуры / А.А. Арзамасцев [и др.] // Вестн.
Тамб. Ун-та. Сер. Естеств. и техн. науки,
2006. — Т. 11,
Вып. 4. — C. 564-570.
3.
Крючин О.В. Алгоритм самоорганизации
структуры искусственной нейронной сети для параллельных машин. // В мире
научных открытий №2 (08). Часть 3. 2010. —
Красноярск, 2010. с. 28-30.
4. Крючин О.В.
Подбор архитектуры искусственных нейронных сетей с использованием кластерных
систем // Электронный журнал "Исследовано в России", 115, стр.
1510-1523, 2009 г. // Режим доступа: http://zhurnal.ape.relarn.ru/articles/2009/115.pdf , свободный. - Загл. с экрана.
5. Осовский C. Нейронные сети для обработки информации =
Sieci neuronowe do przetwarzania informacji
(польск.) / Перевод И. Д. Рудинского. — М.: Финансы и статистика, 2004.
— 344 с. — ISBN 5-279-02567-4