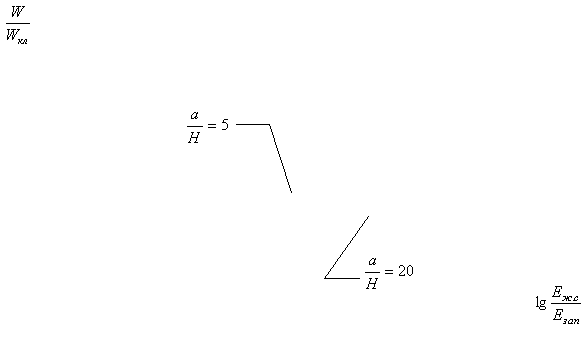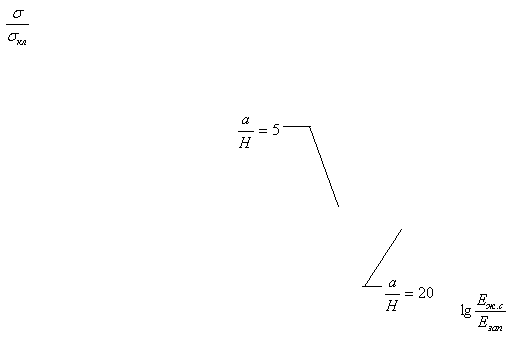Технические науки/ 2. Механика

УДК 539.3:534.1

К.т.н. Мутовина Н.В., Куанышев Т.Т.

Карагандинского государственного технического университета, РК, г.Караганда

ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПРЯМОУГОЛЬНЫХ МНОГОСЛОЙНЫХ ПЛАСТИН

Расчет слоистых пластин в трехмерной постановке представляет сложную задачу строительной механики, тем не менее, известен ряд задач, решенных в рамках трехмерной теории упругости. В условиях работы они оказываются наиболее рациональными с точки зрения обеспечения минимума весовых показателей при требуемой прочности и жесткости. Но они не всегда удовлетворяют всем требованиям, предъявляемым к строительным конструкциям и элементам современной техники приходится использовать многослойные конструкции. Теории многослойных пластин, уточняющие техническую теорию, должны учитывать деформацию в поперечном направлении и связанные с нею факторы. Проведено численное исследование напряженно-деформированного состояния многослойных пластин на основе метода сеток. Полученные уравнения изгиба многослойных ортотропных пластин несимметричной структуры по толщине в смешанной форме и соответствующие им контурные условия представлены в конечно-разностной форме для произвольного узла прямоугольной сетки.

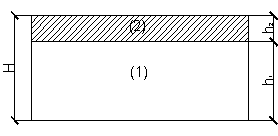
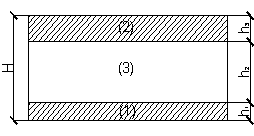
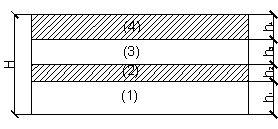
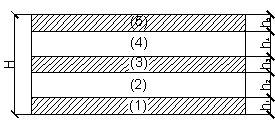
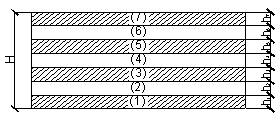
Исследуем напряженно-деформированное состояние многослойных пластин с различным количеством и расположением слоев по толщине, симметричной и несимметричной структуры [1]. Пластины – квадратные в плане, свободно опертые по контуру, действующая нагрузка равномерно-распределенная [2]. Рассматриваемые пластины имеют равную массу, т. е. для всех пластин суммарные толщины несущих слоев и слоев заполнения соответственно одинаковы (рисунок 1).

В процессе расчета варьировались отношения: модуля упругости жестких несущих слоев и заполнителя , размера пластин в плане к ее общей толщине . Шаг сетки при решении всех задач принят равным [3].

Для слоев приняты следующие жесткостные характеристики:

Е_ж.с= 7×10⁴МПа; Е_зап=Е_ж.с/100;

ν_ж.с=0,3; ν_зап=0,4.

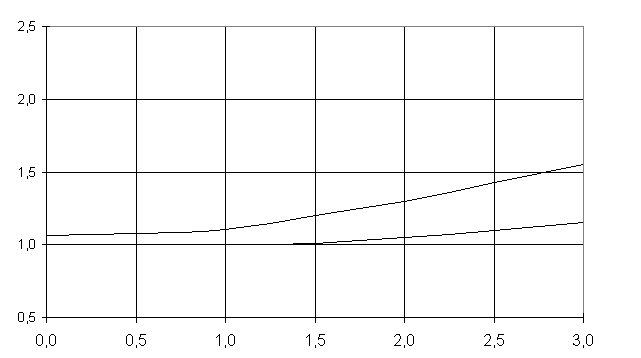
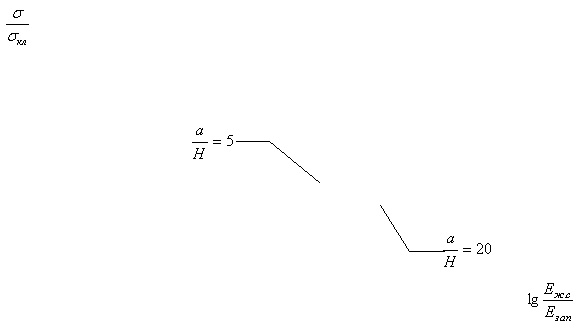
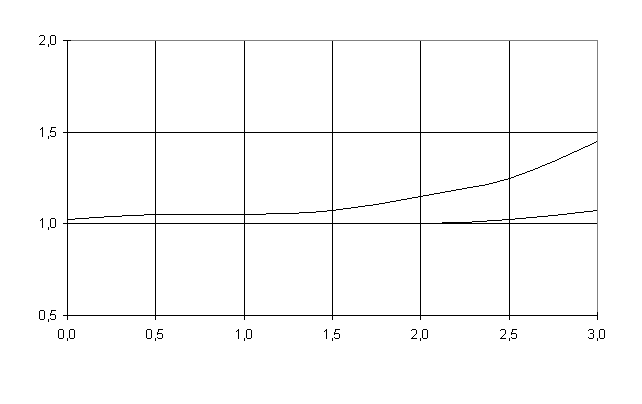
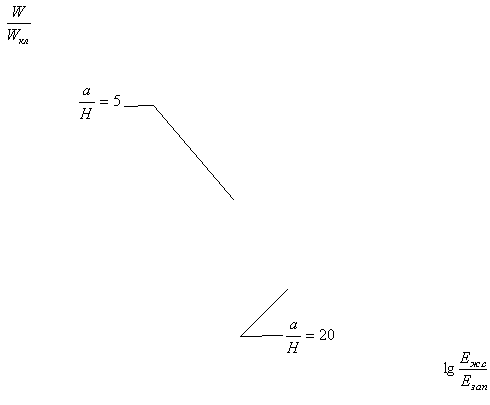
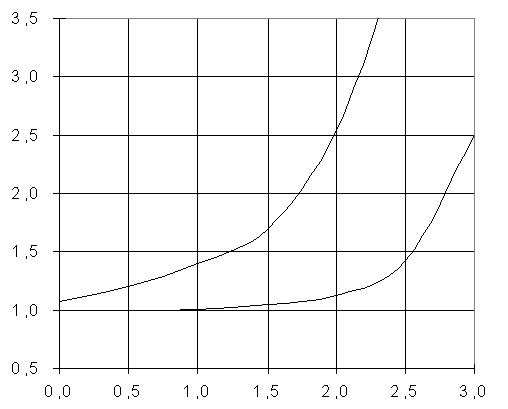
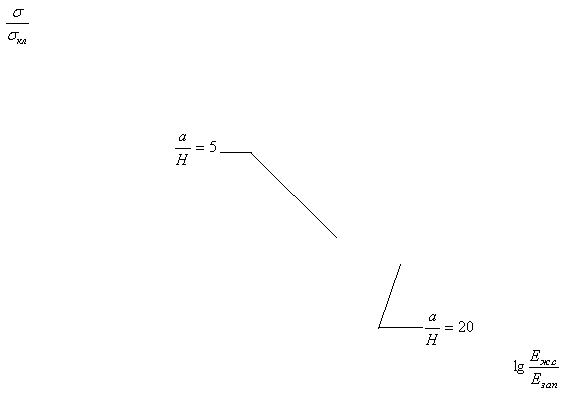
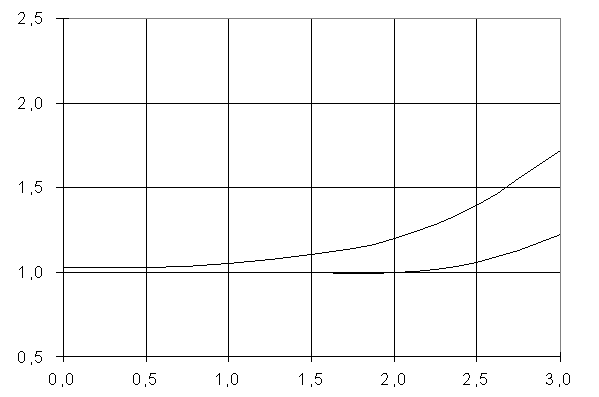
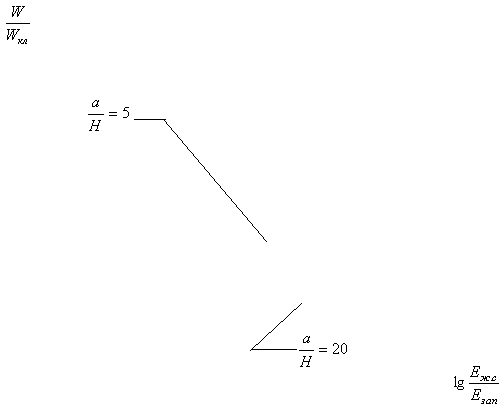
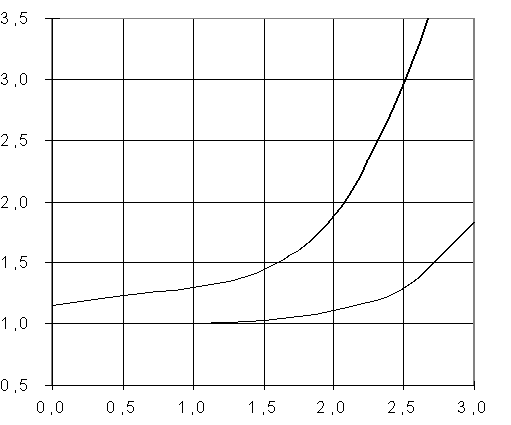
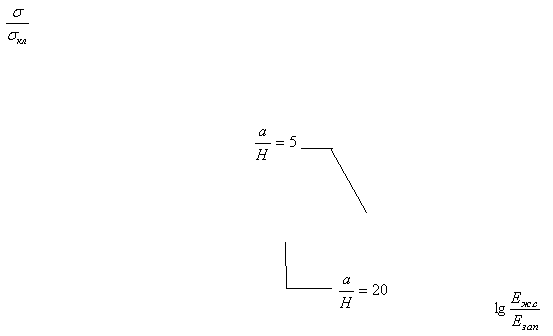
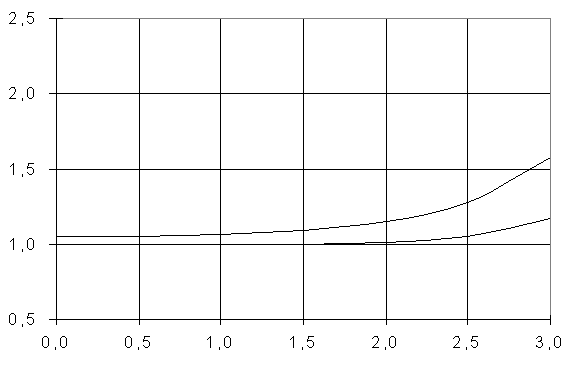
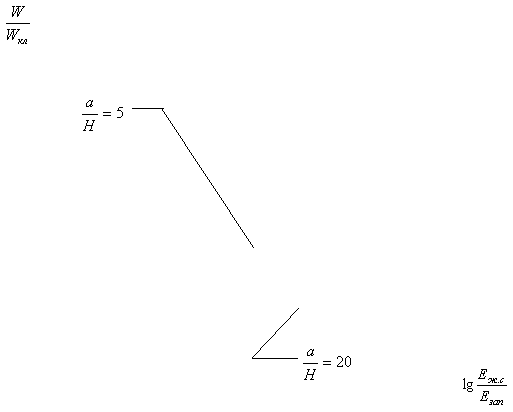
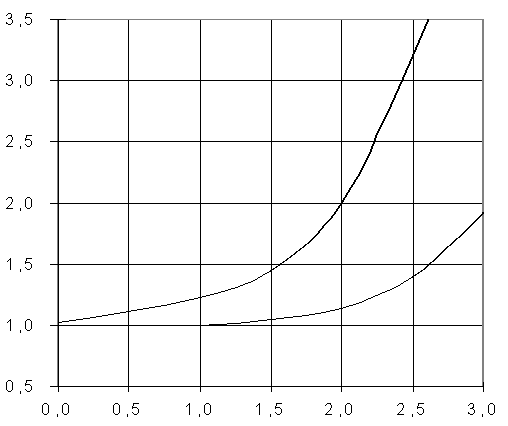
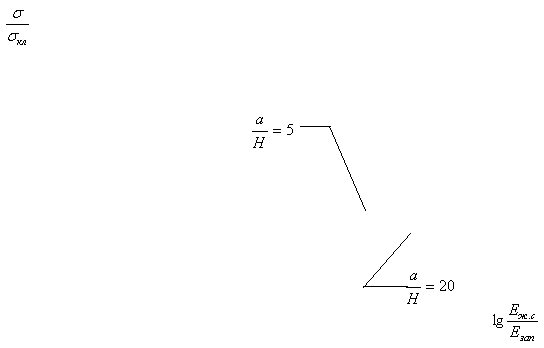
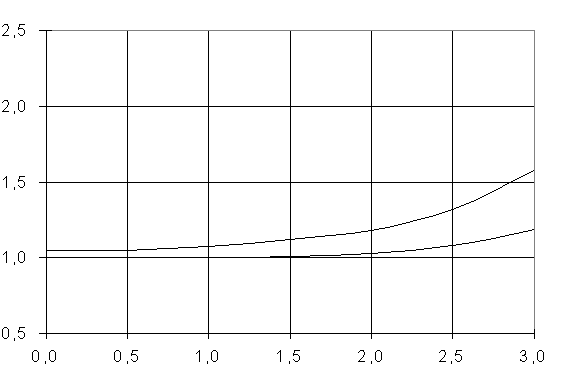
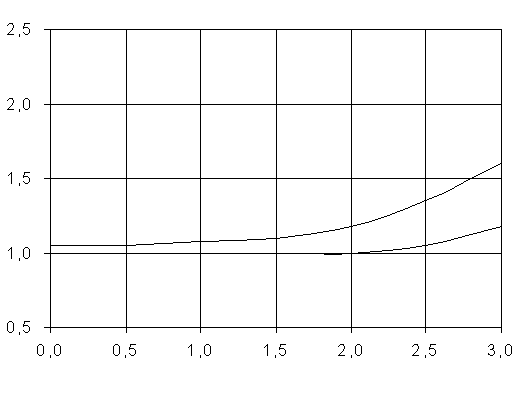
Полученные результаты представлены в таблице 1 и на графиках (рисунки 2-6).

Причем в таблице 1 даны результаты для частного случая, когда логарифм отношения модулей упругости жесткого слоя и заполнителя равен двум [4].

Таблица 1

Прогибы и нормальное напряжение центральных точек слоистых пластин

Количество слоев	двухслойная	трехслойная	Четырех-слойная	пятислойная	семислойная
WЕж.с/100qH	1,831	0,563	1,037	0,641	0,601
σ11/10q	38,58	20,57	40,10	42,11	35,27

Двухслойная Трехслойная

h₁ = 0,8Н; h₂ = 0,2Н; h1 = 0,075Н; h2 = 0,8Н;

Е_ж.с. = 700 МПа; Е_ж.с./Е_зап = 100 (а) h3 = 0,125Н (б)

Четырехслойная Пятислойная

h₂ = h₄ = 0,1Н; h1 = h5 = 0,05Н; h2 = h4= 0,4Н

h1 = h3= 0,8Н (в) h3 = 0,1Н (г)

Семислойная

h₁ = h₃ = h₅ = h₇ = 0,05Н;

h₂ = h₄= h₆ = 0,266Н (д)

Рисунок 1- Поперечные сечения слоистых пластин

0

0

Рисунок 2 - Относительные прогибы и напряжения в двухслойной пластине

0

0

Рисунок 3 - Относительные прогибы и напряжения в трехслойной пластине

0

0

Рисунок 4 - Относительные прогибы и напряжения в четырехслойной пластине

0

0

Рисунок 5 - Относительные прогибы и напряжения в пятислойной пластине

251675648

0

Рисунок 6 - Относительные прогибы и напряжения в семислойной пластине

Анализируя результаты можно сделать следующие выводы:

- Чем больше жестких слоев в пластинах с одинаковым расходом материала, тем жестче становится пластина [5].

- Выгодным по прогибам оказался случай трехслойной пластины, когда верхний жесткий слой в два раза превышает по толщине нижний жесткий слой.

- Чем больше разница в модулях упругости жестких слоев и заполнителя, тем больше разница между результатами, полученными по предлагаемым соотношениям и по классической теории.

Список литературы:

1. Юнусов А.Ш. Изгиб слоистых пластин с заполнителем //Изв.ВУЗов Строительство и архитектура. –1976. -№4.

2. Карасев С.Н. Задача изгиба прямоугольной ортотропной многослойной пластины // -Казань, 1980. –с.6 . Деп. в ВИНИТИ 4.08.80, №..

3. Маличенко С.А., Прусаков А.П. Об одной уточненной теории изгиба слоистых пластин //Изв. ВУЗов. Строительство и архитектура. -1982. -№8.-с.39-42.

4. Касимов А.Т. Алгоритм расчета многослойных ортотропных пластин в уточненной постановке // IV Междунар. конф. Наука и образование – ведущий фактор стратегии «Казахстан – 2030», посвящ. 10-летию Независимости Казахстана. Тез. докл.: - Караганда: КарГТУ, 2001. – с. 22-24.

5. Касимов А.Т. Расчет многослойных ортотропных прямоугольных пластин несимметричной структуры с произвольным закреплением на контуре // Пластины и оболочки: Тр. КарПТИ. -Караганда, 1992.