Горбушина А.Б., Сохацький А.В.

Академія митної служби України

МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ТРАНСПОРТНИХ ПОТОКІВ НА ОСНОВІ ГРУПУВАННЯ ПЕРЕХРЕСТЬ

Останнім часом на багатьох магістралях та в великих містах практично вичерпані ресурси можливого екстенсивного розвитку транспортних мереж[1]. Тому особливо важливу роль має оптимальне планування транспортних систем, покращення організації руху, оптимізації системи маршрутів транспорту. Розв’язування таких задач неможливо без математичного моделювання транспортних потоків.

Створення єдиної, універсальної моделі транспортних потоків це складне і важкоздійсненне завдання, оскільки кожне регульоване перехрестя міста індивідуальне і характеризується властивими тільки йому геометричними параметрами, забудовою зони перехрестя і інтенсивністю руху пішохідного та транспортного потоків, тобто класифікаційними ознаками, які однозначно його визначають. Варто зазначити, що перехрестя можна характеризувати за класифікаційними ознаками, які мають близькі значення. Зважаючи на це, можна провести класифікацію перехресть, де кожному класу буде належати свій набір класифікаційних ознак, які будуть відрізняти його від інших класів[2].

Розробка математичної моделі, яка буде змінюватися в залежності від класу перехрестя дозволить більш точно моделювати транспортні потоки та запобігти побудові безлічі «моделей одного перехрестя».

Всі перехрестя розбиваються на два великі класи, що відрізняються між собою конструктивними особливостями: перехрестя-перетини і перехрестя-примикання, для кожного з яких класифікація проводиться окремо.

При групуванні перехресть по класам виділяються два підходи:

1. Розподіл перехресть по визначеним групам. Заздалегідь відома кількість класів перехресть і треба визначити до якого класу найкраще віднести дане перехрестя, щоб точніше його змоделювати;

2. Формування груп перехресть на основі аналізу їх сукупності. В цьому випадку не вказані чіткі межі кожного класу, а також не відомо заздалегідь скільки класів варто виділити в досліджуваній сукупності перехресть.

так

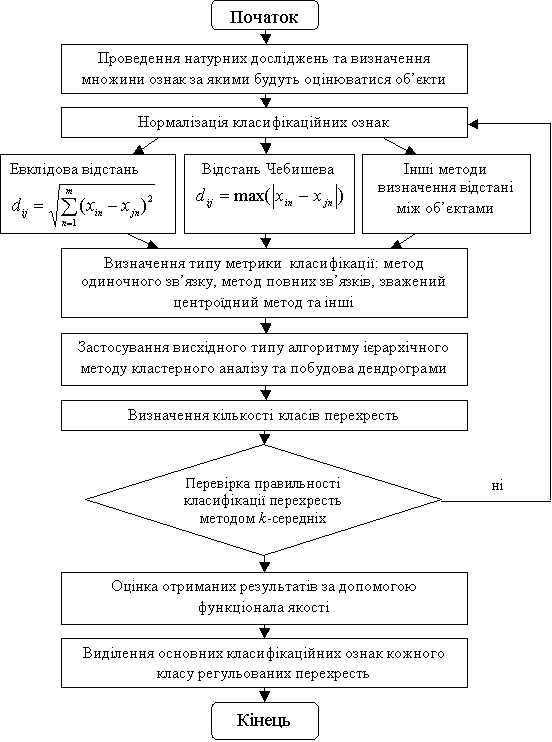
Рис. 1. Алгоритм методу формування груп перехресть на основі аналізу їх сукупності

При побудові математичної моделі пропонується скористатися другим методом, алгоритм якого зображений на рис.1. Після отримання і аналізу результатів,слід провести корегування вибраної метрики та методу визначення відстані між об’єктами до отримання оптимального результату.

Пропонується математична модель для розрахунку транспортного потоку заснована на гідродинамічній аналогії. В основі її лежить виконання законів збереження маси потоку і кількості руху потоку. У випадку одномірної системи координат система диференціальних рівнянь матиме вигляд:

,	(1)
,	(2)

де r - густина потоку, v - швидкість потоку, t – час.

В даній моделі функції і будуть змінюватися в залежності від класу, до якого відноситься модельоване перехрестя, що дозволяє більш точно до реальності описати дорожню ситуацію на даному перехресті.

Висновок. Розроблено алгоритм класифікації регульованих перехресть за класами. На основі цього пропонується математична модель транспортних потоків з використанням гідродинамічної аналогії. Запропонована модель дозволить більш ефективно проводити математичне моделювання великих транспортних систем через використання шаблонних моделей.

Література:

1. Семенов В.В. Математическое моделирование динамики транспортных потоков мегаполиса / Семенов В.В. - М., 2004. - 44 с. : ил. - (Препринт № 34, Москва, 2004 / Институт прикладной математики им. М.В. Келдыша).

2. Тарасов О.В. Методика анализа и классификации регулируемых перекрестков городских улиц / О.В. Тарасов, С.Н. Корнилов // Современные проблемы транспортного комплекса России. – 2013. - №4. – С. 156-163.